Steerable Gaze Control for a
Video-based Virtual Surveillant
|
|
|
Department of Computer Sciences University of Wisconsin-Madison 1210 West Dayton Street Madison, WI 53706-1685 Telephone: 608-262-1965 Fax: 608-262-9777 E-mail: dyer@cs.wisc.edu Web: www.cs.wisc.edu/~dyer
In order to accomplish this objective, we are developing methods for rapidly combining a set of images of a real environment. Video is used as a source of multiple views, in general taken by multiple cameras that are widely distributed around the environment. Output is a set of images to be viewed by a person or used as input to other image understanding algorithms. For both visualization and further processing we are focused on producing photorealistic images of novel views and smooth sequences of views. Thus the main emphasis is on image appearance, not surface reconstruction or model building.
In each of the above tasks the raw sensor data may not be well matched with its intended use. Different tasks require different views of a scene, and so the "optimal" views for a particular task may not have been captured. Also, a sensor may be time-shared for multiple uses in a single mission, e.g., when slewing between multiple targets, and interleaving target tracking with systematic scanning of the environment. For these reasons it is advantageous to synthesize a virtual video tuned to the operator's viewing preferences and task-specific targets and activities, thus enhancing capabilities for monitoring and comprehending areas of interest and assessing objects' dispositions.
The following figure shows the result of view morphing between two input images (left and right) of an object taken from two different viewpoints. The middle image was synthesized by our view morphing algorithm. You can also view a sequence of in-between views (184K MPEG), showing how the impression of smooth motion in depth is created by physically moving a virtual camera.
| Input View 1 | Synthesized View | Input View 2 |
|---|---|---|
 |
 |
 |
The example shows that our approach can synthesize new views of comparable photorealistic quality to the original images. It should be noted that, since view morphing assumes scene points are visible in both input images, some features near the edges of the example fade in or out because they only appear in one of the two input images. Also, note that in the example no special processing has been done to account for moving objects. In the original scene there is a vehicle moving on the road, so its position changes between the two input images. The results here show the vehicle fading in and out of the two positions.
While the synthesized view in the example above is not dramatically different from views in the original video sequence, this is not a restriction on the method; view morphing can potentially generate views that vary significantly from any view in the original video.
|
Two resolutions of Mona Lisa <--> Mona Lisa reflection:
|
The following examples show some early results of this approach.
| Input View 1 | Synthesized View | Input View 2 |
|---|---|---|
 |
 |
 |
| Input View 1 | Synthesized View | Input View 2 |
|---|---|---|
 |
 |
 |
| Input View 1 | Synthesized Movie | Input View 2 |
|---|---|---|
 |
 |
 |
We are developing a new approach called Voxel Coloring that reconstructs the "color" (radiance) at surface points in an unknown scene. Initially, we assume a static scene containing Lambertian surfaces under fixed illumination so the radiance from a scene point can be described simply by a scalar value, which we call color.
Coping with large visibility changes between images means solving the correspondence problem between images that are very different in appearance--a very difficult problem. Rather than use traditional methods such as stereo, we use a scene-based approach. That is, we represent the environment as a discretized set of voxels, and use an algorithm that traverses these voxels and colors those that are part of a surface in the scene. The advantage of this approach is that simple voxel projection determines candidates corresponding image pixels. A difficulty is that a given image pixel may not correspond to a particular projecting voxel if there is a closer voxel occluding the projecting voxel. For example, in the figure below the red voxel in the scene projects into the first and third images but not the second, because the blue voxel occludes it.
To solve this visibility problem we introduce a novel geometric constraint on the input camera positions that enables a single visibility ordering of the voxels to hold for every input viewpoint. This ordinal visibility constraint is satisfied whenever no scene point is contained within the convex hull of the input camera centers. Below are shown two simple camera configurations that satisfy this constraint. The left configuration shows a downward-facing camera that is moved 360 degrees around an object. The right configuration shows a rig of outward-facing cameras that are distributed around a sphere.
 |
 |
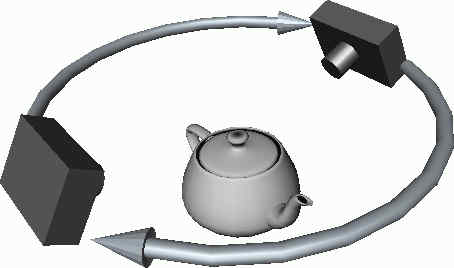Scene reconstruction is complicated by the fact that a set of images can be consistent with more than one rigid scene. Determining a scene's spatial occupancy is therefore an ill-posed problem because a voxel contained in one consistent scene may not be contained in another. On the other hand, a voxel may be part of two different consistent scenes, but have different colors in each. To cope with this problem we say a voxel V is color invariant with respect to a set of images if, for every pair of voxelizations S and T that contain V and that are consistent with the images, we have color(V, S) = color(V, T). Using this invariant, we define a voxel coloring of a set of images to be the maximally consistent coloring.
We can now define the complete voxel coloring algorithm as:
S={} /* initial set of colored voxels is empty
for i = 1 to r do /* traverse each of r layers
foreach V in the ith layer of voxels do
project V into all images where V is visible
if sufficient correlation of the pixel colors
then add V to S
The original Voxel Coloring algorithm was designed for static scenes. Thus producing output quickly was not a priority. To use Voxel Coloring with dynamic scenes several key elements have changed from the original approach. Algorithmically, Voxel Coloring has been recast to take advantage of spatial coherence and temporal coherence. Experimentally, the amount of input data has been reduced significantly. Together, these changes allow us to contemplate implementing Voxel Coloring in real-time on conventional workstations.
The most significant change has been the development of a coarse-to-fine/multiresolution approach to Voxel Coloring which speeds up performance dramatically.
Octree methods are common in coarse-to-fine processing of volumes. We a similar technique for voxel coloring. By decomposing large voxels into smaller voxels, and then coloring the subdivided set of voxels, computation can be focuses on significant portions of the scene.
Because Voxel Coloring depends on statistical methods, a direct decomposition does not work correctly. Voxels that may appear empty at one resolution, could contain subvoxels which should be colored at a higher resolution. This problem is illustrated in the figure below:
To compensate for the abundance of false negatives, the algorithm performs a nearest neighbor search to augment the set of voxels already colored. Such a search relies on a high degree of spatial coherence. In particular, it is assumed that all small details (high spatial frequency) occur close to the details which can be detected at coarse resolution. The figure below illustrates the augmentation process through one iteration.
Depending on the final resolution of the scene, speedups can vary from 2 to 40 times that of the original algorithm. The higher the final resolution the greater the speedup. The scene being colored consisted of eight images radially placed around the figure. The image resolution as 640x480. The images were manually segmented.
 |
The figure on the left illustrates the coarse-to-fine process as resolution increases from 32x32x32 to 256x256x256, doubling at each iteration. In the graph to the right the performance gain for coarse-to-fine processing is illustrated. Also included are timings for prewarping the image to eliminate radial distortion. |  |
To investigate dynamic scene processing, a staging area was built for data capture. Four cameras were used to collect the data. Each camera was mounted at a corner of the area, and was calibrated using the planar implementation of Tsai's algorithm. The walls of the staging area were then covered with blue matte paper to facilitate automatic segmentation. Scene reconstructions were then created serially off-line and redisplayed as a 3D movie. Finally, a version of Voxel Coloring which takes advantage of temporal coherence was developed. The whole process is illustrated in the mpegs below. Dynamic Voxel Coloring is described below.
 |
The input sequence was made up of 16 frames taken from four cameras. The cameras were place near the ceiling in the four corners of the room. The background was covered with blue matte paper to fascilitate segmentation. The resolution of the input images was 320x240. This mpeg shows the stream of input from each camera in turn. |
 |
Voxel Coloring makes use of occlusion information which is built up during scene traversal. This mpeg shows how a particular image is projected onto each layer in turn. Note that the occluded pixels in the image are colored black as the mpeg progresses. Occluded pixels have been accounted for in scene space and cannot contribute further to the reconstruction. |
 |
Static colorings were then created from each of the 16 sets of input frames. This mpeg shows the static coloring with a scene resolution of 256x256x256 voxels. Notice that the reconstruction is hollow. Also note that the photo realism is limited by the resolution of the input images (for example the head was roughly 15 high). |
 |
This mpeg displays the colorings in sequence. The motion of the subject over time adds a great deal of realism to the visualization. (smaller movie) |
 |
The final mpeg shows the voxel coloring algorithm running on a sequence of frames while displaying the output interactively. Each 3D frame is reconstructed in about a half a second on an SGI O2 R5000. To achieve this real-time performance the resolution of the scene has been reduced to 64x64x64 voxels. |
Last modified: 2 November 1999