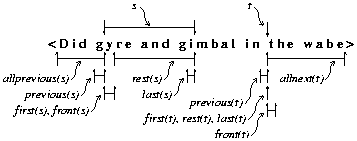27 February 1990
Programming Language Support for Multi-Media Strings with an Algebra
for Subsequences
-
Wilfred J. Hansen
Information Technology Center
Carnegie-Mellon University
Pittsburgh, PA 15213
-
Abstract. String constants and expressions are a basic data
type in most programming languages, but these facilities have not yet
evolved to cope with today's rich range of string contents: typographic
information, letters from non-English alphabets, and embedded pictures,
spreadsheets, and other objects. This paper catalogs the options for
string facilities in programming languages and presents a new algebra
for subsequences that supports string operations. With it programs
can directly refer to any subsequence of a string or other sequence.
This is especially natural for passing substrings to functions and
returning results; for instance, a pattern matching function can return
a single substring value from which the caller can access both the
string that was matched and its surrounding text. Examples are given
in Ness, an experimental language incorporating the algebra.
Early computer users were lucky if their hardware printed strings of
digits. Soon, however, computers could print UPPER CASE text, then
lower case, and eventually all of ASCII as well. Programming languages
have advanced to this point, but now computers are called on to process
and print multi-media text containing letters from other alphabets,
font changes, typographical instructions, and even embedded objects
such as drawings, images, graphs, tables, or entire applications.
For instance, this paper--diagrams and all--has been created as one
file with various embedded objects using the ez text editor component
of the Andrew ToolKit[Morris, 1986; Palay, 1988]. Other systems or
file formats that support multi-media text include ODA [ISO, 1988;
Sherman, 1990], Interleaf [Morris, 1985], and Diamond [Thomas, 1985].
This paper tries to answer the question: "What should string operations
look like in programming languages designed to deal with multi-media
text?" Certainly it should be possible to have such text in program
constants, but what else is necessary? In many languages strings are
treated as arrays of characters. Is this still appropriate when an
element of a string may be a picture? Is there a suitable alternative?
For a language that supports multi-media text--we argue below--the
appropriate alternative to arrays of characters is a new algebra: a
data type with an associated set of operations. For each value in
the data type, there is an underlying base sequence of objects;
when they are all characters, the base is just a character string.
Base sequences are not themselves values, however; instead, a value
is a reference to a contiguous subsequence of a base and many such
values may refer to the same base. The operations of the algebra take
one or two such subsequence reference values and produce related references
to the same base. Indeed, it will turn out that the operations of
the algebra are sufficient to compute every subsequence of the base.
To avoid confusion, let me point out here that the algebra is defined
informally in this paper; the formal definition is in [Hansen, 1989a].
In particular, this is not a paper utilizing an algebraic or denotational
semantics approach to define a data type. Instead, our concern here
is to examine multi-media strings in general and a particular algebra
that seems to offer potential as a component of any programming language.
Examples are given in the Ness programming language [Hansen, 1989b;
Hansen, 1990], which is one implementation of the algebra. It has
also been implemented in the cT system for development of educational
material [CDEC, 1989].
The first two sections define language alternatives for string processing
and review how they are met by existing languages. The new algebra
is introduced in the third section and additional aspects are covered
in the next three. Section 7 presents an extended example, while Section
8 discusses implementation issues. The final section reviews the alternatives
for language design and discusses which choices are appropriate for
which types of language.
1. Requirements
String facilities in programming languages can be measured against
many criteria, including the following. In the section after this
one we will evaluate some popular languages against these criteria.
Unbounded Strings. A number of languages require that the maximum
length of string values be specified when the program is written.
Other languages provide Unbounded String values, the length
of which is managed dynamically at run-time. Bounded values may be
appropriate for low-level languages, such as those in which to write
support software for Unbounded Strings. However, bounded strings either
force the programmer to balloon the program with defensive code or
tempt the programmer to take short cuts with the attendant risk of
bugs. Indeed, one of the system loopholes exploited by Robert Morris's
Internet worm was code that read an unbounded string into a bounded
area. [Spafford, 1989]
Multi-media Text. The impetus for our reexamination of string
processing is the requirement that strings be able to encompass all
the possibilities for modern text. We call this Multi-media Text,
though we mean it to refer not only to embedded objects, but also to
typographic information and non-English letters. In a systems programming
language it is appropriate that the programmer deal with strings at
a low level; many languages treat strings as an array of characters
with one character per byte. For higher level programming, it is more
convenient if strings can be dealt with as they appear on paper; the
assumption of one byte per character may be totally inappropriate because
there may be more than 256 distinct characters in a text or document.
{Of course, with some sacrifice of readability we could insist that
the user encode some characters with escape sequences like \(bs. (sic)}
Substring References. Given a string value, a substring is
a contiguous sequence of some or all of its characters. A substring
value can be implemented as a new string value consisting of a copy
of the sequence, or it can be a Substring Reference, a value
that refers to the sequence in its place within the original base value.
A strategy of implementing all substring values as references has
several important advantages:
-
o Consider writing a function to search a string for some particular
pattern, say the first capitalized word. What should the function
return? To return just a copy of the matched word is unfortunate because
it does not say where the match occurred; there would be no way, for
example, to check preceding punctuation. But to return just the location
of the word does not give the full word. Commonly, such functions
have an additional argument to which the substring length is assigned
by the function, an awkward arrangement at best, and one that is avoided
if the function returns a reference to the substring in its original
location.
o A common alternative to treating substring references as values
is to treat them as integers that refer to locations within strings.
This is a common source of error when there is confusion over whether
a particular variable refers to a character position or the position
between two characters. Other errors arise from failing to recognize
that a substring of length n extends from position p
to position p+n-1, not to p+n.
It seems preferable to refer to substrings directly.
o When Substring References are available, they can be implemented
in a natural way as first-class objects, suitable for assignment to
variables, passing as arguments, and returning as values. When integers
are used instead and a value is returned through a parameter, it may
not be possible to conveniently nest function calls passing the result
of one function as the argument to another.
o With Substring References there is no need to copy the text of the
string to do assignment, pass values to a function, or return values
from a function. For long strings, the resulting elimination of string
and descriptor allocations can be a significant saving; the experiment
reported below showed that immutable strings degraded performance by
a factor of 4.6 in one case and 6.4 in another.
o To implement Multi-Media strings, it may be useful to have differing
numbers of bytes for the representation of different string elements.
Substring reference values capture this naturally: all access to the
string is via references thus obviating the need for concern with the
actual number of bytes in the underlying representation. With integer
indices, each access to the string would conceptually have to count
forward from the first character; hints and other data structures
might not suffice because the integer value could have been computed
by any arbitrary computation.
Please note a distinct difference between substrings implemented with
copying and substring reference values: two substring references with
the same contents are not necessarily isomorphic; they may be at different
positions or in different bases. In particular, empty substrings are
not necessarily isomorphic.
Once substring reference values are recognized, it becomes possible
to define:
An Algebra for Subsequences. An algebra is a set of values
and a set of operators closed over those values. For a substring algebra
the values are the set of all references to substrings. The unary
operators of the algebra accept one substring on a base and return
another defined relative to the argument. Binary operators accept
two substring references and compute a third based on the arguments.
Since the base values may be not only character strings but also sequences
of objects, it seems appropriate to call it an Algebra for Subsequences.
A candidate algebra is described in Section 3.
Concatenation. The essential operation for constructing new
string values is Concatenation; two strings--or substrings referred
to by reference--are arguments and the result is a single string consisting
of a copy of the first followed by a copy of the second. Some languages
which do not offer concatenation provide instead an operation to append
the value of one substring at the end of a string value. If the language
also has bounded string values, the result is expected to meet the
bound of the destination string.
Pattern Matching. The obverse of concatenation is dissection
of a string to find parts of interest. A desired part may be as simple
as an exact match for some string or as complex as the next assignment
statement in a program text. In languages without Pattern Matching
the programmer must write a search as a loop which examines each character
in turn. With pattern matching the programmer writes a pattern expression
which is executed by automatically scanning the subject string to find
one or more instances of the desired substring. Patterns are compatible
with languages having Substring References because the result of a
pattern match can be a reference to the entire matching substring.
Mutability. The final consideration in design of a string facility
is the degree to which string values once created can later be modified.
Several choices are possible. For many applications it is entirely
reasonable that string values be immutable; as the program
generates new values it constructs them by concatenation of other strings
to form new strings. If the generated strings are long, however, it
may be preferable to append new values to the end of existing
ones rather than recopy the strings. After the append, any substrings
of the modified value still refer to the same places they did before
because the base string has changed only after the position referred
to. If their location was found via a string search, there is no need
to repeat the search to refind them.
Modification by appending strings may be insufficient, however, to
support some interactive applications. In a text editor for instance,
a string the size of a file is being editted and changes may be made
at any place. Not only is it costly to copy the entire string for
each modification, but there may be substring references to portions
of the string which would have to be recomputed somehow for the new
string. In such cases it is preferable to be able to replace
a portion of a base string with new contents; moreover, replacement
with an empty string does a deletion and replacement of an empty substring
does an insertion. As the modification is made the system can automatically
adjust other substring references so they continue to refer to their
original targets.
A few languages support a limited form of mutability by replacement;
they allow the program to replace a given substring with another substring
only if the replacement is the same length as the replaced text. This
is not a particularly common operation in string processing and cannot
be considered an acceptable form of mutability. Indeed, with multi-media
text a replacement value may have the same number of characters but
may actually occupy a different number of bytes due to different code
lengths for different sorts of characters or objects.
The choice among the three forms of mutability has a major impact on
the implementation of the language. The substring algebra is defined
without mutability in Section 3 and mutability is discussed in Section
6.
2. Existing Languages
Since most programming languages support strings to some degree, we
cannot review them all here; instead we examine the fourteen well-known
and representative languages listed in Tables 1 and 2. In some cases
the discussion is with respect to the language as augmented by standard
libraries commonly provided with implementations.
The tables review the languages for the degree to which they meet the
criteria of Section 1. An entry of dash indicates the language makes
no attempt to meet the criterion; YES means the language fully meets
the criteria; intermediate cases are coded with yes-x if they
provide a modest approximation to the criterion or with just x
if they do not meet the criterion but have some partial alternative;
see the Notes to Tables for the various values of x.
|
| Fortran
| Cobol
| Basic
| Algol-68
| C
| Pascal
| Ada
|
| Unbounded
| -
| -
| yes-a
| YES
| yes-b
| -
| -
|
| Multi-Media
| -
| -
| -
| -
| -
| -
| -
|
| Substr Refs
| j
| k
| j
| j
| -
| -
| j
|
| Algebra
| -
| -
| -
| -
| -
| -
| -
|
| Concat
| yes-c
| -
| YES
| YES
| -
| -
| yes-c
|
| Patterns
| -
| l
| l
| -
| l
| -
| -
|
| Mutability
| m
| yes-d
| YES
| m
| yes-d
| m
| m
|
-
Table 1. String facilities of popular low-level languages.
See Notes to Tables. The languages are defined by [FORTRAN77: ANSI,
1978; COBOL 1985: ANSI, 1985; Advanced Basic: Microsoft, 1981; Algol-68:
van Wijngaarden, 1976; C: Kernighan, 1978; Pascal: Wirth, 1974;
Ada: DOD, 1980].
|
| Snobol4
| Icon
| Lisp
| REXX
| PostScript
| Hypertalk
| Modula-3
|
| Unbounded
| YES
| YES
| YES
| YES
| yes-b
| YES
| YES
|
| Multi-Media
| -
| -
| yes-f
| n
| -
| -
| -
|
| Substr Refs
| -
| j
| yes-f
| j
| yes-e
| -
| yes-e
|
| Algebra
| -
| -
| -
| -
| -
| -
| -
|
| Concat
| YES
| YES
| YES
| YES
| -
| YES
| YES
|
| Patterns
| YES
| yes-g
| l
| yes-h
| l
| -
| -
|
| Mutability
| YES
| YES
| m
| -
| m
| yes-i
| -
|
-
Table 2. String facilities of some other languages. See Notes
to Tables. The languages are defined by [SNOBOL4: Griswold, 1971;
Icon: Griswold, 1983; Common Lisp: Steele, 1984; REXX: IBM, 1987;
PostScript: Adobe, 1985; Hypertalk: Atkinson, 1987; Modula-3: Cardelli,
1988].
Notes to Tables
-
-
blank: The criterion is not met by the language.
YES: The language fully meets the criterion.
yes-a: In some implementations of Basic strings have a very small maximum
length.
yes-b: Strings of any length can be created, but the program must explicitly
perform the storage allocation operation.
yes-c: If a concatenation result is assigned to a variable, it must
fit into the space allocated for that variable.
yes-d: It is possible to replace a substring with another of the same
length, it is also possible to append to a string value.
yes-e: There are substring reference values, but they do not provide
access other elements of the base string.
yes-f: In LISP, strings cannot have Multi-Media or Substring References,
but the more general "vector" type can have both.
yes-g: In Icon patterns are constructed by flow of control through
pattern matching primitives.
yes-h: REXX patterns are limited to a few of the most useful cases.
yes-i: In Hypertalk replacement of a character, word, or line is simple,
but replacement of a sequence requires a loop.
j: Substring expressions are provided, but their value is the sequence
of characters, not a reference to the sequence.
k: In addition to property j, COBOL allows a name to refer to a portion
of a statically allocated string.
l: There is an operation to find one string in another.
m: It is possible to replace a substring with another of the same length.
n: REXX strings may contain non-English letters.
Table 1 lists low-level languages in the tradition of Fortran and Algol.
Most of these languages treat strings as arrays of ASCII characters
so it is not surprising that they meet few of the criteria; indeed,
the entire table has only four unqualified YES's. None of the languages
provide Multi-media text, Substring References, or a Subsequence Algebra.
Those languages which do have substring expressions define them to
produce the value of the substring rather than a reference to it.
In this model, when a substring is passed to a function the receiver
can access its value but cannot scan forward--or backward--to find
other parts of the underlying string.
The languages in Table 2 are at a higher level than those above and
are correspondingly more supportive of strings. Note, however, that
just like the first table, no listed language provides unqualified
support for Multi-Media Text, Substring References, or a Subsequence
Algebra.
Although few languages satisfy the various criteria and none satisfy
them all, it is not the case that these are poor languages. Most are
excellent tools within their own design space. Clearly, however, none
is ideal for working with multi-media text.
3. An Algebra for Subsequences
An algebra is a set of operations closed over some domain called its
"sort". When programming languages treat strings as arrays of characters
with integers to refer to substrings, they utilize a more complex,
multi-sorted algebra combining both strings and integers. It will
be our contention in this section that all present string operations
and some new, desirable ones can be defined with a single-sorted algebra
over the domain of substring references. First, some definitions:
-
A sequence is an finite, ordered collection of elements, each
of which is a character or object. Before each element and after the
last is a "position".
A subsequence reference, or subseq, is a triple consisting
of a pointer to an underlying base sequence and a first and
last position within its ordered collection.
A subseq that refers to a subsequence of length zero will be called
empty.
When the sequence referred to by a subseq is primarily characters it
will be common below to talk of it as a substring.
Before starting on the operators of the algebra, we must redefine traditional
string expressions in terms of subseq values. This discussion will
also serve to introduce the notation to be used later; a notation which
is close to the Ness language [Hansen, 1989b]. However, the algebra
itself is in no way peculiar to Ness; it can be incorporated in many
different programming language models.
Character and string values are not required. Instead of a
character value we use a subseq referring to a single character; instead
of a string value we use a subseq referring to an entire base string.
Declarations are written with the declarator first:
- subseq m, s, t
Each of m, s, and t refers to a substring.
(In older implementations, the typename `marker' was used instead
of `subseq.')
String constants are bounded by quotation marks:
-
"
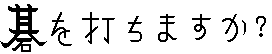 is Japanese for Do you play go?"
is Japanese for Do you play go?"
The semantics of a string constant are that it returns a subseq which
refers to the entire constant. This example contains both italic text
and a raster image of Japanese characters; in principle it could contain
the Japanese characters themselves. A constant is an immutable value.
Functions. Subseq values may be passed as parameters or returned
as values. Here is a definition of a function with three arguments
that returns the second as its value:
- function f(r, q, integer i)
return q
end function
The default type for parameters and function return value is subseq.
Parameters are call-by-value, but replace modifications to
a parameter subseq will affect the same base on which the argument
subseq resides. Functions are called by listing actual arguments in
parentheses after the function name:
- f(m, "constant", 3)
If the value returned from a function is a subseq value, it continues
to refer to a substring of whatever is the base of the expression.
In particular, if the base sequence was created within the function,
it will now be accessible outside the function.
Assignment of subseq values is assignment of references:
- s := "new value"
p := m
assigns to s a reference to the entire constant substring
"new value" and to p a reference to the same substring and
base as m.
Comparison and printing. When two subseq values are compared,
the elements of the referenced substrings are compared; the comparison
ignores the rest of their bases. (An implementation must choose some
collating order for non-character objects.) Similarly, printing a
subseq value prints only the referenced portion of the base. Note
that this differs from assignment where the base is implicit in the
assigned value.
Concatenation. When two subseq values are concatenated the
result is a brand new base string. We write a tilde for concatenation;
the code
- s := "new value"
p := s ~ "!"
will assign to s a reference to "new
value"
and to p a subseq value referring to the entire base of
a new string having "new value!"
as its contents.
String input. The function read(filename)
reads the named file and returns a subseq value for its entire contents.
Thus, there are three ways to get new string base values: constants,
concatenation, and string input.
Pattern matching. The result of a pattern match operation is
a subseq value referring to the entire substring which has matched
the pattern. The next section will cover the pattern functions that
are currently implemented in Ness.
Primitives for the Subsequence Algebra.
With the above reinterpretation of string operations as subseq operations,
we now turn to the operations of the subsequence algebra. Four primitive
functions have proven to be a simple and convenient basis for the algebra:
start(), base(), next(), and extent(). These are illustrated in Figure
1. We will show in Section 8 that start()
can be implemented in a single instruction. Other subseq operations
can be implemented with similar brevity.
-
Figure 1. The four primitive functions. The base string is
shown between < and > with three typical subseq values above it. The
subseq values below the base show the result of applying the primitive
functions to m, n, and p. For an
empty subseq the value is shown as a vertical arrow; for a non-empty
subseq the value is shown as two half arrows joind with a horizontal
line.
start(x) - The value of start(x)
is a subseq refering to the position at the start of the value referred
to by x. Suppose x refers to the substring
cde of the value abcdefg, then the value of start(x)
is a subseq for the empty position between b and c and on the same
base string as x.
base(x) - Returns a subseq for the entire base string of which
x refers to a part. Suppose again that x refers
to the substring cde of the value abcdefg, then the value of base(x)
is a subseq referring to the entire value abcdefg.
To get an empty subseq at the beginning of the underlying base string
for x, we can write start(base(x)).
The opposite composition, base(start(x)),
returns exactly the same value as base(x)
because x and start(x)
both refer to the same underlying base string.
next(x) - This function returns a subseq for the character
following x. When x is cde in abcdefg, the
value of next(x)
is a subseq for f. If the argument x extends all the way
to the end of its base string, then next(x)
returns an empty subseq for the position just after x.
Now we can write expressions for more interesting substrings relative
to a given subseq x. The element first after the beginning
of x is front(x) = next(start(x))
because start(x)
computes the empty subseq just before the first character and next()
computes the character just after its argument. Similarly, the second
element after the beginning of a given subseq x is next(next(start(x)))
and the first character of the base is next(start(base(x))).
extent(x, y) - Computes a subseq from two other subseqs on
the same base. The new subseq value extends from
the beginning of the first argument, x
to
the end of the second argument, y.
For instance, suppose a base string is abcdefg and in it x
refers to cde while y refers to bcdef. Then extent(x,
y)
computes a reference to the substring cdef, extending from c at the
beginning of x to f at the end of y. The two
arguments need not overlap or even be contiguous; if x
is bc and y is ef the value of extent(x,y)
is bcdef.
It may be that the first argument of extent()
begins after the second ends. In this case extent()
is defined to return a subseq for the empty position just after the
second argument. Note that this position comes before
the beginning of the first argument. Another possible problem with
the arguments to extent()
is that they may be on different base strings. In this case, the
value returned is a subseq on a unique, immutable base string which
has no characters.
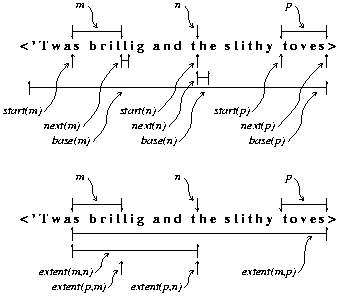
Non-primitive Functions.
With the aid of extent()
we can write expressions for all of the interesting substrings relative
to a given substring. As examples, see Figure 2, which illustrates
the following:
-
-
front(x) = next(start(x)), the element
which starts where x starts (even if x is empty)
finish(x) = start(next(x)), the empty
string at the point where x ends
last(x) =
{exercise to the reader}, the last element in x, or the
empty string if x is empty
previous(x) = last(extent(base(x), start(x))),
the element preceding x
allprevious(x) = extent(base(x), start(x)),
everything before x
allnext(x) = extent(next(x), base(x)),
everything after x
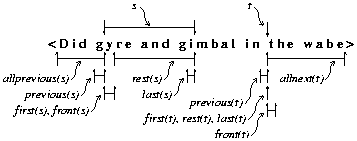
-
Figure 2. Examples of non-primitive functions.
The code for last()
can be written with a loop using next()
to cycle through the elements of x, looking for one, say
t, for which extent(start(next(t)),
start(next(x)))
yields the empty string. This function can be written more concisely
as a recursive function utilizing the rest()
function we define next.
Given a subseq value we may want to process all its elements by processing
the first at each step and then processing the rest. For this purpose
the functions first()
and rest()
are needed, but each must be defined to have the empty string as its
result if the argument is empty. It is convenient to first define
rest()
with the somewhat subtle expression
- rest(x) = extent(next(next(start(x))), x)
The extent()
giving the value of rest()
clearly ends where x ends, as it should. If x
has one or more characters, the first argument to extent()
will have its starting position just after the first character of
x, so the extent returns all of x after its first
character. The subtlety arise when x is empty; in this
case the first argument to extent()
starts at a position beyond the end of the second argument, so the
result is the end of that second argument. But the second argument
is the empty string, x, so the value of the extent is empty
when x is.
We can now compute first(x)
with the aid of rest(); it is the
subseq which extends from the beginning of the original subseq up to
the beginning of the rest(x), in other
words,
- first(x) = extent(x, start(rest(x)))
It may seem inefficient to compute first()
and rest()
so indirectly, but these are just formal definitions in terms of the
four primitives start(), base(),
next(), and empty().
In practice first()
and rest()
are implemented by writing them directly in the low-level language
that implements the primitives.
Necessity and Sufficiency.
The set of primitive functions for an algebra--next, start, base, and
extent, in this case--ought to have the properties of necessity and
sufficiency. The first requires that no function be expressible in
terms of the others and the second requires that the functions be sufficient
to compute all values in the domain of the algebra. Both proofs are
beyond the scope of this paper, but we can give a simple proof of a
form of sufficiency. For more details see [Hansen, 1989a].
Though sufficiency would require us to compute any specified subsequence,
let us instead show how to compute the set of all subsequences
of a sequence; that is, the set is all subsequences that begin at
one position in the sequence and continue to the same or another, later
position. To do something with the generated subsequences, each is
printed as it is computed:
- function printsubsequences(s)
printsubsub(s, s)
if s /= "" then
printsubsequences(rest(s))
end if
end function
function printsubsub(t, s)
print (extent(s, start(t)))
if t /= "" then
printsubsub(rest(t), s)
end if
end function
Careful examination will convince the reader that for an s
of length n the functions will print n+1
empty subsequences, one for each position in s. Of course,
they also print all the non-empty sequences. Both facts can be proven
by beginning with a lemma:
Lemma 1 (Tail Recursion): If P is an operation
and Q is a sequence of zero or more variables each preceded
by a comma, then the function f()
defined by
- function f(x Q)
P(x Q)
if x /= "" then
f(rest(x) Q)
end if
end function
performs P once for each tail of x,
including the final empty subsequence. That is, if x refers
to a substring s1s2s3...sn
of some base then P is executed once for each of
s1s2s3...sn,
s2s3...sn,
s3...sn,
...
sn,
empty string after sn.
Proof: If x is is an empty string, then n
is zero and P is executed once; the then
clause is not executed because x = "".
When n > 0 we argue by induction. A call to f()
evaluates P once for the current value of x
and then calls f
recursively for rest(x). By the definition
of rest, rest(x)
is a tail of x so n is one less and the general
case holds by induction.
Lemma 2: The call printsubsub(s,
s)
prints all subsequences of s that begin at start(s).
Proof: By the Tail Recursion Lemma, printsubsub(s,
s)
executes print(extent(s, start(t)))
for t being each tail of s. This is exactly
the subsets of s that begin at the beginning of s.
Theorem: The call printsubsequences(s)
print all subsequences of s.
Proof: By the Tail Recursion Lemma, printsubsequences(s)
executes printsubsub(s, s)
for each s which begins a tail of the initial s.
By the preceding Lemma, this call prints the subsequences beginning
at each position within s, which is the entire set of subsequences.
In principle we can replace the call on print()
in the above functions with a test to see if we have found a desired
subsequence. Since the iteration will visit all subsequences, we will
eventually find the desired one, if it exists. Thus the primitive
functions of the subsequence algebra are sufficient to compute any
subsequence, at least if it can be described by a predicate.
Are the four primitive functions all necessary? Yes and no. As shown
in [Hansen, 1989a], none can be expressed in terms of the others.
However, there is a smaller--though less convenient--set of primitives
consisting of next()
and extent()
as already defined and a third function we can call startofbase().
In terms of the four primitives, startofbase(x)
would be defined as start(base(x)),
but we can also define base()
and start()
in terms of startofbase(). The computation
of base(x)
is straightforward: set t to startofbase(x),
loop setting t:=next(t)
repeatedly until t is empty, and finally derive the base
as the extent()
from the startofbase(x)
to t. It is trickier to implement start()
in terms of the three primitives; the heart of the solution is to
move an empty subseq through the base sequence one element at a time:
- function start(m)
-
subseq p := startofbase(m)
while extent(p, m) /= m do
-
p := next(p)
p := extent(next(p), p)
-- p is still empty, but is one element further along in m
end while
return p
end function
The algebra with only three primitives is formally simpler than the
one with four. However, the four functions are so much more useful
in practice that it seems preferable to present the algebra in their
terms.
4. Pattern Matching
Pattern matching scans a text to find a substring conforming to some
specified description. With Substring References in the language and
a Subsequence Algebra, the result of a pattern match is a subseq referring
to the substring that matched the pattern. At present, no comprehensive
pattern matching sublanguage has been introduced in the Ness implementation
of the algebra, but the need is apparent and research is scheduled.
What the implementation does provide is a small set of elementary
searching operations that can be linked together to perform more complex
searches. In this respect, the approach is similar to Icon [Griswold,
1983], but has two major differences: failure is not used for flow
of control and the result of an operation is a substring instead of
a numeric position.
The searching operations implemented each have two arguments, a subject
string and a specification. By convention, a non-empty subject
restricts the search to that substring while an empty subject searches
from the subject to the end of the base. Also, by convention, a search
failure is indicated by returning the empty string at the end of the
specified subject. These conventions are related since the end of
the subject argument specifies both the extent of the search and the
value for failure; this relationship has not proven awkward in any
of the many programs written so far.
In the descriptions below, when the pattern specification is pat,
the match must be an exact match, character-for-character; when the
specification is set, the substring supplied is treated as a
set of characters, multiple occurrences within the specification are
ignored.
-
-
search(x, pat)
- looks for the first instance of pat in x.
match(x, pat)
- matches pat only if it begins at start(x).
anyof(x, set)
- finds a single character, the first that is one of the characters
in set.
span(x, set)
- matches all contiguous characters at the beginning of the subject
string which are in set.
token(x, set)
- finds the first substring in x which is composed of characters
from set.
Each of these five pattern functions can be written in terms of the
four primitives of the algebra. The simplest is token,
which depends on anyof
and span:
- function token(x, set)
subseq v := anyof(x, set)
if v = "" then
return v
elif x = "" then
return span(start(v), set)
else
return span(extent(v, x), set)
end if
end function
The trickiest subcase is when x is non-empty and does not
contain a character from set, but is immediately followed
by such a character; without this problem, the function could be written
more simply. The reader is challenged to write the simpler version
of token and also functions for the other four matching functions defined
above.
Earlier we posed the problem of finding the next capitalized word in
some text. With the primitive pattern matching functions we can write
this as:
- function capstart(t)
-
t := token(start(t), letters_all) -- find the first word
while t /= "" do
-
-- t has a word, check its first letter
if search(letters_upper, first(t)) /= "" then
-
-- bingo, the first letter is a capital
return t
end if
t := token(finish(t), letters_all) -- find next word
end while
end function
With the algebra it is natural to find words and check their first
letter. With other languages--such as C--it may be more straightforward
to check each letter in turn to see if it is a capital and the previous
character is not a letter. In the following code we utilize the Andrew
ToolKit (ATK) functions to access the text in order to illustrate what
the program looks like for Multi-Media Text. Note that a third argument
is required in order to return the length of the word we have found.
-
char *
capstart(t, p, n)
-
struct text *t; /* input text */
long p; /* position in t */
long *n; /* return the length */
{
-
long i, t_end = text_GetLength(t);
char c = '\0', prec;
for (i = p; i < t_end; i++) {
-
prec = c;
c = text_GetChar(t, i);
if (isupper(c) && ! isalpha(prec)) {
-
/* found a word */
p = i;
for (i = p; i < t_end; i++)
-
if ( ! isalpha(text_GetChar(t, i)))
-
break;
*n = i-p;
return p;
}
}
return NULL;
}
Notice that both algorithms examine each letter once and a few letters
twice. The version in the algebra examines twice the first letter
of each word. The C version examines twice only those letters which
precede capital letters. The reader may find it instructive to rewrite
the subsequence algebra version to employ the same algorithm as the
C version.
5. Multi-Media Text
As developed so far, the algebra is sufficient for multi-media text
to the extent that constants and data may contain arbitrary elements.
No additional functions are needed to support letters from non-English
languages, although the implementation must be able to read, store,
display, and write them. For typography and embedded objects, further
functions are essential. We describe one possible set here, but have
no evidence to suggest that these are the best choices.
Typography associates with each span of text a "style" in which it is
displayed and printed. The components of a style determine indentation,
font family and size, justification, subscription and other characteristics.
In some systems typography is directly encoded--the style directly
specifies the various attributes of the affected span--while in other
systems the style is indirect--the span is tagged with a name and a
table elsewhere specifies the typographic attributes for that name.
It would be possible to develop an elaborate system of defining styles
and append that to the definition of the substring algebra, but for
simplicity Ness was designed to be independent of the style definition
mechanism. When a program needs a constant specifying a style, a string
in that style is used instead, as in these functions for applying removing,
and testing styles:
-
addStyles(x, styledText)
-- The substring referenced by x is given additional style
attributes as necessary for it to have at least all the styles as the
first character of styledText. For instance, if the substring
is
-
example with italic and underline
and the first letter of styledText is in the helvetica font
family and two points larger, the resulting text will be Helvetica
and two points larger:
-
example with italic and underline
removeStyles(x, styledText)
-- The substring referenced by x is unstyled by removing
from it all styles of the first character of the second argument.
RemoveStyles is not quite the inverse of addStyles. The two statements
- addStyles(x, style)
removeStyles(x, style)
may modify x if it originally had one of the styles that
were added with the addStyles.
hasStyles(x, styledText)
-- The first character of x is checked to see whether
it has all the style attributes of the first character of the styledText.
With the above example as the x and a piece of Helvetica text as the
styledText, the function would yield True,
but if styledText were italic, the function would return
False.
Note that the first two functions define mutations of the base string.
Alternatives could be defined in which each function returns a copy
of its first argument modified in accordance with the second.
In some applications it is desirable to find all the characters in
some given styled substring, for instance, to find the italic word
in the example string above. As a minimum requirement we need a function
to advance through a text returning each span that has a style distinct
from its neighbors. To do this in an iteration, the argument at each
iteration will be the result returned on the previous iteration.
-
nextStyleGroup(x)
-- Scans the base text of x and returns a substring referring
to the next span with a style distinct from x. If a larger
styled span starts at the same place as x, that larger span
is returned. Otherwise the start of the returned value is the next
character in the text which has a style differing from front(x)
and the extent of the returned value is the smallest span of characters
all having the same style.
Utilizing the style functions we can write a function, TofC(t),
to build a table of contents. The argument will be a piece of text
and the result will be a text containing a list of the headers found
within the original text. The basic strategy is to find each style
group in the text and decide if it is a header by examining its style.
We can make an initial attempt like this:
- function TofC(t)
subseq s := nextStyleGroup(start(base(t)))
subseq tc := newbase() -- destination for table
while s /= "" do
if hasStyles(s, "template") then
-- (INCORRECT)
tc := tc~ s~ "\n"
s := finish(s)
end if
s := nextStyleGroup(s)
end while
return tc
end function
Each time around the loop, s has a different style group
and the if-test determines whether that group has the same style as
template, which happens to have the "heading" style. If so, the
group is appended to the accumulating table of contents in tc.
The difficulty with this first version of TofC is that the several
style groups may begin at the same place as a heading. The program
needs to select from them the longest which has the heading style.
The correct version of the function tests each character of the text
to see if it is a heading. (This would be more efficient with some
function similar to span().) We do
this by adding the following in place of the comment "--
(INCORRECT)" above:
- subseq c := first(s)
while hasStyles(c, "template") do
c := next(c)
end while
s := extent(s, start(c))
In this loop c is always a character and the loop continues
until c is not in the heading style. In this case the character
before c was in heading style, so start(c)
is a subseq value at the end of the heading; the heading itself extends
from the beginning of s to just before c.
The reader is invited to consider the set of all possible style operations
and determine which can be implemented with the functions above. It
seems likely that all can be, but a proof of this contention must await
a more formal description of styles. More examples of usage of the
style functions appear in Section 7.
Embedded objects can appear in strings as additional elements; the
raster image of the Japanese characters above is just a single object
between a space and a quotation mark. One alternative choice would
be that objects are "tied to" characters or positions between characters;
this is unattractive because it makes it difficult to deal with having
multiple objects at any given position.
To construct strings with embedded objects, we define concatenation
of a string with an object to produce a new sequence containing the
object. Thus the statements
- object r := new("raster")
raster_Read(r, "/usr/andrew/lib/rasters/fred.raster")
"wjh:" ~ r
produce a sequence of five elements: three letters, a colon, and a
raster object. When a string is printed, objects within it are converted
to their print form, so the above string would print
- wjh:

as you might expect. The same translation to print form is available
as a function so programs can deal with the print form of objects if
necessary.
It is sometimes essential to find objects in strings, so we need:
-
nextObject(x)
-- Searches x for an object and returns a substring value
referring to the single element which is the object. If none is found,
returns the empty string at the end of x. If x
is empty, the search extends to the end of the base.
To extract an object from a string we have:
-
c(x)
-- {"contents-of"} This function examines next(start(x));
if it is an object, the function returns that object, otherwise it
returns next(start(x))
itself, which is a subseq value and not an object.
To transform the system into one with general list, tree, and graph
structures, all we need is some way to store subseq values as objects
in sequences. This cannot be done with concatenation as for the raster
opbject above because concatenating two subseq values is (and should
be) defined to copy the strings the subseqs refer to. So we need just
one more function:
-
obj(x)
-- Returns an object which encapsulates the argument subseq value.
To get a list of subseq values we can write obj(m) ~ obj(p) ~ obj(s),
which produces a three element sequence no matter what the lengths
of m, p, and s.
When extracting a subseq value that was encapsulated with obj(), the
function c() according to its definition above would return an object
which encapsulates a subseq. But since there are no functions which
operate on such values, we extend the definition of c() so that if
the value it would return is an encapsulated subseq it returns the
subseq instead. Thus, whenever x is a subseq value the following three
expressions yield equivalent values: x, c(obj(x)),
c(obj(x) ~ "abc"). However, these values
differ from c(obj(x ~ ""))
because this even though the elements of the returned sequence are
the same as x, they are on a new base created by the concatenation.
6. Mutability
Earlier we defined three levels of mutability for string values: Immutable,
Append, and Replace. The latter two require more operators and more
implementation complexity than the algebra presented so far.
With Immutable strings the implementation of subseq values is
straightforward because base strings are invariant; once created,
a substring value never changes. However, the only way to alter a
string value is to concatenate pieces to make a new one, an approach
which may have some performance penalty for programs which generate
strings for output. Programming convenience can suffer, as well.
When a new string value is created there are no subseqs referring to
its components; if the program has determined a useful set of subseqs
of the old base, their locations will have to be recomputed in the
new one.
The Append level of mutability introduces to the algebra one
new function: append(). This function
has two subseq arguments and modifies the first by inserting at the
end of its base a copy of the second. This level of mutability is
well suited to programs that translate an input into an output because
the output is constructed a piece at a time without the need to copy
the completed portion as a new portion is appended. Subseqs referring
to the completed portion remain undisturbed, so they need not be recomputed.
We write append as
- old-base-variable ~:= substring-expression
The effect of this operation can be considered to be
- old-base-variable := base(old-base-variable) ~ substring-expression
but it must be understood that the concatenation does not copy the
old-base-variable and instead modifies its base.
Replace level mutability provides the operation of replacing
the text referenced by a subseq value with some replacement string.
This is especially useful for interactive applications like text editors
because replacements can be made at any point in a large string without
the requirement of creating a new string. Rather than define syntax
for replace, we write it as a function:
- replace(reference-to-a-substring, replacement-string-value)
Replace(x,r)
modifies base(x)
by substituting a copy of r for the the part of base(x)
referred to by x. It returns a subseq referring to the
newly installed value in its location within base(x).
Since other substring values may refer to portions of base(x),
they must be adjusted so they continue as best they can to refer to
the same text. Adjustment is illustrated in Table 3 and can be described
as if replace(x,r)
inserts a copy of r at finish(x)
and then deletes x. If any other subseq, say M,
begins at finish(x), then the insertion
is not included in M. If any subseq M ends at
finish(x), M is extended
with the insertion only when x is non-empty. Following
these rules, x itself will be updated to include the new
value only when x is non-empty. If x is empty,
its final value will precede the insertion.
-
Replace "efgh" in abcd efgh ijkl with "xyz"
The substring a / bc / defghijkl becomes a / bc / dxyzijkl
The substring a / bcd / efghijkl becomes a / bcd / xyzijkl
The substring a / bcde / fghijkl becomes a / bcd / xyzijkl
< The substring a / bcdefgh / ijkl becomes a / bcdxyz
/ ijkl
The substring a / bcdefghi / jkl becomes a / bcdxyzi /
jkl
The substring abcd / efg / hijkl becomes abcd / / xyzijkl
< The substring abcd / efgh / ijkl becomes abcd / xyz
/ ijkl
The substring abcd / efghi / jkl becomes abcd / xyzi /
jkl
The substring abcde / fg / hijkl becomes abcd / / xyzijkl
< The substring abcde / fgh / ijkl becomes abcd / xyz
/ ijkl
The substring abcde / fghi / jkl becomes abcd / xyzi /
jkl
> The substring abcdefgh / / ijkl becomes abcdxyz /
/ ijkl
> The substring abcdefgh / i / jkl becomes abcdxyz /
i / jkl
Replace empty string between c and d in abcdef with "xyz"
< The substring a / bc / def becomes a / bc / xyzdef
The substring a / bcd / ef becomes a / bcxyzd / ef
< The substring abc / / def becomes abc / / xyzdef
> The substring abc / d / ef becomes abcxyz / d / ef
The substring abcd / e / f becomes abcxyzd / e / f
-
Table 3. The effect of replace() on other subseqs. The replace
performed for each group of lines is shown above the group. Each line
shows an example of some other substring value on the same base and
what its value is after the replacement. The base string is letters
only; the spaces are for readability and the slashes indicate the extent
of the substring values. In general the replacement is made by inserting
the replacement at the finish of the replaced value and then deleting
the replaced value. The <'s mark examples where the "other" substring
ends at the beginning of the replaced string and the >'s indicates
examples where it begins at the end of the replaced string.
After replace() is defined, append need no longer be treated as a primitive
operation. The operation a~:=b
can defined to be
- a := base(replace(finish(base(a)), b))
This definition makes it clear that the value of a is modified by the
append statement. Please review Table 3 to observe that in this case
no existing subseq is modified by the append operation; the relevant
lines are the last two prefixed with "<" in the case where def is empty.
With mutable strings, whether at the Append Level or with Replace,
there is a problem with constants. If a program sets a variable to
a constant and then appends to or replaces a portion of the value,
a constant string base would be modified. One way for a program to
avoid this problem is to copy a constant before using it, as can be
done by concatenation with an empty string. The string expression
- "constant string" ~ ""
always produces a new, mutable string value.
The algebra can be made a little cleaner however if we define a primitive
function,
- newbase()
which returns a unique, newly created, empty, and mutable string base
value each time it is called. With this function we can now redefine
concatenation as a non-primitive operation by saying that the concatenation
a~b
is defined to be
- base(replace(finish(replace(newbase(), a)), b))
In this expression, the argument to finish()
is a mutable copy of a, the tail end of which is replaced
by the outer call to replace. The final call to base()
computes a subseq referring to the entire result of the concatenation.
Mutability of strings complicates all other operations because of the
need to keep track of all substrings on each base in order to modify
them when a replace()
occurs. For strings that are never modified, this overhead is pointless,
which suggests that an implementation might provide two separate classes
of substring value: mutable and non-mutable. A declaration like
- mutable subseq a, b
would declare variables whose values would be guaranteed to be mutable.
A function mutable()
would copy its argument and produce a mutable copy; for special cases
the compiler could optimize calls on this function to produce a mutable
string without copying.
What is the execution penalty for insisting on completely immutable
strings? To try to answer this, I timed various Ness versions of a
routine to copy a string, s, as shown in Appendix A. The
most straightforward copy operation, s~"",
was also the fastest--0.6 seconds. Building the copy one character
at a time with append took longer--4.4 seconds, but was very close
to the time to insert each character in turn with replace()--4.6 seconds.
Both append and replace() are special cases because the implementation
of strings is optimized for multiple modifications at the same point,
so the next test inserted each character at a random position in the
destination; this took considerably longer--11.6 seconds--which is
not too bad considering that over six megabytes were moved to do the
insertions.
With immutable strings, concatenation is the only way to construct
new values. Copying s with concatenation--29.6 seconds--took
more than six times as long as the worst time with replace(). Creating
a randomly ordered string took even longer--53.2 seconds--because two
operations were required at each step to build the output string.
The major contribution to the time for the concatenation approaches
was construction of descriptors for the result strings: ATK utilizes
about seventy words of descriptor for each string. Even if this number
were cut to a tenth, however, descriptor allocation would still be
a major factor, both because of the time to initialize them and the
time for paging inherent in scattered control blocks. An alternative
implementation of immutable strings never copies the characters; instead
each concatenation generates a descriptor which points at the two halves
of the value. Thus string values are trees. It is unlikely that this
approach would improve performance since it does nothing to reduce
the number of descriptors nor the scattering of a string over a number
of pages. Indeed, for the case of concatenating one character at a
time the space allocated to descriptors will far exceed the space of
the strings themselves.
In summary, the performance degradation for completely immutable string
values was a factor of more than four.
7. Example: UnScribe
Scribe is a text formatting system which translates a document from
a coded form into instructions for a printer, and ultimately a printed
page. To illustrate the subsequence algebra we will write a translator
for a tiny subset of Scribe. In this subset two translations are defined:
Style-coded text is converted to styled text. For our purposes
a style-coded piece of text is written within braces preceded by an
at-sign and the name of a style; quoted text would be written as @quotation{text}.
The text may not contain a right brace.
Newlines are converted to spaces. Typically Scribe input is
editted with editors that deal best with short lines which Scribe translators
convert by changing newlines to spaces to merge the short lines into
paragraphs. The subset will have three rules which are applied in
this order:
-
-
1. If the newline is followed by a space, tab, newline, or other whitespace
character, the newline is left in the text.
2. Otherwise if the newline is preceded by a "sentence-ender" (period,
question mark, exclamation, colon, or semi-colon), it is replaced with
two spaces.
3. Otherwise the newline is replaced with a single space.
It is important to perform the two translations in the above order
because removal of the style codes may expose a sentence-ender just
before a newline. However, we will write the examples as two separate
functions each illustrating a different strategy for producing its
result.
ConvertStyles in Algorithm 1 translates the style codes of the text.
Since addStyles()
inherently modifies its argument, all of ConvertStyles will be done
by modification of its argument; thus it has no return value. The
heart of ConvertStyles is to locate a style name in a table and then
apply the corresponding style to the affected text. We can declare
the table as:
-
-- StyleTable gives the names of the various styles implemented,
-- each preceded and followed by a tab. Each name is
-- rendered in the typographic style that it denotes.
--
subseq StyleTable :=
" italic bold bigger"
~ " typewriter underline smaller"
~ " subscript superscript majorheading"
~ " heading subheading display"
~ " example description quotation"
~ " "
Each style name in this string is in the style denoted by the name;
"italic" is in italic, "underline" in the underline style, and so on.
Then when the name has been located in the table its first character
can serve as the second operand to addStyles().
The while loop in ConvertStyles cycles through the argument text looking
at each at-sign in turn and finding its subsequent left and right braces.
Each search is delimited by the end of the base text, but the test
- extent(finish(t), rightbrace) /= ""
checks to be sure the right brace is still within the bounds of the
original argument t. If not, or if one of the braces is missing, the
function exits without doing anything further. After finding a style
code, the name portion is looked up in StyleTable and, if found, is
used to apply the style to the affected text. Finally, the at-sign,
the style name, and the braces are deleted by replacing them with the
empty string.
Observe how the subsequence algebra supports locating parts of the
text. After the variables atsign, leftbrace,
and rightbrace have been set pointing to the characters
they name there are simple expressions for the parts of the style expression.
The argument to addStyles is
- extent(leftbrace, rightbrace)
which selects the braces and the text between, all of which are given
the style. Then the deletion of the style name is just deletion of
- extent(atsign, leftbrace)
which deletes the at-sign, the left brace, and the style name between.
ConvertNewlines in Algorithm 2 illustrates the append-only style of
text modification. As pieces of the text are processed, they are copied
to the result value with ~:=. A subsidiary
variable, segstart, retains the location of the beginning
of the text that has not been copied to the result. Variable t
is changed so it always refers to the text that remains unprocessed
and eventually it becomes the empty string or a string without any
newlines. The while
loop exits when a search through the characters of t finds
no more newlines; at that time, the segment from segstart
to the end of t is copied to the end of the result value.
As each newline is located, the text is checked with span()
to see if any subsequent characters are white space. If so, t
is advanced beyond the white space and the newline is unchanged. However,
if there is no following white space the segment is copied to the result
and a space is appended instead of the newline. A search then tests
the character before the newline to see if it is a sentence-ender and,
if so, an additional space is appended to the result. Finally, a new
segment is initiated beginning just after the newline and t
is advanced to begin there as well.
In ConvertNewlines, observe how characters
and positions adjacent to the newline can be conveniently referenced
relative to the variable newline. The characters after
the newline begin at finish(newline)
and the character before the newline is previous(newline).
- function ConvertStyles(t)
subseq atsign, leftbrace, rightbrace, style
while True do
-- find the pieces of the next @style{...}
-- if any piece cannot be found, we are through
atsign := search(t, "@")
if atsign = "" then exit function end if
leftbrace := search(finish(atsign), "{")
if leftbrace = "" then exit function end if
rightbrace := search(finish(leftbrace), "}")
if rightbrace = ""
or extent(finish(t),
rightbrace) /= "" then
exit function
end if
-- the 'style' name is between finish(atsign)
-- and start(leftbrace)
-- the text to be styled is between
-- finish(leftbrace) and start(rightbrace)
-- find the style in the table
style := search(StyleTable,
"\t" ~ extent(finish(atsign),
start(leftbrace)) ~"\t")
if style /= "" then
-- okay, convert a style
-- add the style to the text and delete
-- the control text
-- the braces can be styled because
-- they are deleted anyway
-- the second character of 'style' is used
-- because the first is the tab
-- and may not have the style
addStyles(extent(leftbrace, rightbrace),
next(front(style)))
replace(extent(atsign, leftbrace), "")
replace(rightbrace, "")
end if
-- set t to continue looking for @ signs
t := extent(finish(rightbrace), t)
end while
end function
-
Algorithm 1. ConvertStyles. Style codes of the form @style-name{...text...}
are converted so the text has the named style and the control infromation
is deleted.
- function ConvertNewlines(t)
-
subseq result -- holder for final result string
subseq segstart -- portion scanned but not yet moved
-- to result is extent(segstart, start(t))
subseq newline, space -- temporaries within the loop
result := newbase() -- initially there is no result
segstart := start(t) -- initially the segment is empty
while True do
-
-- find the next newline character
newline := search(t, "\n")
if newline = "" then exit while end if
-- find the whitespace characters after newline
space := span(extent(finish(newline), t),
characters_whitespace)
if space /= "" then
-
-- newline followed by white space,
-- leave it as is
t := extent(next(space), t)
else
-
-- newline to convert to space(s)
result ~:= extent(segstart,
start(newline)) ~ " "
if search(characters_sentenceEnder,
previous(newline) /= ""
then
-- sentence ends before newline:
-- use two spaces
result ~:= " "
end if
-- skip the newline
-- and continue with the rest of t
segstart := finish(newline)
t := extent(segstart, t)
end if
end while
result ~:= extent(segstart, t)
return result
end function
-
Algorithm 2. ConvertNewlines. The result value is constructed
with append-only modification of a result string.
8. Implementation
The four primitives of the subsequence algebra--start, base, next,
and extent--are not a symmetric set of operations; next()
moves from left-to-right and the corresponding right-to-left operations
are non-primitive. This asymmetry reflects a design decision to engineer
the primitives for the most common order of examining text. In some
implementations there may be a performance penalty for right-to-left
traversal, for instance it may be harder to go backwards over a multi-byte
character representation than forwards.
An implementation of the substring algebra must provide data structures
for both substring values and their underlying base strings. Additional
data structures are needed for typographic styles and embedded objects,
to whatever extent they are supported by the implementation. The Ness
implementation of the algebra relies on the Andrew ToolKit (ATK) implementations
of these data structures, so the language development entailed little
new data structure design.
In ATK, text is represented in memory as a physical sequence of characters.
To support text editting and other text manipulation, the space for
a base string is made larger than the string itself and the extra character
positions are retained as a gap within that base at the position of
the most recent replace(). If consecutive
replaces tend to happen at nearby locations, the overhead of copying
characters to make changes is minimized [Hansen, 1987].
One alternative to physically sequential storage of characters is to
store each character as an element in a list. With this approach it
is far faster to splice an element into the sequence. However, performance
degrades with increased paging as the list gets fragmented over an
increasingly large number of pages. Experience has demonstrated that
keeping the text sequential reduces paging sufficiently to offset the
costs of copying strings when changes are made. Of course there are
numerous intermediate data structure designs with linked lists of elements
each having a physically sequential block of text. We have not tried
this approach because the physically sequential approach has worked
sufficiently well.
It is important to keep the representation of substring values as small
as possible because they are so often created and destroyed. The minimal
implementation of an immutable substring is three words: a pointer
to the base, and representations of the start and end of the substring.
For mutable substrings a fourth word must be added to link this value
to other substrings on the same base.
When an expression mentions a subseq value, the compiler produces code
which copies that value (or a pointer to a copy of it) to the stack.
Then the various operations of the expression modify the copy without
modifying any variables. For instance, start()
is one instruction which changes to zero the representation of the
length of the substring reference. Finally, if the value of the expression
is assigned to a variable the value on the stack is copied into the
variable. For a simple assignment like
- a := start(b)
the stack is an inefficient mechanism. An optimizing compiler can
implement this by copying the subseq value b into a
and then modifying a to have zero length. If a
and b are immutable values and we are compiling for the
IBM RISC architecture, the assignment could take as few as three instructions:
a load-multiple and store multiple to transfer the subseq representation
and a store-immediate to set the length of the result value to zero.
When there are more operations in the expression, the overhead of
copying the initial value is distributed among them all and is thus
proportionately lower.
Implementations of start(), base(),
and extent()
all require simple pointer arithmetic. Next()
may be more complex because it is the one operator which must determine
how many bytes in the representation of the base sequence correspond
to the next object. If some characters or objects take more than one
byte, next()
must determine this to compute the appropriate reference.
In ATK, both styles and embedded objects are implemented with a tree
of nested environments associated with the base text. Each
node of the tree partitions the text controlled by its parent and each
node--internal or leaf--specifies a style for its partition. Thus
italic text can be contained within a partition which is in the indented
style. For embedded objects the environment is a leaf and refers to
a single dummy character in the text; additional information in the
environment indicates what actual object is included at that position.
The existence of these dummy bytes makes next()
faster.
As an optimzation, the implementation can be organized to provide an
actual array of integers or object pointers when the environments indicate
a consecutive succession of such items. With this implementation,
array operations can be reasonably close in efficiency to arrays in
other languages.
Storage management is essential when a language provides Unbounded
Strings and Concatenation. For most purposes reference counting of
string values is sufficient because circular structures cannot be created.
However, with obj()
a program may create circular structures so automatic storage reclamation
is necessary.
9. Summary and Open Questions
This paper has explored the question of what string operations are
suitable for a high level language designed to deal with multi-media
text. Many advantages have been demonstrated for an approach wherein
the only string values are references to portions of underlying base
strings. Such values can be manipulated conveniently with an algebra
whose primitive operations include start(), base(), next(), extent(),
replace(), and newbase(). With these operators a simple exercise,
printsubsequences, shows that all substrings can be computed. By demonstrating
appropriate functions, the paper showed how the algebra deals with
pattern matching, multi-media text, and modification of strings.
The string facility as described has the properties of Unbounded strings,
Multi-Media Text, Substring References, an Algebra for Substrings,
and Mutable substrings. Are all these necessary for an ideal string
capability? Not necessarily; here are some of the options for language
designs:
Unbounded strings - In these days of large memories and fast
storage allocators, it is difficult to justify a requirement that the
size of all strings be known when the program is written. If this
restriction is made, however, it is imperative that the implementation
check that accesses to the string do not exceed the bounds.
Multi-Media Text - The decision to support multi-media text
in a language need not affect the language design itself in detail;
the major impact is on the implementation. In particular, the token
scanner must accomodate multi-media text. The run-time package can
share tools for management of multi-media text with the program text
editor. Functions for access to typography and embedded objects must
also be provided; examples of such functions are sketched in Section
5.
Mutable Substrings - Even more than the other decisions, the
choice of mutable substrings is a matter of taste--some believe that
values should never change, others believe that immutability is a luxury
not yet supported by execution speed and memory capacity. One intermediate
option is append-only strings, where changes can only be made by appending
a new value to the end. If modification at other points in strings
is to be possible and Multi-Media is provided, it may as well be possible
to replace a substring with another of a different length; this follows
especially in those cases where the implementation uses a variety of
byte lengths for the representation of items in a string.
Substring References, Algebra for Substrings - The alternate
to providing these two features is to refer to locations within strings
by integers or pointers. The disadvantages of this approach are outlined
in Section 1; the advantages of Substring References are illustrated
by many of the examples above, especially the patterm matching operations
in Section 4 and the discussion of the examples in Section 7. When
arbitrary substrings are Mutable, an additional advantage of Substring
References is that they can be updated to continue to refer to the
same location; with integers or pointers the system would be unable
to update reference values when the string changed. If strings are
immutable or append-only, then the overhead of substring reference
values is minimal, as sketched in Section 8.
Substring reference values and the subsequence algebra raise many interesting
issues, including these:
1. What are patterns? Since pattern matching is a computationally
intensive operation, it is valuable to be able to precompile pattern
operations into efficient code, but what form of pattern description
is most conducive to compilation while at the same time convenient
to program. In SNOBOL4, patterns are values in their own right, which
requires definition of an entirely separate algebra of patterns in
addition to that of strings. In Icon, patterns are not types but are
implemented as functions which manipulate a semi-hidden scan variable
through the subject string. These provide for efficient compilation,
but it is not always clear how to transform a desired pattern into
the appropriate sequence of function calls.
With the string algebra it may be possible to define patterns as pure
functions. The argument would be a substring and the returned result
another, with some special convention to indicate a match failure.
Within a host language like Scheme which provides continuations, pattern
functions could return generator functions which would iterate through
all instances of a pattern in a subject string.
2. What is the best implementation data structure for base strings
and subseqs? While there may not be an answer satisfactory for all
applications, it is likely we can do better than our existing implementations.
The ATK structures for styles and embedded objects are rather heavy-weight;
would a simpler design have benefits even if more computation were
required in some cases?
3. What optimizations are most appropriate for compilation of subseq
expressions? For instance, code generated for next(start(base(x)))
would not necessarily have to go through each step to compute the first
character of the base. In an optimizing compiler, symbolic execution
of subseq expressions would enable generation of efficient machine
language code.
4. Are sequences useful for tasks beyond operations on strings? When
subseq values themselves are stored as elements in sequences they form
general list structures at least as expressive as Lisp S-expressions.
Does the string algebra lend itself to the same non-numeric applications
as Lisp? and would it offer reduced paging by preventing the scatter
of structures over numerous pages? or is the low overhead of CAR and
CDR a sufficient recompense for their limited capabilites? And how
will users react; will non-professional programmers find sequences
a more natural metaphor than linked lists for a wide range of computer
problems?
Acknowledgements. Bruce Sherwood was a bountiful source of
enthusiasm and encouragement; I am indebted to him, Judy Sherwood,
David Anderson and others at the Center for Design of Educational Computing,
Carnegie-Mellon University, who implemented and utilized the algebra
as part of cT. This work began with the support of the Science and
Engineering Research Council (Britain, grant number GR/D89028) and
the Department of Computer Science at the University of Glasgow, under
the stimulating direction of Malcolm Atkinson. The work benefitted
from conversations with Kieran Clenaghan, David Harper, Joe Morris,
and John Launchberry. Support for the Ness implementation in ATK was
provided by the IBM Corporation and the Information Technology Center,
Carnegie Mellon University under then director Alfred Z. Spector.
Helpful comments were offered by many at CMU, including Mike Horowitz,
Mike McInerny, Jim Lui, George Baggot, Tom Neuendorffer, and Judy Jackson.
References
[CDEC, 1989] Center for Design of Educational Computing, CMU, The
cTtm Programming Languge, Falcon Software (Wentworth,
NH, 1989).
[Hansen, 1987] Hansen, W. J., Data Structures in a Bit-Mapped Text-Editor,
Byte (January, 1987), 183-190.
[Hansen, 1989a] Wilfred J. Hansen, "The Computational Power of an Algebra
for Subsequences", CMU-ITC-083, Information Technology Center, Carnegie-Mellon
Univ., 1989.
[Hansen, 1989b] Wilfred J. Hansen, "Ness Language Reference Manual",
available on X-windows distribution tape as .../contrib/andrew/atk/ness/doc/nessman.d,
Information Technology Center, Carnegie-Mellon Univ., 1989.
[Hansen, 1990] Hansen, Wilfred J., "Enhancing documents with embedded
programs: How Ness extends insets in the Andrew ToolKit," Proceedings
of IEEE Computer Society 1990 International Conference on Computer
Languages, March 12-15, 1990, New Orleans, IEEE Computer Society
(New York, 1990), to appear.
[Morris, 1986] Morris, J., M. Satyarayanan, M. H.Conner, J. H. Howard,
D. S. H. Rosenthal, and F. D. Smith. "Andrew: A distributed Personal
Computing Environment," Comm. ACM, V. 29, 3 (March, 1986), 184-201.
[Morris, 1985] Morris, R. A., "Is What You See Enough to Get?: a Description
of the Interleaf Publishing System", PROTEXT II, Proceedings of the
Second International Conference on Text Processing Systems, (October,
1985), 56-81.
[ISO, 1988] ISO, Information processing--Text and Office Systems--Office
Document Architecture (ODA), ISO-8613, International Standards
Org., (1988).
[Palay, 1988] Palay, A. J., W. J. Hansen, M. Sherman, M. Wadlow, T.
Neuendorffer, Z. Stern, M. Bader and T. Peters, "The Andrew Toolkit
- An Overview", Proceedings of the USENIX Winter Conference,
Dallas, (February, 1988), 9-21.
[Sherman, 1990] Sherman, M., J. Rosenberg, A. Marks and J. Akkerhuis,
Multi-media Document Interchange: ODA and the EXPRES Project,
Springer-Verlag (Berlin, 1990).
[Spafford, 1989] Spafford, E. H., "Crisis and Aftermath," Comm. ACM
32, 6 (June, 1989), 678-687.
[Thomas, 1985] Thomas, R. H., H. Forsdick, T. Crowley, R. Schaaf,
R. Tomlinson, V. Travers, "Diamond: A Multimedia Message System Built
on a Distributed Architecture", IEEE Computer 18, 12 (Dec, 1985),
65-78.
References for programming languages
[Adobe, 1985] Adobe Systems, Inc., Postscript Language: Reference
Manual, Addison-Wesley, (Reading, Mass., 1985).
[ANSI, 1978] ANSI, American National Standard - Programming Language
- FORTRAN, ANSI X3.9-1978, ANSI (NY, 1978).
[ANSI, 1985] ANSI, American National Standard for Information Systems
- Programming Language - COBOL, ANSI X3.23-1985, ANSI (NY, 1985).
[Atkinson, 1987] Atkinson, B., HyperCard, Version 1.0.1, M0556
/ 690-5181-A, Apple Computer (Cupertino, CA, 1987).
[Cardelli, 1988] Cardelli, Luca, J. Donahue, L. Glassman, M. Jordan,
B. Kalsow, G. Nelson, Modula-3 Report, Research Report 31, Digital
Systems Research Center, (Palo Alto, CA, 1988).
[DOD, 1980] U. S. Department of Defense, Reference Manual for the
Ada Programming Language, Draft Revised MIL-STD 1815, Order Number
1008-000-00354-8, U. S. Government Printing Office (Washington, 1982).
[Griswold, 1971] Griswold, R. E., J. F. Poage, and I. P. Polonsky,
The SNOBOL4 Programming Language, Prentice-Hall (Englewood Cliffs,
1971).
[Griswold, 1983] Griswold, R. E. and M. T. Griswold, The Icon Programming
Language, Prentice-Hall (Englewood Cliffs, 1983).
[IBM, 1987] IBM Coporation, Common Programming Interface Procedures
Language Reference, SC26-4358-0, IBM (Endicott, NY, 1987).
[Kernighan, 1978] Kernighan, B. W. and D. M. Ritchie, The C Programming
Language, Prentice-Hall (Englewood Cliffs, 1978).
[Microsoft, 1981] Microsoft Corp., Basic, 6025013, IBM Corp.
(Boca Raton, FL, 1981).
[Steele, 1984] Steele, G. L., Jr., Common Lisp: The Language,
Digital Press (Bedford, MA, 1984).
[van Wijngaarden, 1976] van Wijngaarden, A. et al., Revised Report
on the Algorithmic Language Algol 68, Springer-Verlag (New York,
1976).
[Wirth, 1974] Wirth, N. and Kathleen Jensen, Pascal User Manual
and Report, Lecture Notes in Computer Science, 18 Springer-Verlag,
(Berlin, 1974).
Appendix A. String Modification Benchmark
This benchmark compared various methods of creating a new string value.
Each of the alternatives produced a new copy of the string s by iterating
through it character by character and putting each in turn into the
new value. For each test the bold face line in the loop body was replaced
with one of the pieces of code listed below.
- function main()
subseq p, t, mid, s
s := " <a string of 5120 digits> "
p := newbase()
t := first(s)
while t /= "" do
-- Replace this line for each test.
t := next(t)
end while
end function
Here are the various tests. They were executed on an IBM RT/APC with
8 megabytes of memory. The times in parentheses give the average time
for this test; before subtracting the time for the iteration alone.
The time does not include the time to create s. Each test
was run ten times to generate the averages shown; variance in the results
was low with few repetitions differing from the average by more than
half a second.
{Nextn(s,n)
applies next()
a total of n times to its argument s. In practice
this is quite fast because it is implemented with address arithmetic
instead of scanning s.}
Determine the time for the iteration alone (4.5 seconds):
- p := p
Build the destination value by appending to it (8.9 seconds):
- p ~:= t
Reverse the string using replace() to insert each character at the
front (9.1 seconds). (Since append is virtually identical to replace()
at the end of the string, a reversed output was created.)
- p := base(replace(start(p), t))
Build the destination by concatenating each character to the existing
destination (34.1 seconds):
- p := p ~ t
Determine the iteration-only time for placement at a random location
(13.6 seconds):
- mid := start(nextn(start(p),
random(length(allprevious(t)))))
p := base(mid)
Produce a disordered copy by insertion at a random location (25.2 seconds):
- mid := start(nextn(start(p),
random(length(allprevious(t)))))
p := base(replace(mid, t))
Produce a disordered copy by concatenating at a random location (66.8
seconds). (The compiler/interpreter converts the two concatenations
into a concatenation and an append.)
- mid := start(nextn(start(p),
random(length(allprevious(t)))))
p := extent(p, mid) ~ t ~ extent(mid, p)
obsolete references
[Alpert & Bitzer, 1970] Alpert, D., & D. L. Bitzer, Science 167,
1582 (1970).
[Gimpel, 1976] Gimpel, J. F., Algorithms in SNOBOL4, John
Wiley & Sons (New York, 1976).
[Griswold, 1980] Griswold, R. E., and D. R. Hanson, "An Alternative
to the Use of Patterns in String Processing," ACM TOPLAS, 2,
2 (April, 1980) 153-172.
[Hansen, 1987a] Hansen, W. J., Ness - Reference Manual, Computer
Science Dept., Univ. of Glasgow, 1987.
[Hansen, 1987b] Hansen, W. J., Em - Reference Manual, Computer
Science Dept., Univ. of Glasgow, 1987.
[Sherwood, 1977] Sherwood, B. A. The TUTOR Language, Control
Data Education Co. (Minneapolis, 1977).
[Sherwood, 1986a] Sherwood, B. A., and J, N, Sherwood, The CMU-Tutor
Language, Preliminary Edition, Stipes Publishing Company (10 Chester
Street, Champaign, Ill., 1986).
[Sherwood, 1986b] Sherwood, J. N. CMU Tutor Reference Manual.
Center for Design of Educational Computing, Carnegie-Mellon University
(Pittsburgh, 1986). (This is a printed version of the on-line reference
manual.)
Notes for Enhancements
Define and describe various models of string values:
FORTRAN, COBOL, Pascal: Static allocation
C, Algol-68, Ada: static and dynamic allocation.
SNOBOL, Icon, Basic: system allocates
Describe why full mutability makes implementation as a subroutine package
difficult. In particular, evaluate each of the 14 languages and say
which can support the algebra directly as functions. Note that the
language must be able to redefine assignment for the data type.
Note that a base continues to exist until there are no references to
subsequences of it.
Discuss array access to subseq elements.
Cover possible notations.
Concatenation: Algol68: +, Fortran: //, others: ||
Maybe: - for extent, + for next, @ for start, * for base
Show that the algebra extends to generators for infinite sequences.
base() returns a generator value
next(), extent(), and start() are all well defined
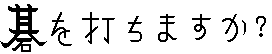 is Japanese for Do you play go?"
is Japanese for Do you play go?"