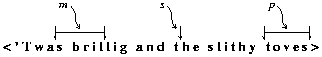

Copyright ACM, 1992. Published in ACM Trans. Programming Languages and Systems, 14 (4), Oct., 1992, pp. 471-489.
This paper informally presents the data type, demonstrates its convenience for defining search functions, and shows how it can be concisely implemented. Examples are given in Ness, a language incorporating the new data type which is implemented as part of the Andrew Toolkit.
Keywords: strings, substrings, sequences, subsequences, programming language design, string searching, document processing, Andrew Toolkit, ATK, Ness
Text and string operations are increasingly important as word processing becomes one of the most common computer applications, especially for non-technical people. Despite the importance of strings, programming languages have offered no innovations in string data types or operations since the introduction of pattern matching and substr which happened at least as early as COMIT [Yngve, 1963] and PL/I [IBM, 1965], respectively. The most recent innovations are in control structures; in particular, Icon [Griswold, 1990] has introduced goal-directed evaluation. This integrates string scanning with the rest of the language, whereas pattern matching is a sub-facility in earlier languages like COMIT and SNOBOL4 [Griswold, 1971].
In some languages strings and string expressions are first-class values in that they are eligible to appear in all contexts that permit any other expression, including assignment, function parameter, and return value. Substrings, however, do not have first class status. To represent one usually requires multiple assignments and multiple variables with the concomitant increase in complexity and potential for errors. Records, structs, or other composite values can sometimes be utilized, but this still requires the programmer to be aware of the details.
First-class values are especially important in the applicative programming style, which eschews side effects and thus has little room for values of other classes. Although applicative programming has sprung from a desire to prove properties of programs, it can also play a role in making it possible for more people to program. [Hughes, 1989]
This paper defines and demonstrates subsequence references, a first-class data type for subsequences in general and substrings in particular. In this data type, each value is a reference to a subsequence of a base sequence, so each single value represents an entire subsequence. The presentation in this paper is informal; for a formal definition of the data type, see [Hansen, 1989a].
Subsequence references are but one of several models of string values:
Atomic. In the atomic model of strings each string value is a distinct object with no accessible constituents. Operations and string functions return values that are effectively new strings with no relation to other existing strings. Given the right implementation, atomic strings can certainly be first-class, however, they are not always simple to use. Problems arise for parsing and searching operations because the result of a search must report not only the string which matched, but also its position. For instance, a calling routine may need to test punctuation adjacent to a returned value.
Although there are no major languages with a pure atomic model of strings, the possibility has been demonstrated by Eli [Glickstein, 1990]. In this Lisp-like language, search functions return a list of three strings whose concatenation will recreate a value equivalent to the original subject string. The middle element of the list satisfies the search specification.
Starting no later than XPL [McKeeman, 1970], implementations of functions for atomic string values have not actually copied strings to produce new values. Instead each return value is a reference to a substring of one of the argument strings, which thus serves as a base for the value. This technique is also employed for the implementation described below, with the difference that the new data type offers functions for accessing elements of the base string outside the referenced substring.
Indexed. In the indexed model a string value is a pointer to a string or an integer index to an element of a string (usually the latter is an atomic string). Such values can easily be first-class since integers and pointers are themselves first-class, but substrings are not first class because two values are required to refer to an arbitrary substring. When a programmer takes a shortcut to utilize one variable as a basis for locating two or more substrings, there is a potential for off-by one errors. Programmer effort is also increased when forced to choose between the atomic and indexed models. The formal complexity of the language is increased by having recourse to a domain--integers or pointers--outside the domain of strings.
C is one well-known example of a language with indices implemented
as pointers; a string value is a pointer to a string or a tail of
a string. To refer to a subsequence in C a composite value is required.
For instance a token scanner might utilize the type StringPiece:
Integer indices to strings are found in many languages, including PL/I and Fortran. These are not entirely equivalent to pointers when a string is copied: integer indices into the original will refer to the same positions in both copy and original, while pointers will refer only to a position in one string or the other.
Icon.
Icon provides a special operator, ?, for pattern scanning. The expression
Icon functions can generate a sequence of values, for example, many(letters) generates the positions of each run of letters in the subject. Icon's goal-directed evaluation mechanism initiates backtracking in appropriate contexts, which consumes successive values until one satisfies the search. For instance, s ? { tab(many(letters)) & ="()" } determines if s contains a run of letters followed by (); backtracking tries each value of many(letters) in turn until one is found followed by () or no more can be found.
Not only does Icon have the complexity of offering both the atomic and indexed models of string values, but there are separate sets of functions for each. There is a potential for confusion between tab and move, which return atomic string values, and many, upto, and the other functions which return indices. Indeed, it would be interesting to know if omission of required tab and move operations is a common error in Icon programs.
Subsequence references. Each subsequence reference value incorporates both a subsequence value and the position of that value within its base. When given first-class status by a programming language, such are ideal to return from parsing or other searching/scanning operations. As discussion of the various Algorithms below will show, it is common to utilize a single variable both for its value and its position. In all cases, other string models would require additional variables and assignment statements.
Although internally more complex than integers, subsequence references simplify programming by reducing the required number of concepts. Atomic values and indices are subsumed by the single model and there is no need for recourse to a domain outside of subsequences. Moreover, subsequences largely eliminate the need for separate data types for character and string values, both of which can be represented as references to appropriate subsequences.
Subsequences can be viewed as a generalization of Icon's &pos and &subject; however subsequences can appear in any context, not just within string scanning. Moreover, subsequence references can be used in iterations requiring scanning two strings in parallel. For example, an interpreter for a pattern matching language would need to advance simultaneously across one sequence representing the subject and another representing the pattern.
The subsequence reference data type has been implemented in two languages:
Ness [Hansen, 1989b; Hansen, 1990] and cT [CDEC, 1989]. Both were
originally implemented under the Andrew Toolkit (ATK) [Morris, 1986;
Palay, 1988], although cT has recently been re-implemented. The capability
range of ATK is illustrated by this paper: a single file with various
embedded objects created using ATK's ez text editor. Examples below
are given in Ness, the implementation of which permits typographic
styling and embedded objects in program text and constants; the program
fragments below were compiled and executed with the styles as shown.
A sequence is a finite, ordered collection of elements from the arbitrary set. Before each element and after the last is a "position".
A subsequence reference or subseq is a triple [b,
l, r] where b is a sequence and l and r
are positions in b.
Figure 1 shows three subseq values, m, s, and p, defined on the base sequence "'Twas brillig and the slithy toves" and referring respectively to "s bril", an empty subsequence, and "toves".
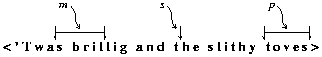
The most basic operators defined for subseq values are start, base, next, and extent as illustrated in Figure 2 and defined thusly:
base(x) - Returns a subseq for the entire base of x. Specifically,
the return value is on the same base as x and has the two
positions at opposite ends of that base.
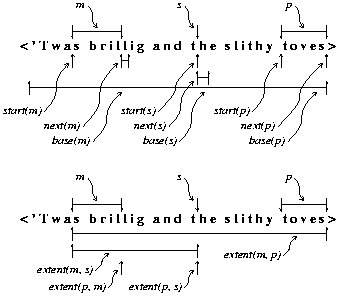
In the Figure, start(m) is the empty subseq between a and s; and the values of base(m), base(p), and base(s) are each the entire sequence between < and >. To get an empty subseq at the beginning of x's base sequence, we can write start(base(x)). The opposite composition, base(start(x)), returns exactly the same value as base(x) because x and start(x) share the same base.
Next(m) and next(s) in the figure are both single elements, while next(p) is empty. The element just after the beginning of x is next(start(x)), while the empty subseq at the end of x is start(next(x)). Next(base(x)) is the empty subseq at the end of base(x).
One non-empty result in Figure 2 is extent(s, p) which extends from s to the end of the base; conversely, extent(s, m) gives an empty subseq at the same position as extent(p,m). All of the base before m is extent(base(m), start(m)) and all of the base after m is extent(next(m), base(m)); observe that the result for both is shorter than base(m) even though it is one of the arguments.
To create new base values it suffices in this paper to provide constants and concatenation:
x ~ y - Tilde denotes concatenation and generates a new base string composed of copies of the subsequences referred to by x and y. The value returned is a reference to the new base string with positions at its opposite ends.
In terms of Figure 2, m ~
p
is a subseq whose base is the new value "s briltoves" and whose
positions are at the extremes of that base.
In examples below, subseq variables are declared with the form:
Given a subseq value we can write simple loops to scan through a base
string. If m refers to a blank, we can advance it to point
to the nearest following non-blank with:
Suppose m refers to a word, that is, consecutive non-blank characters with adjacent blanks on both ends. To find the next word we must first skip the blanks following m and then build a subseq referring to everything prior to the next blank. In Ness this is written as:
The first while loop scans across all blanks after m and the second scans across all subsequent non-blanks to accumulate the word. The test next(m) /= "" checks to see if m ends at the end of its base, in which case it is deemed to be at the end of a word. When there is no word, nextword returns an empty string.
Even this brief example can illustrate the first-class nature of subseq
values; that is, that a subseq value returned by one function can
be directly passed as an argument to another. For instance the statement
The operators start and next are asymmetric with
respect to text order in that one moves from left-to-right and the
other returns the leftmost position in its argument, while the corresponding
operators for the reverse direction are non-primitive. This asymmetry
reflects a decision to engineer the primitives for the most common
order of examining text. Indeed, some implementations utilizing multiple
encoding widths for characters may impose a performance penalty for
right-to-left traversal.
Finish is analogous to start and also produces
an empty subseq, but at the other end of its argument. Functions front,
first, last, and previous all produce
subseqs for single elements analogously with next. Rest(x)
returns a subseq one element shorter than x.
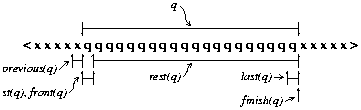
| Function | Definition | Expression |
| finish(x)
| the empty string at the position where x ends
| start(next(x)) |
| front(x)
| the element which starts where x starts (even if x is empty) | next(start(x)) |
| rest(x) | all of x past its first element (empty if x is empty) | extent(next(front(x)), x) |
| first(x) | first element of x, but empty if x is empty
| extent(x, start(rest(x))) |
| last(x) | the last element in x, or x itself, if empty | {see text} |
| previous(x) | the element preceding x | last(extent(base(x), start(x))) |
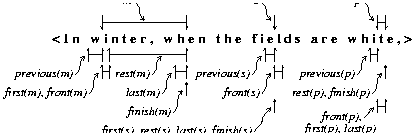
Figure 4 illustrates further the non-primitive functions of Table 1. Here variable m has the same properties as q in Figure 3 and variables s and p show the results for empty and one element values, respectively. First and front differ in their values only for the empty subseq s; in this case, first(s) is s itself and front(s) is the element next(s).
The expressions for rest and first exploit the definition of extent. When x has one or more elements, the value of next(front(x)) begins just after the first element, so the expression for rest produces a value extending from just after that first element to the end of x. When x is empty, its end precedes the start of next(front(x)), so the result for rest is the empty subsequence at the end of x, which is the same value as x itself, as per the definition of rest. The same trick applies in the definition of first, which gives the single element preceding rest(x) if x is non-empty, but otherwise x itself.
With the aid of rest we can write an elegant, recursive definition
of last:
The search operations below each have two arguments, a subject and a specification. By convention, the subject argument determines the range to be searched according to this rule: If the subject argument is non-empty, the range is the subject; but if the subject is empty, the range extends from the subject to the end of its base. Since a successful search always yields a non-empty subsequence, failure is indicated by returning an empty subseq value, usually the one at the end of the subject argument. By these conventions, if the range is to extend from the position given by empty subseq p to the end of its base, the calling function can choose that the failure value be either p or finish(base(p)) by passing as the subject either p or extent(p, base(p)), respectively.
In the descriptions below, when the second argument--the specification--is
obj, the match must be an exact match, element-for-element;
but when it is set, the string is treated as a set. A typical
set value is "0123456789" for the set of all digits. These functions
are illustrated in Figure 5.

With the search operations we can now rewrite nextword of Section 1 more briefly as
To define the search functions in terms of the primitive operations, we begin with a support function which searches a string src looking for an instance of a character c. If found, a subseq for the instance is returned, otherwise the value returned is an empty subseq at the end of src:
This function illustrates one form of loop; at each cycle around the while loop, src is one character shorter by virtue of the call on rest(src). The loop ends if either src becomes empty or its first character matches c. The loop invariant is that c is not equal to any character in extent(src0, start(src)), where src0 denotes the initial value of src.
Algorithm 1 expresses span in terms of findchar and the primitive operations. The first if-then sets s to be the range of the search as defined by the search conventions. The loop, as above, calls rest(s) at each step to shorten s by one element. As one example of multiple usage of a subsequence reference, note that variable s is utilized for its first character with first(s), its position with start(s), and its extent with rest(s).
Sometimes a loop advances through a string in steps longer than one character at a time, as illustrated by the search function in Algorithm 2. Each cycle of the while loop calls findchar to find the first character of obj and then calls match to determine if all of obj has been found. If so the appropriate value is returned, but if not, there is no point to re-checking extent(s, f), so s is set to everything after f. If s becomes empty, findchar returns an empty subseq and the loop exits via the test of f = "".
Algorithm 2 again illustrates multiple usage of subsequence reference values; the contents of f are tested and the positions of both ends appear in expressions. Since both f and m are on the same base as s, the new value of s can be set to begin after f and the value of m can be returned, each retaining its position in the original base string.
In the Ness implementation, search is implemented with a far faster
non-linear search [Sunday, 1990]. The details of match,
token, and trim
are left as exercises to the reader.
A line must be normalized if it has the form:
<WS> # <WS> <key> <WS> <text> <WS> <newline>
where <WS> is optional whitespace, <key> is one of five words, and
<text> is arbitrary text. When <key> is if, ifdef, or
ifndef the output is
# <key> <space> <text> <newline>
but when <key> is else or endif the output for empty <text>
is
# <key> <newline>
and for non-empty <text> is
# <key> <space> /* <space> <text> <space> */ <newline>
Note that the latter case must strip existing comment delimiters from
<text>. If the input line does not have one of the expected forms, it
is returned unchanged.
The essence of NormalizeLine is to first locate <key>
and <text> in the input line and then--if the line is in one of
the above forms--build the output from those values. For building
the output, the algorithm relies on a table giving the output for each
of the five key values. Since Ness has neither arrays nor structures
such tables are commonly represented in programs as strings where the
key is specially delimited so it can be found with a search. Then
associated data is taken from subsequent fields. For NormalizeLine,
a suitable table is
Algorithm 3 utilizes keytable to accomplish the task of building the output. The omitted portions of NormalizeLine determine that the line is a preprocessor statement, set k to the keyword, and set t to the text after the keyword. The call on search then locates k in keytable. The last three statements utilize the fields following the key in keytable to build the appropriate return value.
The usage of function nextfield in Algorithm 3 must be emphasized. Since its return value is an entire field, that value is suitable for concatenation to construct the result as in the final return statement. But since its value is a subsequence reference, it can also serve as argument to a function (in this case, itself) to locate and return the next following field, as in nextfield(nextfield(fix)). In other languages, a composite value would be required as with typedef StringPiece in the introduction, and even then the body of nextfield would have a number of additional assignment statements.
The full NormalizeLine function appears in Algorithm 4. The scanning portion of the algorithm tracks with variable t the current position of the scan within the line. Skipwhite advances past spaces and tabs; it could easily be written in a language with the index model of strings since it effectively returns a position. The algorithm begins by skipping whitespace, checking for a "#", and skipping more whitespace. Next, k is set to <key> by spanning subsequent letters and <key> is sought in keytable with the result being assigned to fix. The trim expression gives t a value extending from the first non-whitespace character after <key> to the last non-whitespace character on the line. The remainder follows Algorithm 3, with the addition of code to remove redundant comment delimiters.
As experiments the author and one of the referees wrote versions of NormalizeLine in C and Icon. The code is considerably longer in C because more variables are required to keep track of both ends of segments of the input line and because of the C tradition of in-line loops for string scanning. The C code also has an egregious bug in that it returns memory allocated in three different ways. For an unchanged line the original input is returned; for a #else or #endif with no comment, a constant is returned; and otherwise newly allocated memory is returned. Since the calling routine cannot easily distinguish these cases, it will probably not deallocate the allocated memory, leading to a core leak proportional to the number of preprocessor statements.
The Icon version was very elegant because it could take advantage of
the ? string scanning operator, backtracking, failure, and Icon's table
and record features. By its nature, however, the problem did not exploit
Icon's goal-directed execution mechanism. In general, the string scanning
operations were scattered in the program among the operands to other
functions. Assignments could have reduced this convolution, at some
expense in elegance.
The biggest problem is management of string storage: to conserve space,
a base sequence can and should be deleted when no subseq refers to
it. In a low-level language like C which does not provide storage
management, the string manager must keep track of all subseqs to manage
their space and that of the base sequences. However, this may not
be possible. Consider expressions where a string value returned from
one function is passed as argument to another, as in this fragment
from Algorithm 4:
When successfully implemented as a package, subsequence references must be defined in terms of some more primitive notion of strings provided in the language itself. This means two separate string mechanisms with an attendant loss in efficiency and increase in the number of concepts a program reader may encounter.
Finally, a string facility requires lexical support for string constants
and a primitive operation--preferably syntactic--for concatenation.
Given the deficiencies of a library implementation, it is reasonable to assume that we are implementing subsequence references as the native tool for strings in a high level programming language. Although this paper has not claimed interest in efficiency, it turns out that subsequence references can be implemented without undue overhead. Should the data type become widely used, appropriate compiler optimizations or tailored hardware will ensure acceptable execution speed.
Central to an implementation are data structure definitions for subseq values and base strings. Additional data structures are needed for typographic styles and embedded objects if they are to be supported by the implementation. The Ness implementation relies on the Andrew ToolKit (ATK) data structures, so little new data structure design was necessary.
In ATK, base strings are stored as a physical sequence of characters in a space larger than the string itself. The unused space is retained as a gap within the base at the position of the most recent modification (since ATK and Ness allow modification of base sequences) [Hansen, 1987]. If consecutive modifications tend to happen at nearby locations, the overhead of copying characters to make changes is imperceptible.
One alternative to physically sequential storage is a list of characters. Insertions and deletions are far faster, but space requirements mushroom and performance degrades with increased paging as the list gets fragmented among many pages. Experience has demonstrated that sequential text storage reduces paging sufficiently to offset the cost of copying strings when changes are made. Of course there are numerous intermediate data structure designs with linked lists of elements each having a physically sequential block of text. We have not tried this approach because the physically sequential approach has been satisfactory.
Section 1 noted that the implementation of subsequence references is
similar to many string packages, dating back at least as early as [McKeeman,
1970]. In that work only a position and length were recorded for each
string, whereas the minimal implementation of an immutable subseq is
three words: a pointer to the base, and representations of the leftmost
and rightmost positions. When the elements are stored consecutively,
integers suffice to indicate positions, so a subseq value can be described
in C as:
Operations on subsequence references are most succinctly implemented by modifying their argument, so, in an applicative environment, the code compiled to pass a subseq as an argument copies its value. Suppose these values are struct subseqs as above with x as the first argument and y the second. Then the four primitive functions can be compiled as if they were:
For a simple assignment like
Invariants. In writing invariants, it is often desirable to express attributes of subsequences. As shown in various of the examples above, invariants can be succinctly expressed with subsequence expressions.
Integer indices. While subsequence references permit ignorance
of the indexed model of strings, it does not preclude it. For instance,
the primitives are sufficient to implement nextn(s,
n)
as a function which applies next a total of n
times starting with the initial value s. Then the traditional
function substr(s, i, j)--which returns
the substring of s starting with the i'th character
and extending for j characters--is expressible as
Arrays. With nextn and a simple trick, sequences can subsume one-dimensional arrays. The trick is to address the array by a reference to the empty element at its start. Thus if A is an array, nextn(A, i) returns the i'th element of the array. A more elaborate language could offer bracketed subscripts as syntactic sugar for array access.
Formatted text. Operations such as applying and testing typographic styles are conveniently defined with subsequence references because a style naturally applies to a subsequence of the text. In the Ness implementation, functions are provided to apply styles, remove them, interrogate the style of text, and traverse the text in sections delimited by style change boundaries.
Embedded Objects and Multi-media. The contents of sequences need not be restricted to characters. Because Ness is implemented under ATK it permits elements which are raster images, spreadsheets, and numerous other objects. As ATK is extended to provide objects for voice recordings, video clips, and other multi-media components, these too will be potential elements of Ness sequences.
Mutability. Much literature has been devoted to applicative versus imperative programming. The subsequence data type has been presented in a purely applicative form above, but a sequence modification operator can easily be defined (and not quite so easily implemented). Replace(s, r) modifies the base sequence of s so the portion that was referred to by s contains a copy of r. Insertions and deletions are special cases of replacement. In some applications--for instance, text editors--where the base may have numerous subseqs referring to its parts, such modification can be a useful tool because the other subseqs remain attached to the base whereas if a new base were constructed it would have no subseqs on it. Replace is also useful when it can be employed to avoid creating new strings; the overhead of copying strings is not too bad, but the overhead of allocating memory and paging-in non-adjacent strings can be large.
General sequences. Subsequence references can subsume Lisp lists if subseq values can be objects embedded in sequences. The car() function would be re-interpreted to extract an embedded subseq as itself.
Unbounded sequences. Potentially infinite sequences can be
defined with a function to generate successive elements. The subsequence
data type is entirely adequate to deal with such sequences because
only the next
operator need access further along in the sequence--it would call
the generator if necessary. The base
operator would return a general sequence including a reference to
the generator function.
Many syntactic, semantic, and implementation questions concerning subsequence
references are as yet unanswered. However, by yielding a first-class
type for subsequences, the subsequence reference data type holds promise
of reducing program complexity and thus making it possible for more
people to exploit computers.
Acknowledgments. Bruce Sherwood was a bountiful source of enthusiasm and encouragement; I am indebted to him, Judy Sherwood, David Andersen and others at the Center for Design of Educational Computing, Carnegie-Mellon University, who implemented and utilized subsequence references as part of cT. This work began with the support of the Science and Engineering Research Council (Britain, grant number GR/D89028) and the Department of Computer Science at the University of Glasgow, under the stimulating direction of Malcolm Atkinson. Support for the Ness implementation in ATK was provided by the IBM Corporation and the Information Technology Center, Carnegie Mellon University under then director Alfred Z. Spector. Referee C patiently made numerous helpful comments.
[CDEC, 1989] Center for Design of Educational Computing, CMU, The cTtm Programming Language, Falcon Software (Wentworth, NH, 1989).
[Glickstein, 1990] R. Glickstein, "Lisp Primitives in ELI, the Embedded Lisp Interpreter", available on X-windows distribution tape as .../contrib/andrew/overhead/eli/doc/procs.doc, Information Technology Center, Carnegie-Mellon Univ., 1990.
[Griswold, 1971] Griswold, R. E., J. F. Poage, and I. P. Polonsky, The SNOBOL4 Programming Language, Prentice-Hall (Englewood Cliffs, 1971).
[Griswold, 1990] Griswold, R. E. and M. T. Griswold, The Icon Programming Language, 2nd Edition, Prentice-Hall (Englewood Cliffs, 1990).
[Hansen, 1987] Hansen, W. J., Data Structures in a Bit-Mapped Text-Editor, Byte (January, 1987), 183-190.
[Hansen, 1989a] Wilfred J. Hansen, "The Computational Power of an Algebra for Subsequences", CMU-ITC-083, Information Technology Center, Carnegie-Mellon Univ., 1989.
[Hansen, 1989b] Wilfred J. Hansen, "Ness Language Reference Manual", available on X-windows distribution tape as .../contrib/andrew/atk/ness/doc/nessman.d, Information Technology Center, Carnegie-Mellon Univ., 1989.
[Hansen, 1990] Hansen, Wilfred J., "Enhancing documents with embedded programs: How Ness extends insets in the Andrew ToolKit," Proceedings of 1990 International Conference on Computer Languages, March 12-15, 1990, New Orleans, IEEE Computer Society Press (Los Alamitos, CA, 1990), 23-32.
[Hughes, 1989] Hughes, J., "Why Functional Programming Matters," Computer Journal 32, 2 (1989).
[IBM, 1965] IBM Corporation, PL/I Language Specifications, C28-6571-0, IBM Corp., Data Processing Division, (White Plains, NY, 1965).
[McKeeman, 1970] McKeeman, W. M., J. J. Horning, and D. B. Wortman, A Compiler Generator, Prentice-Hall, Inc. (Englewood Cliffs, 1970).
[Morris, 1986] Morris, J., M. Satyarayanan, M. H.Conner, J. H. Howard, D. S. H. Rosenthal, and F. D. Smith. "Andrew: A distributed Personal Computing Environment," Comm. ACM, V. 29, 3 (March, 1986), 184-201.
[Palay, 1988] Palay, A. J., W. J. Hansen, M. Sherman, M. Wadlow, T. Neuendorffer, Z. Stern, M. Bader. and T. Peters, "The Andrew Toolkit - An Overview", Proceedings of the USENIX Winter Conference, Dallas, (February, 1988), 9-21.
[Sunday, 1990] Sunday, D. M., "A Very Fast Substring Search Algorithm," Comm. ACM 33, 8 (Aug, 1990) 132-142.
[Yngve, 1963] Yngve, V. H., "COMIT," Comm. ACM 6, 10 (Mar, 1963) 83-84.