SVM decision boundary based discriminative subspace induction
Jiayong Zhang and Yanxi Liu
The Robotics Institute, Carnegie Mellon
University, 5000 Forbes Avenue, Pittsburgh, PA 15213, USA
Received 15
October 2003; revised 24 January 2005; accepted 24 January
2005. Available online 9 April 2005.
We study the problem of linear dimension reduction for classification, with a focus on sufficient dimension reduction, i.e., finding subspaces without loss of discrimination power. First, we formulate the concept of sufficient subspace for classification in parallel terms as for regression. Then we present a new method to estimate the smallest sufficient subspace based on an improvement of decision boundary analysis (DBA). The main idea is to combine DBA with support vector machines (SVM) to overcome the inherent difficulty of DBA in small sample size situations while keeping DBA's estimation simplicity. The compact representation of SVM boundary results in a significant gain in both speed and accuracy over previous DBA implementations. Alternatively, this technique can be viewed as a way to reduce the run-time complexity of SVM itself. Comparative experiments on one simulated and four real-world benchmark datasets highlight the superior performance of the proposed approach.
Keywords: Dimensionality reduction; Linear dimension
reduction; Sufficient dimension reduction; Intrinsic discriminative subspace
(IDS); Decision boundary analysis (DBA); Support vector machines (SVM);
Classification; Regression ![]()
Dimension reduction is widely accepted as an analysis and modeling tool to deal with high-dimensional spaces. There are several reasons to keep the dimension as low as possible. For instance, it is desirable to reduce the system complexity, to avoid the curse of dimensionality, and to enhance data understanding. In general, dimension reduction can be defined as the search for a low-dimensional linear or nonlinear subspace that preserves some intrinsic properties of the original high-dimensional data. However, different applications have different preferences of what properties should be preserved in the reduction process. At least we can identify three cases:
1. Visualization and exploration, where the challenge is to embed a set of high-dimensional observations into a low-dimensional Euclidian space that preserves as closely as possible their intrinsic global/local metric structure [1], [2] and [3].
2. Regression, in which the goal is to reduce the dimension of the predictor vector with the minimum loss in its capacity to infer about the conditional distribution of the response variable [4], [5] and [6].
3. Classification, where we seek reductions that minimize the lowest attainable classification error in the transformed space [7].
In this paper we study the problem of dimensionality reduction for classification, which is commonly referred to as feature extraction in pattern recognition literature [8] and [9]. Particularly, we restrict ourselves to linear dimension reduction, i.e., seeking linear mapping that minimizes the lowest attainable classification error, i.e. the Bayes error, in the reduced subspace. Linear mapping is mathematically tractable and computationally simple, with certain regularization ability that sometimes makes it outperform nonlinear models. In addition, it may be nonlinearly extended, for example, through global coordination of local linear models (e.g., Refs. [10] and [11]) or kernel mapping (e.g., Refs. [12] and [13]).
PCA, ICA and LDA are typical linear dimension reduction techniques used in the pattern recognition community, which simultaneously generate a set of nested subspaces of all possible dimensions. However, they are not directly related to classification accuracy since their optimality criteria are based on variance, independence and likelihood. Various other dimension reduction methods have also been proposed, which intend to better reflect the classification goal by iteratively optimizing some criteria that either approximate or bound the Bayes error in the reduced subspace [7], [14], [15], [16], [17] and [18]. Such methods exclusively assume a given output dimension, and usually have the problem of local minima. Even though one can find the optimal solution for a given dimension, several questions still remain. How much discriminative information is lost in the reduction process? Which dimension should we choose next to get a better reduction? What is the smallest possible subspace that loses nothing from the original space as far as classification accuracy is concerned? Is there any efficient way to estimate this critical subspace other than the brute force approach, i.e. enumerating every optimal subspace for every possible dimension? The motivation for the present work is to explore possible answers to these questions.
For recognition tasks, finding lower dimensional feature subspaces without loss of discriminative information is especially attractive. We call this process sufficient dimension reduction, borrowing terminology from regression graphics [6]. The knowledge of smallest sufficient subspace enables the classifier designer to have a deeper understanding of the problem at hand, and thus to carry out the classification in a more effective manner. However, among existing dimension reduction algorithms, few have formally incorporated the notion of sufficiency [19].
In the first part of this paper, we formulate the concept of sufficient subspace for classification in parallel terms as for regression [6]. Our initial attempt is to explore a potential parallelism between classification and regression on the common problem of sufficient dimension reduction. In the second part, we discuss how to estimate the smallest sufficient subspace, or more formally, the intrinsic discriminative subspace (IDS). Decision boundary analysis (DBA), originally proposed by Lee and Landgrebe in 1993 [19], is such a technique that is promised, in theory, to recover the true IDS. Unfortunately, conditions for their method to work appear to be quite restrictive [20]. The main weakness of DBA is its dependence on nonparametric functional estimation in the full-dimensional space, which is a hard problem due to the curse of dimensionality. Similar problems have been observed in average derivative estimation (ADE) [21] and [22], a dimension reduction technique for regression in analogy of DBA for classification.
However, recent discovery and elaboration of kernel methods for classification and regression seem to suggest that learning in very high dimensions is not necessarily a terrible mistake. Several successful algorithms (e.g., Refs. [23], [24] and [25]) have been demonstrated with direct dependence on the intrinsic generalization ability of kernel machines in high dimensional spaces. In the same spirit, we will show in this paper that the marriage of DBA and kernel methods may lead to a superior reduction algorithm that shares the appealing properties of both. More precisely, we propose to combine DBA with support vector machines (SVM), a powerful kernel-based learning algorithm that has been successfully applied to many applications. The resultant SVM–DBA algorithm is able to overcome the difficulty of DBA in small sample size situations, and at the same time keep the simplicity of DBA with respect to IDS estimation. Thanks to the compact representation of SVM, our algorithm also achieves a significant gain in both estimation accuracy and computational efficiency over previous DBA implementations. From another perspective, the proposed method can be seen as a natural way to reduce the run-time complexity of SVM itself.
There are two basic approaches to dimensionality reduction, supervised and unsupervised. In the context of classification, a supervised approach is generally believed to be more effective. However, there are strong evidences that this is not always true (e.g., PCA and ICA might outperform LDA in face identification [26] and [27]). In this paper, we focus on supervised methods. According to the choice of criterion function, we further divide supervised methods into likelihood-based and error-based categories.
LDA is a time-honored reduction tool, which maximizes the Fisher's criterion (i.e., ratio of between-class over within-class variances). LDA is proven to be equivalent to the maximum likelihood solution to a Gaussian model subject to the equal within-class covariance constraint and reduced rank constraint on class centroids [28]. This likelihood-based interpretation of Fisher's criterion has led to several recent proposals. As the name suggests, heteroscedastic discriminant analysis (HDA [29] and [30]) allows unequal within-class covariance. When a diagonal covariance model is assumed, a special case of HDA called maximum likelihood linear transform (MLLT [31]) can be used to make the diagonal constraint more valid as evidenced from the data. Mixture discriminant analysis (MDA [32]) and nonparametric discriminant analysis (NDA [33]) extend LDA to non-Gaussian distributions and thus show greater flexibility. Penalized discriminant analysis (PDA [34]) is designed for situations with highly correlated features, such as sampled time-series or gray-scale pixel values, where a spatial smoothness constraint is imposed on the LDA coefficients. Exclusively, likelihood-based methods are not directly related to the classification error. Though LDA can be formulated as a generalized eigenvalue problem, its extensions above often require iterative computation.
Most error-based methods assume that Bayes error is a good criterion for comparing different feature (sub)spaces. As the full calculation of Bayes error is quite difficult, various error bounds have consequently been used in practice. These bounds are functionals of the marginal class densities of the projections, and can be evaluated by replacing the densities with their parametric or non-parametric estimates. For example, Bhattacharyya distance and Kullback–Leibler divergence are computationally simple for Gaussian distributions [17], while Patrick–Fisher distance [14] and maximum mutual information (MMI) [35] might be used with non-parametric densities. Recently, an improved approximation of MMI is proposed [18] that combines Renyi's quadratic entropy and Gaussian kernel density estimator. Besides using suboptimal bounds, there are also attempts to directly estimate the error functional itself [7], [16], [19] and [36]. An interesting property of these Bayes error-related algorithms is that they are classifier independent. For feature selection, the so-called wrapper approach has been popular for a long time which incorporates the classifier as part of the evaluation process in the search of the best possible feature subset. For linear dimension reduction, however, the joint optimality of dimension reduction and classifier design seems to be largely ignored. Discriminative feature extraction (DFE [15]) is one of the few exceptions that explicitly examine such interactions, which in essence minimizes a smoothed version of the empirical error.
To conclude this section, we summarize the supervised linear dimension reduction methods reviewed so far in Table 1. In the bottom row, we have listed some approaches that are not covered by our taxonomy due to their heuristic nature, including Fractional-step LDA (F-LDA [37]) and Fukunaga's NDA [38]. The “effortless” random projection (RP) has recently been used in learning high-dimensional mixture models [39]. Theoretical results indicate that it preserves distances quite nicely, and experiments show that RP can yield results comparable to PCA with much less computational cost. Among the 18 algorithms listed in Table 1, only DBA has formally incorporated the notion of sufficiency.
Summary of existing supervised linear dimension reduction algorithms reviewed in Section 2
Iterative Non-iterative Likelihood HDA [29] and [30], MLLT [31], MDA [32], NDA [33] LDA [28], PDA [34]
Error bound orMMI [18] and [35], DFE [15], error integral [16], aPAC [36], error approximation k-NN estimate [7], Patrick–Fisher distance [14], DBA [19] Kullback divergence, Bhattachayya distance [17]
OtherF-LDA [37] NDA [38], RP [39]
This section serves two purposes: (1) to formulate the concept of sufficient subspace for classification in rigorous mathematical form, and (2) to reveal the potential parallelism between classification and regression on the common problem of sufficient dimension reduction. To these ends, we closely follow the recent work of Cook and Li (2002) [40].
Consider a Q-class classification problem with the underlying joint
distribution P(x,y),
where ![]() is a d-dimensional random vector
(feature), and
is a d-dimensional random vector
(feature), and ![]() is a discrete-valued random variable (class label). Let U be a
is a discrete-valued random variable (class label). Let U be a ![]() ,
matrix,
,
matrix, ![]() be
the subspace of
be
the subspace of ![]() spanned by the m column vectors of U. The notion of u
spanned by the m column vectors of U. The notion of u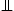 v|z is used to represent the conditional independence
between random vectors u and v
given random vector z.
v|z is used to represent the conditional independence
between random vectors u and v
given random vector z.
We are interested in finding the linear mapping U such that ![]() contains the same amount of discriminative information as
contains the same amount of discriminative information as ![]() .
In the general case, this discriminative information can be characterized by the
expected Bayes risk r given a loss matrix C=[cjk]Q×Q
as
.
In the general case, this discriminative information can be characterized by the
expected Bayes risk r given a loss matrix C=[cjk]Q×Q
as
Definition 1
If y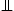 x|UTx, then
x|UTx, then ![]() is
a Bayes sufficient discriminative subspace (BSDS) for the P(x,y)
classification problem.
is
a Bayes sufficient discriminative subspace (BSDS) for the P(x,y)
classification problem.
The next proposition gives equivalent conditions for the conditional independence used in Definition 1.
Proposition 3.1
The following two statements are equivalent:
The definition is equivalent to saying that all the points x that are
mapped into a point ![]() should have the same a posteriori probability distribution P(y|UTx),
which implies that the d×1
feature vector x can be replaced by the m×1
vector UTx
without increasing the expected Bayes risk. Let
should have the same a posteriori probability distribution P(y|UTx),
which implies that the d×1
feature vector x can be replaced by the m×1
vector UTx
without increasing the expected Bayes risk. Let ![]() denote the smallest BSDS. We call
denote the smallest BSDS. We call ![]() Bayes intrinsic discriminative subspace (BIDS), and
Bayes intrinsic discriminative subspace (BIDS), and ![]() Bayes intrinsic discriminative dimension (BIDD).
Bayes intrinsic discriminative dimension (BIDD).
In many cases we are only concerned with the Bayes error ε, which equals the Bayes risk with 0–1 loss:
Definition 2
If y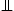 f(x)|UTx, then
f(x)|UTx, then ![]() is a sufficient discriminative subspace (SDS) for the P(x,y)
classification problem.
is a sufficient discriminative subspace (SDS) for the P(x,y)
classification problem.
The next proposition gives equivalent conditions for the conditional independence used in Definition 2.
Proposition 3.2
The following statements are equivalent:
(i) y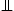 f(x)|UTx,
f(x)|UTx,
(ii) P(y|f(x),UTx)=P(y|UTx),
(iii) f(x) is a function of UTx, i.e., Var(f(x)|UTx)=0.
Let ![]() denote the smallest SDS. We call
denote the smallest SDS. We call ![]() intrinsic discriminative subspace (IDS), and
intrinsic discriminative subspace (IDS), and ![]() intrinsic discriminative dimension (IDD). It follows from Definition
2 that a BSDS is necessarily a SDS, because y
intrinsic discriminative dimension (IDD). It follows from Definition
2 that a BSDS is necessarily a SDS, because y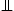 x|UTx implies y
x|UTx implies y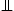 f(x)|UTx. Consequently we
have
f(x)|UTx. Consequently we
have ![]() .
.
As the condition of arbitrary loss function is less common in practice, we will only discuss IDS (under 0–1 loss) in the rest of the paper. The concept of IDS is potentially useful because it represents the maximally possible reduction which is sufficient in the sense that nothing is lost from the original feature space as far as the classification problem is concerned. This knowledge would be valuable for characterizing the intrinsic properties of the data, and for guiding the design of generative models. In practice, however, IDS is not directly available because the underlying joint distribution P(x,y) is unknown. What we have is usually a finite number of samples randomly drawn from this unknown distribution. To make the concept of IDS really useful, we need to answer one important question: How can we estimate IDS from finite samples accurately and efficiently? This is the task of Section 4.
Finally, we should point out that, conceptually, there exists parallelism between sufficient subspaces for classification and those for regression [4], [6] and [40], such as central subspace for BIDS, structural dimension for BIDD, and central mean subspace for IDS. This is so since classification and regression are inherently similar and can be seen as special cases of function approximation. We plan to further investigate their connections in estimation methodologies for sufficient subspaces in our future work.
Given an original feature space of dimension d, one brute-force
procedure to estimate its IDS can be carried out as follows. First solve
d independent reduction problems corresponding to all d possible
subspace dimensions, resulting in a total of d subspaces ![]() ,
each of which is optimized for a particular subspace dimension m. Then
choose one of them as the final estimate via, e.g., hypothesis testing, cross
validation or other model selection techniques. The assumption behind this
procedure is that
,
each of which is optimized for a particular subspace dimension m. Then
choose one of them as the final estimate via, e.g., hypothesis testing, cross
validation or other model selection techniques. The assumption behind this
procedure is that ![]() do cover some good IDS estimate. Therefore each Φm
is required to minimize some criterion function that well approximates or bounds
the Bayes error. Most error-based algorithms reviewed in Section
2 can be readily applied for this purpose. However, this brute-force
approach has an obvious difficulty, i.e., its high computational complexity.
Solving each Φm
involves time-consuming iterative optimization, while the computational burden
increases rapidly with m. The problem will be more severe if the
expensive but necessary cost to guard against local minima is further counted.
Besides complexity, there is a second and less obvious obstacle this approach
would face when the true IDS dimension is high. That is, most error-based
methods depend on density estimation in the reduced subspace, and thus do not
scale well with the output dimension.
do cover some good IDS estimate. Therefore each Φm
is required to minimize some criterion function that well approximates or bounds
the Bayes error. Most error-based algorithms reviewed in Section
2 can be readily applied for this purpose. However, this brute-force
approach has an obvious difficulty, i.e., its high computational complexity.
Solving each Φm
involves time-consuming iterative optimization, while the computational burden
increases rapidly with m. The problem will be more severe if the
expensive but necessary cost to guard against local minima is further counted.
Besides complexity, there is a second and less obvious obstacle this approach
would face when the true IDS dimension is high. That is, most error-based
methods depend on density estimation in the reduced subspace, and thus do not
scale well with the output dimension.
If we are only concerned with the estimation of IDS, computing optimal subspaces for every possible output dimension is unnecessary. DBA is such a technique that generates a set of nested subspaces via eigen-decomposition in which the true IDS is promised, in theory, to be covered. However, previous implementations of DBA suffer from serious sample size problem. To overcome this, we propose a combination of DBA with support vector machines.
For a two class problem, define a discriminant function
1. The number of non-zero eigenvalues, m=dim(Λ), corresponds to the dimension of IDS.
2. The first m eigenvectors of M (i.e., the first m columns of Ψ) provide an orthonormal basis of IDS.
3. The non-zero eigenvalues show how much h(x) varies in each direction.
When given finite samples, M can be replaced by the estimate
In previous nonparametric implementations of DBA [41] and [42], Parzen density estimator and BPNN have been employed to estimate h(x) from finite samples, and normal vectors are numerically approximated by simple differences:
The major limitation of DBA is the accuracy of the decision boundary estimate. Both Parzen density estimator and BPNN have large variance when the original feature dimension is too high. In fact, one of the motivations for dimension reduction is just that we cannot accurately estimate the boundary in high-dimensional space. Another limitation of DBA is the accuracy of normal vector approximation. Numerical gradient calculation might introduce significant noise into the DBSM estimate due to various reasons, such as inappropriate step size, unsmooth local density estimate, bad Parzen scale parameter, and round-off errors. In addition, the numerical approximation is time expensive. To implement the simplest d-dimensional forward differences, h(x) has to be evaluated (d+1) times for each decision surface point.
We propose a multi-class SVM–DBA algorithm. The main idea is to combine DBA with SVM, a powerful kernel-based learning algorithm that has shown potential to break the curse of dimensionality in many applications. The goal is to overcome the difficulty of DBA in small sample size situations, and at the same time keep the simplicity of DBA with respect to IDS estimation.
The decision function of a two-class problem derived by SVM can be written as
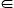 {±1}
is the class label of xi.
A transformation Φ(·)
maps the data points x of the input space
{±1}
is the class label of xi.
A transformation Φ(·)
maps the data points x of the input space 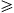 0
are optimized by finding the hyperplane in feature space with maximum distance
to the closest image Φ(xi)
from the training set, which reduces to solving the following linearly
constrained convex quadratic program:
0
are optimized by finding the hyperplane in feature space with maximum distance
to the closest image Φ(xi)
from the training set, which reduces to solving the following linearly
constrained convex quadratic program:The maximum margin boundary provided by SVM has been proven to be optimal in a structural risk minimization sense. Thus we expect that the subspace derived from it through decision boundary analysis can inherit its good generalization performance. However, the small sample size behaviors of most error (or error bound) functionals reviewed in Section 2 do not seem to have been comprehensively investigated.
As the decision boundary of SVM is represented in a closed form by a small number of support vectors, it becomes unnecessary to employ numerical gradient approximation. By computing normal vectors analytically, both the accuracy and the computational efficiency of DBSM estimation are significantly improved.
Given any two points ![]() such that h(z1)h(z2)<0,
a surface point s=αz1+(1-α)z2,α
such that h(z1)h(z2)<0,
a surface point s=αz1+(1-α)z2,α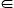 [0,1], can be found by solving the following equation with respect
to α:
[0,1], can be found by solving the following equation with respect
to α:
Commonly used kernel functions and their derivatives, where u and v are d-dimensional vectors
Kernel type K(u,v) ?K(u,v)/?u Linear u·v v Polynomial (u·v+1)p Gaussian radial basis Sigmoid -ηK(u,v)(1-K(u,v))v
Now, we are ready to summarize our multi-class SVM–DBA algorithm as
follows.
| Input: n sample pairs | |
| Output: d nested linear subspaces | |
| Algorithms: | |
S1 |
For k=1 to Q |
| S2 | Divide the n samples into two subsets T+={xi|yi=k} and T-={xi|yi≠k}. Learn a SVM decision function h(x) using T+ and T-. |
| S3 | Sort the n
samples in an ascending order by their absolute function output values |h(xi)|.
Denote the subset consisting of the first r×n
samples as T′,
where 0<r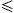 1. 1. |
| S4 | For each z1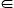 T′, find its nearest neighbor z2 T′, find its nearest neighbor z2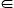 T′ such that T′ such that |
| S5 | Compute the unit
surface norm |
| S6 | End (For k=1 to Q). |
| S7 | Compute the
average scatter matrix |
| S8 | Let |
Summary of dataset information
Dataset #Classes #Features #Samples Benchmark error (%) WAVE-40 3 21+19 — 14 PIMA 2 8 768 22.3 VEHICLE 4 18 846 15.0 LETTER 26 16 20,000 6.4 MFEAT 10 649 2000 2.3
WAVE-40 is a modified version of the simulated example from the CART book. It is a three-class problem with 40 attributes. The first 21 attributes of each class are generated from a combination of two of three “base” waves in Gaussian noise,
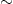 U(0,1) and εi
U(0,1) and εi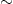 N(0,1). The “base” waves are shifted triangular waveforms:
b1(i)=max(6-|i-1|,0),
b2(i)=b1(i-4),
and b3(i)=b1(i+4).
The remaining 19 attributes of each class are pure Gaussian noise (σ2=9).
N(0,1). The “base” waves are shifted triangular waveforms:
b1(i)=max(6-|i-1|,0),
b2(i)=b1(i-4),
and b3(i)=b1(i+4).
The remaining 19 attributes of each class are pure Gaussian noise (σ2=9).
PIMA consists of 768 medical test records, where the problem is to predict whether a patient would test positive for diabetes. VEHICLE is an ensemble of shape features extracted from 2D silhouettes of 3D vehicle models. LETTER contains image features of 26 English capital letters, which are calculated using edge counts and statistical moments. MEAT consists of handwritten numerals (‘0’–‘9’) extracted from a collection of Dutch utility maps. These digits are represented in terms of six feature sets with a total of 649 attributes.
All these datasets have been extensively benchmarked. Benchmark error rates are listed in the last column of Table 3, including the Bayes error for WAVE-40, the lowest error rates of more than 20 classifiers reported in the StatLog Project for PIMA, VEHICLE and LETTER, and the median error of 25 classifier combination schemes for MFEAT [9].
On each dataset, we compare the goodness of the subspaces induced by SVM–DBA to those by PCA, LDA and DBA [41] (the previous implementation using Parzen density estimator). The experimental setup is summarized in Table 4.
Experimental setup
Dataset (#Training, #Test) p C r λ WAVE-40 (100–1500,5000) 3 0.01–0.6 1.0 0.9 PIMA 12-fold cross validation 2 2–60 0.2 0.04 VEHICLE 9-fold cross validation 5 0.5–60 0.2 0.05 LETTER (15,000, 5000) 5 2–100 0.2 0.005 MFEAT (500,1500) 5 2 0.6 5.0
To help comparison, we have adopted the same evaluation methods as in the benchmark experiments. For WAVE-40, training and test samples are generated independently at random. PIMA and VEHICLE use 12-fold and 9-fold cross-validations respectively, while LETTER and MFEAT use deterministic training/test splits. To help SVM training, all features are linearly normalized into the range of [0,1] before running dimension reduction algorithms.
The degree of polynomial kernel p and the penalty weight C in SVM–DBA, as well as the Parzen scale parameter λ in DBA, are determined via cross-validation on the training data. The ratio r of training samples used to find boundary points in SVM–DBA is set manually.
We employ p-polynomial SVM classifiers to evaluate the feature subspaces generated by PCA, LDA, DBA and SVM–DBA, respectively. Since SVM is presently one of the best classification techniques, it might provide a better index for the discrimination power of the induced subspace. A constant polynomial degree p is used for each dataset, which is the same as in SVM–DBA. However, the penalty C is optimized for different subspaces via cross-validation.
We first illustrate the robustness of SVM–DBA to small sample size on WAVE-40. It can be proven that the Bayes error of WAVE-40 is about 14%, and its IDS dimension equals two. Hence we can generate training sets of different sizes, and directly evaluate the quality of the IDS estimate (i.e., the induced 2D subspaces). The average SVM error over 50 simulations in the estimated IDS is plotted in Fig. 1 as a function of the size of training data. The gap between LDA and SVM–DBA error increases from 1.6% to 11.3% when sample size is reduced from 1500 to 100. The performance of DBA is extremely poor even when the sample size is relatively large, with errors no better than that of random guesses. This confirms that DBA is sensitive to noise. To give an intuitive impression, we show in Fig. 2 the scatter plots of projected training and test samples in the two-dimensional intrinsic discriminative subspaces estimated via different methods.
Fig. 1. Quality of IDS estimation as a function of sample size. SVM classifier is used for evaluation.
(100K)
Fig. 2. Scatter plots of training and test samples from WAVE-40 in the 2D intrinsic discriminative subspaces estimated via different methods. The number of training samples n=500.
We then apply SVM–DBA to the four real-world datasets. Comparative results over all output dimensions are given in Fig. 3. We observe that SVM–DBA is consistently superior on all datasets over a large range of output dimensions. Failures of SVM–DBA at low dimensions are expected, since the optimality of DBA does not hold in subspaces with dimensions less than the true IDS dimension of the data. The drop in SVM error on PIMA suggests that SVM–DBA has introduced further regularizations into SVM for this dataset where there are many irrelevant and/or redundant features. However, similar effects have not been observed with the other three algorithms. Also note that all SVM–DBA error curves are, at some subspace dimensions, lower than or close to the benchmark values. We believe that evaluating the best possible performance of the reduced subspace is meaningful in terms of sufficient dimension reduction.
Fig. 3. Comparison of subspaces over all output dimensions on real-world datasets using SVM classifier.
One may argue that the “good” performance of SVM–DBA can be attributed to the use of the evaluator (i.e., the SVM classifier) itself, and it may work “badly” for other evaluators. To the best of our knowledge, almost all existing linear dimension reduction algorithms can be labeled as so-called filters, and we believe further study on the coupling effect between reduction methods and types of classifiers deserves attention. On the other hand, we believe that there are some common regularities in most real-world datasets that distinguish them from pure random sets, as has been confirmed by the results of other authors [43] and [44]. Hence a subspace that allows high performance of one classifier should also facilitate high performance of a different classifier. As a preliminary attempt, we replace the SVM evaluator with a 1-NN classifier and repeat the comparison of the four reduction algorithms. The results are given in Fig. 4. Although the best performances of 1-NN are much worse than SVM (see Fig. 3) on all datasets except LETTER, the superiority of SVM–DBA is still held. On two datasets (VEHICLE and MFEAT) LDA becomes comparable to SVM–DBA. This can be explained by its “whitening” effect that favors nearest neighbor classification.
Fig. 4. Comparison of subspaces over all output dimensions on real-world datasets using 1-NN classifier.
Finally, we demonstrate the speed-up of SVM–DBA compared to the previous DBA implementation. Shown in Table 5 are the average execution times of all four dimension reduction algorithms (programmed in Matlab) on a Pentium IV 2 GHz PC. We observe that the combination of SVM reduces the computational cost of DBA by at least an order of magnitude. The improvement in efficiency is significant when the feature dimension is high (e.g., MFEAT). Note that DBA was not applied to LETTER, because the sample size is so large that DBA did not terminate after 48 h until we gave up. In another aspect, SVM–DBA provides a way to reduce the run-time complexity of the final classification system. To demonstrate this, we list in Table 6, as an example, the run-time performance of SVM and NN classifiers on MFEAT in typical SVM–DBA subspaces. Note that the SVM time cost is reduced from 9.02 s in the original feature space to 0.72 s in the 15-dimensional subspace with a minor increase in error. For the same subspace, the time cost of NN is reduced from 40.2 to 4.06 s with a 15% decrease in error. Similar results have been observed on other datasets.
Average execution times (s) of different dimension reduction algorithms
Dataset PCA LDA SVM–DBA DBA WAVE-40 0.02 0.02 39.2 361 PIMA 0.01 0.01 8.35 81.7 VEHICLE 0.01 0.01 10.3 118 LETTER 0.23 0.30 2363 — MFEAT 3.17 45.8 136 17,373
Table 6.The run-time performance of SVM and NN classifiers on MFEAT, in subspaces induced by SVM–DBA over typical output dimensions
Dimension 15 25 35 45 65 649 Training time (s) 0.94 0.99 0.98 1.02 1.06 2.50 SVM Test time (s) 0.72 0.84 0.88 0.94 0.97 9.08 Error (%) 2.3 2.2 2.2 2.2 2.2 2.2
NNTest time (s) 4.06 4.69 5.67 6.02 6.84 40.2 Error (%) 2.7 3.0 2.8 3.0 3.1 3.2
Our concept formulation in Section 3 is largely inspired by the work of Cook et al. on sufficient dimension reduction for regression [6] and [40]. The rigorous statistical language they used allows us to treat the sufficient dimension reduction problem for classification in a coherent way. We expect our concept formulation to serve as a good starting point for further investigations of parallelism in estimation methodologies between these two similar problems. For example, using SVM–DBA to estimate the central mean subspace is found to be straightforward and promising, since SVM is also recognized as a powerful tool for high-dimensional regression.
DBA itself is by no means a new concept. Our main contribution is using SVM to derive the boundary with the aim of avoiding the curse of dimensionality that original DBA suffers. Thanks to SVM's compact representation, it is possible for us to analytically compute normal vectors, thus significantly reducing both the estimation error and computational expense.
SVM boundary has been used in locally adaptive metric techniques to improve k-NN performance [23] and [25], in which local feature relevance measures are computed from surface normals and a local full-rank transformation is derived for each query. Instead, SVM–DBA tries to globally characterize the discriminative information embedded in the SVM decision boundary and construct a single reduced-rank projection. SVM boundary has also been used to rank features for subset selection [24]. To the best of our knowledge, our use of SVM for linear dimension reduction is novel.
We formulate the concept of sufficient dimension reduction for classification in parallel terms as for regression. A new method is proposed to estimate IDS, the smallest sufficient discriminative subspace for a given classification problem. The main idea is to combine DBA with SVM in order to overcome the difficulty of DBA in small sample size situations, and at the same time keep the simplicity of DBA in regard to IDS estimation. It also achieves a significant gain in both estimation accuracy and computational efficiency over previous DBA implementations. The proposed method can also be seen as a natural way to reduce the run-time complexity of SVM itself.
The main weakness of our method is its exclusive dependence on SVM
performance. Isolating full-dimensional boundary estimation from subspace
projection inevitably results in suboptimal solutions. For a complex problem as
dimension reduction, it would not be wise to anticipate the existence of any
single tool that can outperform all others in every practical situation. Real
world problems generally require a number of passes to the same data, while
different approaches often lead to different structural findings at various
stages. In this sense, SVM–DBA provides a simple yet effective way to explore
the intrinsic discriminative structure of high-dimensional data, and thus may be
used as a pre-processing step before a more elegant iterative approach or
generative model is considered. Future research topics include: (1) close the
loop of SVM boundary estimation and subspace induction by minimizing SVM
generalization bounds, (2) attach prior to the linear mapping structure, and (3)
apply SVM–DBA to central mean subspace estimation. ![]()
[1] A.K. Jain and R.C. Dubes, Algorithms for Clustering Data, Prentice-Hall, Englewood Cliffs, NJ (1988).
[2] J.B. Tenenbaum, V. de Silva and J.C. Langford, A global geometric framework for nonlinear dimensionality reduction, Science 290 (2001) (5500), pp. 2319–2323.
[3] S.T. Roweis and L.K. Saul, Nonlinear dimensionality reduction by locally linear embedding, Science 290 (2001) (5500), pp. 2323–2326.
[4] K.-C. Li, Sliced inverse regression for dimension reduction, J. Am. Stat. Assoc. 86 (1991) (414), pp. 316–327.
[5] K.-C. Li, On principal Hessian directions for data visualization and dimension reduction another application of Stein's lemma, J. Am. Stat. Assoc. 87 (1992) (420), pp. 1025–1039.
[6] R. Cook, Regression Graphics Ideas for Studying Regressions through Graphics, Wiley, New York (1998).
[7] L. Buturovic, Toward Bayes-optimal linear dimension reduction, IEEE Trans. Pattern Anal. Mach. Intell. 16 (1994) (4), pp. 420–424.
[8] K. Fukunaga, Introduction to Statistical Pattern Recognition (second ed.), Academic Press, San Diego, CA (1990).
[9] A. Jain, R. Duin and J. Mao, Statistical pattern recognition a review, IEEE Trans. Pattern Anal. Mach. Intell. 22 (2000) (1), pp. 4–37.
[10] R. Chengalvarayan and L. Deng, HMM-based speech recognition using state-dependent, discriminatively derived transforms on Mel-warped DFT features, IEEE Trans. Speech Audio Process. 5 (1997) (3), pp. 243–256.
[11] M.J.F. Gales, Maximum likelihood multiple subspace projections for hidden Markov models, IEEE Trans. Speech Audio Process. 10 (2002) (2), pp. 37–47.
[12] B. Sch?lkopf, A.J. Smola and K.R. Müller, Nonlinear component analysis as a kernel eigenvalue problem, Neural Comput. 10 (1998) (5), pp. 1299–1319.
[13] S. Mika, G. R?tsch, J. Weston, B. Sch?lkopf, K.R. Müller, Fisher discriminant analysis with kernels, in: Neural Networks for Signal Processing IX, 1999, pp. 41–48.
[14] M. Aladjem, Nonparametric discriminant analysis via recursive optimization of Patrick–Fisher distance, IEEE Trans. Syst. Man Cybern. B 28 (1998) (2), pp. 292–299.
[15] A. Biem, S. Katagiri and B.-H. Juang, Pattern recognition using discriminative feature extraction, IEEE Trans. Signal Process. 45 (1997) (2), pp. 500–504.
[16] R. Lotlikar and R. Kothari, Adaptive linear dimensionality reduction for classification, Pattern Recognition 33 (2000) (2), pp. 185–194.
[17] G. Saon, M. Padmanabhan, Minimum Bayes error feature selection for continuous speech recognition, in: Proceedings of NIPS 13, 2000.
[18] K. Torkkola, Learning discriminative feature transforms to low dimensions in low dimensions, in: Proceedings of NIPS 14, 2001.
[19] C. Lee and D. Landgrebe, Feature extraction based on decision boundaries, IEEE Trans. Pattern Anal. Mach. Intell. 15 (1993) (4), pp. 388–400.
[20] L. Jimenez and D. Landgrebe, Hyperspectral data analysis and supervised feature reduction via projection pursuit, IEEE Trans. Geosci. Remote Sensing 37 (1999) (6), pp. 2653–2667.
[21] M. Hristache, A. Juditski, J. Polzehl and V. Spokoiny, Structure adaptive approach for dimension reduction, Ann. Stat. 29 (2001) (6), pp. 1537–1566.
[22] A. Samarov, Exploring regression structure using nonparametric functional estimation, J. Am. Stat. Assoc. 88 (1993) (423), pp. 836–847.
[23] C. Domeniconi, D. Gunopulos, Adaptive nearest neighbor classification using support vector machines, in: Proceedings of NIPS 14, 2001.
[24] I. Guyon, J. Weston, S. Barnhill and V. Vapnik, Gene selection for cancer classification using support vector machines, Mach. Learn. 46 (2002) (1–3), pp. 389–422.
[25] J. Peng, D. Deisterkamp, H. Dai, LDA/SVM driven nearest neighbor classification, in: Proceedings of CVPR, 2001, pp. 58–64.
[26] G. Donato, M. Bartlett, J. Hager, P. Ekman and T. Sejnowski, Classifying facial actions, IEEE Trans. Pattern Anal. Mach. Intell. 21 (1999) (10), pp. 974–989.
[27] A.M. Martinez and A.C. Kak, PCA versus LDA, IEEE Trans. Pattern Anal. Mach. Intell. 23 (2001) (2), pp. 228–233.
[28] N. Campbell, Canonical variate analysis—a general formulation, Aust. J. Stat. 26 (1984), pp. 86–96.
[29] N. Kumar and A. Andreou, Heteroscedastic discriminant analysis and reduced rank HMMs for improved speech recognition, Speech Commun. 26 (1998) (4), pp. 283–297.
[30] G. Saon, M. Padmanabhan, R. Gopinath, S. Chen, Maximum likelihood discriminant feature spaces, in: Proceedings of ICASSP, vol. 2, 2000, pp. 1129–1132.
[31] R. Gopinath, Maximum likelihood modeling with Gaussian distributions for classification, in: Proceedings of ICASSP, 1998, pp. 661–664.
[32] T. Hastie and R. Tibshirani, Discriminant analysis by Gaussian mixtures, J. Roy. Stat. Soc. B 58 (1996), pp. 158–176.
[33] M. Zhu and T. Hastie, Feature extraction for nonparametric discriminant analysis, J. Comput. Graph. Stat. 12 (2003) (1), pp. 101–120.
[34] T. Hastie, A. Buja and R. Tibshirani, Penalized discriminant analysis, Ann. Stat. 23 (1995), pp. 73–102.
[35] K. Bollacker, J. Ghosh, Linear feature extractors based on mutual information, in: Proceedings of ICPR, 1996, pp. 720–724.
[36] M. Loog, R. Duin and R. Haeb-Umbach, Multiclass linear dimension reduction by weighted pairwise Fisher criteria, IEEE Trans. Pattern Anal. Mach. Intell. 23 (2001) (7), pp. 762–766.
[37] R. Lotlikar and R. Kothari, Fractional-step dimensionality reduction, IEEE Trans. Pattern Anal. Mach. Intell. 22 (2000) (6), pp. 623–627.
[38] K. Fukunaga, Nonparametric discriminant analysis, IEEE Trans. Pattern Anal. Mach. Intell. 5 (1984), pp. 671–678.
[39] S. Dasgupta, Experiments with random projection, in: Proceedings of UAI, Stanford, CA, 2000, pp. 143–151.
[40] R. Cook and B. Li, Dimension reduction for conditional mean in regression, Ann. Stat. 30 (2002) (2).
[41] C. Lee and D. Landgrebe, Decision boundary feature extraction for nonparametric classification, IEEE Trans. Syst. Man Cybern. 23 (1993) (2), pp. 433–444.
[42] C. Lee and D. Landgrebe, Decision boundary feature extraction for neural networks, IEEE Trans. Neural Networks 8 (1997) (1), pp. 75–83.
[43] S. Das, Filters, wrappers and a boosting based hybrid for feature selection, in: Proceedings of ICML, 2001, pp. 74–81.
[44]
T. Ho and M. Basu, Complexity measures of supervised classification problems,
IEEE Trans. Pattern Anal. Mach. Intell. 24 (2002) (3),
pp. 289–300.
![]()
Proof of Proposition 3.1
According to the definition of  ,
(i) implies P(y,x|UTx)=P(y|UTx)P(x|UTx).
On the other hand, from the chain rule we have P(y,x|UTx)=P(y|x,UTx)P(x|UTx).
Since P(y|x,UTx)=P(y|x),
the equivalence between (i) and (ii) follows immediately.
,
(i) implies P(y,x|UTx)=P(y|UTx)P(x|UTx).
On the other hand, from the chain rule we have P(y,x|UTx)=P(y|x,UTx)P(x|UTx).
Since P(y|x,UTx)=P(y|x),
the equivalence between (i) and (ii) follows immediately. 
Proof of Proposition 3.2
That (i) implies (ii) is immediate. That (iii) implies (i) is also immediate, because, if f(x) is a function of UTx, then, given UTx, f(x) is a constant and hence independent of any other random variable. Now let us prove that (ii) implies (iii).
Suppose there exist ![]() such that P(UTx=η)>0
and Var(f|UTx=η)≠0,
then there must exist α,β
such that P(UTx=η)>0
and Var(f|UTx=η)≠0,
then there must exist α,β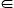 K (α≠β),
such that P(f=α|UTx=η)P(f=β|UTx=η)>0,
or equivalently P(f=α,UTx=η)P(f=β,UTx=η)>0.
According to the definition of f(x),
the inequality
K (α≠β),
such that P(f=α|UTx=η)P(f=β|UTx=η)>0,
or equivalently P(f=α,UTx=η)P(f=β,UTx=η)>0.
According to the definition of f(x),
the inequality

 This
research was supported in part by NIH award N01-CO-07119 and PA-DOH grant
ME01-738.
This
research was supported in part by NIH award N01-CO-07119 and PA-DOH grant
ME01-738.
About the Author—JIAYONG ZHANG received the B.E. and M.S. degrees in Electronic Engineering from Tsinghua University in 1998 and 2001, respectively. He is currently a Ph.D. candidate in the Robotics Institute, Carnegie Mellon University. His research interests include computer vision, pattern recognition, image processing, machine learning, human motion analysis, character recognition and medical applications.
About the Author—YANXI LIU is a faculty member (associate research professor) affiliated with both the Robotics Institute (RI) and the Center for Automated Learning and Discovery (CALD) of Carnegie Mellon University (CMU). She received her Ph.D. in Computer Science from the University of Massachusetts, where she studied the group theory application in robotics. Her postdoct training was in LIFIA/IMAG (now INRIA) of Grenoble, France. She also received an NSF fellowship from DIMACS (NSF Center for discrete mathematics and theoretical computer science). Her research interests include discriminative subspace induction in large biomedical image databases and computational symmetry in robotics, computer vision and computer graphics.