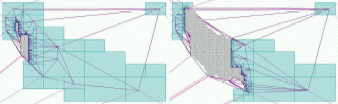
 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Streaming Computation of Delaunay Triangulations,
ACM Transactions on Graphics 25(3):1049-1056, July 2006.
Special issue on Proceedings of SIGGRAPH 2006.
PDF (color, 9,175k, 8 pages).
We compute a billion-triangle terrain representation for the Neuse River
system from 11.2 GB of LIDAR data in 48 minutes using only 70 MB
of memory on a laptop with two hard drives.
This is a factor of twelve faster than the previous fastest
out-of-core Delaunay triangulation software.
We also construct a nine-billion-triangle, 152 GB triangulation in under
seven hours using 166 MB of main memory.
The main new idea in our streaming Delaunay triangulators is
spatial finalization.
We partition space into regions, and include finalization tags
in the stream that indicate when
no more points in the stream will fall in specified regions.
Our triangulators certify triangles or tetrahedra as Delaunay when
the finalization tags show it is safe to do so.
This make it possible to write them out early, freeing up memory
to read more from the input stream.
Because only the unfinalized parts of a triangulation are resident in memory,
the memory footprint remains small.
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Streaming Computation of Delaunay Triangulations,
ACM Transactions on Graphics 25(3):1049-1056, July 2006.
Special issue on Proceedings of SIGGRAPH 2006.
PDF (color, 9,175k, 8 pages).
We compute a billion-triangle terrain representation for the Neuse River
system from 11.2 GB of LIDAR data in 48 minutes using only 70 MB
of memory on a laptop with two hard drives.
This is a factor of twelve faster than the previous fastest
out-of-core Delaunay triangulation software.
We also construct a nine-billion-triangle, 152 GB triangulation in under
seven hours using 166 MB of main memory.
The main new idea in our streaming Delaunay triangulators is
spatial finalization.
We partition space into regions, and include finalization tags
in the stream that indicate when
no more points in the stream will fall in specified regions.
Our triangulators certify triangles or tetrahedra as Delaunay when
the finalization tags show it is safe to do so.
This make it possible to write them out early, freeing up memory
to read more from the input stream.
Because only the unfinalized parts of a triangulation are resident in memory,
the memory footprint remains small.
 Video
plus leaflet:
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Illustrating the Streaming Construction of 2D Delaunay Triangulations,
Proceedings of the Fifteenth Video Review of Computational Geometry
(video) and
Proceedings of the Twenty-Second Annual Symposium on
Computational Geometry (Sedona, Arizona), pages 481-482,
Association for Computing Machinery, June 2006
(leaflet).
PDF (color, 766k, 2 pages).
The
video
(your choice of QT/mpeg4 or DivX)
demonstrates the implementation described in our SIGGRAPH paper (above),
and the leaflet describes the video.
Video
plus leaflet:
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Illustrating the Streaming Construction of 2D Delaunay Triangulations,
Proceedings of the Fifteenth Video Review of Computational Geometry
(video) and
Proceedings of the Twenty-Second Annual Symposium on
Computational Geometry (Sedona, Arizona), pages 481-482,
Association for Computing Machinery, June 2006
(leaflet).
PDF (color, 766k, 2 pages).
The
video
(your choice of QT/mpeg4 or DivX)
demonstrates the implementation described in our SIGGRAPH paper (above),
and the leaflet describes the video.
Talk slides:
Streaming Construction of Delaunay Triangulations.
PDF (color, 2,058k, 96 pages).
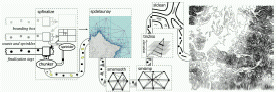
 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, Jack Snoeyink, and
Tim Thirion,
Generating Raster DEM from Mass Points via TIN Streaming,
Proceedings of the Fourth International Conference on
Geographic Information Science
(GIScience 2006, Münster, Germany), September 2006.
PostScript (color, 16,554k, 13 pages).
PDF (color, 490k, 13 pages).
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, Jack Snoeyink, and
Tim Thirion,
Generating Raster DEM from Mass Points via TIN Streaming,
Proceedings of the Fourth International Conference on
Geographic Information Science
(GIScience 2006, Münster, Germany), September 2006.
PostScript (color, 16,554k, 13 pages).
PDF (color, 490k, 13 pages).
 Martin Isenburg, Peter Lindstrom, Stefan Gumhold, and Jonathan Shewchuk,
Streaming Compression of Tetrahedral Volume Meshes,
Proceedings: Graphics Interface 2006 (Quebec City, Quebec, Canada),
pages 115-121, June 2006.
PDF (color, 3,821k, 7 pages).
Martin Isenburg, Peter Lindstrom, Stefan Gumhold, and Jonathan Shewchuk,
Streaming Compression of Tetrahedral Volume Meshes,
Proceedings: Graphics Interface 2006 (Quebec City, Quebec, Canada),
pages 115-121, June 2006.
PDF (color, 3,821k, 7 pages).

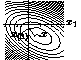 Jonathan Richard Shewchuk,
An Introduction to the Conjugate Gradient Method Without the Agonizing
Pain, August 1994.
Jonathan Richard Shewchuk,
An Introduction to the Conjugate Gradient Method Without the Agonizing
Pain, August 1994.
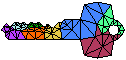 DELAUNAY REFINEMENT MESH GENERATION ALGORITHMS
construct meshes of triangles or tetrahedra (“elements”)
that are suitable for applications like interpolation, rendering,
terrain databases, geographic information systems,
and most demandingly, the solution of partial differential equations
by the finite element method.
Delaunay refinement algorithms operate by maintaining a Delaunay or
constrained Delaunay triangulation which is refined by inserting
additional vertices until the mesh meets constraints
on element quality and size.
These algorithms simultaneously offer theoretical bounds on element quality,
edge lengths, and spatial grading of element sizes;
the ability to triangulate general straight-line domains
(and not just polygons/polyhedra with holes);
and truly satisfying performance in practice.
DELAUNAY REFINEMENT MESH GENERATION ALGORITHMS
construct meshes of triangles or tetrahedra (“elements”)
that are suitable for applications like interpolation, rendering,
terrain databases, geographic information systems,
and most demandingly, the solution of partial differential equations
by the finite element method.
Delaunay refinement algorithms operate by maintaining a Delaunay or
constrained Delaunay triangulation which is refined by inserting
additional vertices until the mesh meets constraints
on element quality and size.
These algorithms simultaneously offer theoretical bounds on element quality,
edge lengths, and spatial grading of element sizes;
the ability to triangulate general straight-line domains
(and not just polygons/polyhedra with holes);
and truly satisfying performance in practice.
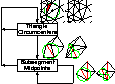 Delaunay Refinement Algorithms for Triangular
Mesh Generation, Computational Geometry:
Theory and Applications 22(1-3):21-74, May 2002.
Delaunay Refinement Algorithms for Triangular
Mesh Generation, Computational Geometry:
Theory and Applications 22(1-3):21-74, May 2002.
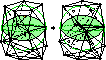 Delaunay Refinement Mesh Generation,
Ph.D. thesis, Technical Report CMU-CS-97-137,
School of Computer Science, Carnegie Mellon
University, Pittsburgh, Pennsylvania, 18 May 1997.
Delaunay Refinement Mesh Generation,
Ph.D. thesis, Technical Report CMU-CS-97-137,
School of Computer Science, Carnegie Mellon
University, Pittsburgh, Pennsylvania, 18 May 1997.
 Tetrahedral Mesh Generation by Delaunay Refinement,
Proceedings of the Fourteenth Annual Symposium on
Computational Geometry (Minneapolis, Minnesota), pages 86-95,
Association for Computing Machinery, June 1998.
Tetrahedral Mesh Generation by Delaunay Refinement,
Proceedings of the Fourteenth Annual Symposium on
Computational Geometry (Minneapolis, Minnesota), pages 86-95,
Association for Computing Machinery, June 1998.
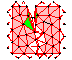 Triangle: Engineering a 2D Quality Mesh
Generator and Delaunay Triangulator,
in Applied Computational Geometry: Towards Geometric Engineering
(Ming C. Lin and Dinesh Manocha, editors),
volume 1148 of Lecture Notes in Computer Science,
pages 203-222, Springer-Verlag (Berlin), May 1996.
From the First Workshop on Applied Computational Geometry
(Philadelphia, Pennsylvania).
Triangle: Engineering a 2D Quality Mesh
Generator and Delaunay Triangulator,
in Applied Computational Geometry: Towards Geometric Engineering
(Ming C. Lin and Dinesh Manocha, editors),
volume 1148 of Lecture Notes in Computer Science,
pages 203-222, Springer-Verlag (Berlin), May 1996.
From the First Workshop on Applied Computational Geometry
(Philadelphia, Pennsylvania).
 François Labelle and Jonathan Richard Shewchuk,
Anisotropic Voronoi Diagrams and
Guaranteed-Quality Anisotropic Mesh Generation,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 191-200,
Association for Computing Machinery, June 2003.
François Labelle and Jonathan Richard Shewchuk,
Anisotropic Voronoi Diagrams and
Guaranteed-Quality Anisotropic Mesh Generation,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 191-200,
Association for Computing Machinery, June 2003.
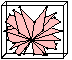 Mesh Generation for Domains with Small Angles,
Proceedings of the Sixteenth Annual Symposium on
Computational Geometry (Hong Kong), pages 1-10,
Association for Computing Machinery, June 2000.
Mesh Generation for Domains with Small Angles,
Proceedings of the Sixteenth Annual Symposium on
Computational Geometry (Hong Kong), pages 1-10,
Association for Computing Machinery, June 2000.
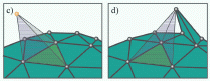
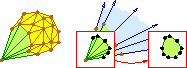 Star Splaying: An Algorithm for Repairing
Delaunay Triangulations and Convex Hulls,
Proceedings of the Twenty-First Annual Symposium on
Computational Geometry (Pisa, Italy), pages 237-246,
Association for Computing Machinery, June 2005.
Star Splaying: An Algorithm for Repairing
Delaunay Triangulations and Convex Hulls,
Proceedings of the Twenty-First Annual Symposium on
Computational Geometry (Pisa, Italy), pages 237-246,
Association for Computing Machinery, June 2005.
 François Labelle and Jonathan Richard Shewchuk,
Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles,
ACM Transactions on Graphics 26(3):57.1-57.10, August 2007.
Special issue on Proceedings of SIGGRAPH 2007.
François Labelle and Jonathan Richard Shewchuk,
Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles,
ACM Transactions on Graphics 26(3):57.1-57.10, August 2007.
Special issue on Proceedings of SIGGRAPH 2007.
 Nuttapong Chentanez, Bryan Feldman, François Labelle,
James O'Brien, and Jonathan Richard Shewchuk,
Liquid Simulation on Lattice-Based Tetrahedral Meshes,
2007 Symposium on Computer Animation (San Diego, California),
pages 219-228, August 2007.
Nuttapong Chentanez, Bryan Feldman, François Labelle,
James O'Brien, and Jonathan Richard Shewchuk,
Liquid Simulation on Lattice-Based Tetrahedral Meshes,
2007 Symposium on Computer Animation (San Diego, California),
pages 219-228, August 2007.
 Bryan Matthew Klingner and Jonathan Richard Shewchuk,
Aggressive Tetrahedral Mesh Improvement,
Proceedings of the 16th International Meshing Roundtable (Seattle, Washington),
pages 3-23, October 2007.
Bryan Matthew Klingner and Jonathan Richard Shewchuk,
Aggressive Tetrahedral Mesh Improvement,
Proceedings of the 16th International Meshing Roundtable (Seattle, Washington),
pages 3-23, October 2007.
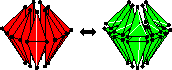 Two Discrete Optimization Algorithms for the
Topological Improvement of Tetrahedral Meshes,
unpublished manuscript, 2002.
Two Discrete Optimization Algorithms for the
Topological Improvement of Tetrahedral Meshes,
unpublished manuscript, 2002.
 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Streaming Computation of Delaunay Triangulations,
ACM Transactions on Graphics 25(3):1049-1056, July 2006.
Special issue on Proceedings of SIGGRAPH 2006.
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,
Streaming Computation of Delaunay Triangulations,
ACM Transactions on Graphics 25(3):1049-1056, July 2006.
Special issue on Proceedings of SIGGRAPH 2006.

 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, Jack Snoeyink, and
Tim Thirion,
Generating Raster DEM from Mass Points via TIN Streaming,
Proceedings of the Fourth International Conference on
Geographic Information Science
(GIScience 2006, Münster, Germany), September 2006.
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, Jack Snoeyink, and
Tim Thirion,
Generating Raster DEM from Mass Points via TIN Streaming,
Proceedings of the Fourth International Conference on
Geographic Information Science
(GIScience 2006, Münster, Germany), September 2006.
 Martin Isenburg, Peter Lindstrom, Stefan Gumhold, and Jonathan Shewchuk,
Streaming Compression of Tetrahedral Volume Meshes,
Proceedings: Graphics Interface 2006 (Quebec City, Quebec, Canada),
pages 115-121, June 2006.
Martin Isenburg, Peter Lindstrom, Stefan Gumhold, and Jonathan Shewchuk,
Streaming Compression of Tetrahedral Volume Meshes,
Proceedings: Graphics Interface 2006 (Quebec City, Quebec, Canada),
pages 115-121, June 2006.
 What Is a Good Linear Finite Element?
Interpolation, Conditioning, Anisotropy, and Quality Measures,
unpublished preprint, 2002.
COMMENTS NEEDED! Help me improve this manuscript.
If you read this, please send feedback.
What Is a Good Linear Finite Element?
Interpolation, Conditioning, Anisotropy, and Quality Measures,
unpublished preprint, 2002.
COMMENTS NEEDED! Help me improve this manuscript.
If you read this, please send feedback.
 What Is a Good Linear Element?
Interpolation, Conditioning, and Quality Measures,
Eleventh International Meshing Roundtable (Ithaca, New York),
pages 115-126, Sandia National Laboratories, September 2002.
What Is a Good Linear Element?
Interpolation, Conditioning, and Quality Measures,
Eleventh International Meshing Roundtable (Ithaca, New York),
pages 115-126, Sandia National Laboratories, September 2002.
 Constrained Delaunay Tetrahedralizations and
Provably Good Boundary Recovery,
Eleventh International Meshing Roundtable (Ithaca, New York),
pages 193-204, Sandia National Laboratories, September 2002.
Constrained Delaunay Tetrahedralizations and
Provably Good Boundary Recovery,
Eleventh International Meshing Roundtable (Ithaca, New York),
pages 193-204, Sandia National Laboratories, September 2002.
 General-Dimensional Constrained Delaunay and
Constrained Regular Triangulations, I: Combinatorial Properties.
Discrete & Computational Geometry 39(1-3):580-637, March 2008.
General-Dimensional Constrained Delaunay and
Constrained Regular Triangulations, I: Combinatorial Properties.
Discrete & Computational Geometry 39(1-3):580-637, March 2008.
 A Condition Guaranteeing the Existence of
Higher-Dimensional Constrained Delaunay Triangulations,
Proceedings of the Fourteenth Annual Symposium on
Computational Geometry (Minneapolis, Minnesota), pages 76-85,
Association for Computing Machinery, June 1998.
A Condition Guaranteeing the Existence of
Higher-Dimensional Constrained Delaunay Triangulations,
Proceedings of the Fourteenth Annual Symposium on
Computational Geometry (Minneapolis, Minnesota), pages 76-85,
Association for Computing Machinery, June 1998.
 Updating and Constructing Constrained Delaunay and
Constrained Regular Triangulations by Flips,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 181-190,
Association for Computing Machinery, June 2003.
Updating and Constructing Constrained Delaunay and
Constrained Regular Triangulations by Flips,
Proceedings of the Nineteenth Annual Symposium on
Computational Geometry (San Diego, California), pages 181-190,
Association for Computing Machinery, June 2003.
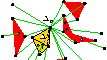 Sweep Algorithms for Constructing
Higher-Dimensional Constrained Delaunay Triangulations,
Proceedings of the Sixteenth Annual Symposium on
Computational Geometry (Hong Kong), pages 350-359,
Association for Computing Machinery, June 2000.
Sweep Algorithms for Constructing
Higher-Dimensional Constrained Delaunay Triangulations,
Proceedings of the Sixteenth Annual Symposium on
Computational Geometry (Hong Kong), pages 350-359,
Association for Computing Machinery, June 2000.
 Nicolas Grislain and Jonathan Richard Shewchuk,
The Strange Complexity of Constrained Delaunay Triangulation,
Proceedings of the Fifteenth Canadian Conference on Computational Geometry
(Halifax, Nova Scotia), pages 89-93, August 2003.
Nicolas Grislain and Jonathan Richard Shewchuk,
The Strange Complexity of Constrained Delaunay Triangulation,
Proceedings of the Fifteenth Canadian Conference on Computational Geometry
(Halifax, Nova Scotia), pages 89-93, August 2003.
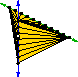 Stabbing Delaunay Tetrahedralizations,
Discrete & Computational Geometry 32(3):339-343, October 2004.
Stabbing Delaunay Tetrahedralizations,
Discrete & Computational Geometry 32(3):339-343, October 2004.
 Ravikrishna Kolluri, Jonathan Richard Shewchuk, and James F. O'Brien,
Spectral Surface Reconstruction from Noisy Point Clouds,
Symposium on Geometry Processing 2004 (Nice, France), pages 11-21,
Eurographics Association, July 2004.
Ravikrishna Kolluri, Jonathan Richard Shewchuk, and James F. O'Brien,
Spectral Surface Reconstruction from Noisy Point Clouds,
Symposium on Geometry Processing 2004 (Nice, France), pages 11-21,
Eurographics Association, July 2004.
 Chen Shen, James F. O'Brien, and Jonathan R. Shewchuk,
Interpolating and Approximating Implicit Surfaces from Polygon Soup,
ACM Transactions on Graphics 23(3):896-904, August 2004.
Special issue on Proceedings of SIGGRAPH 2004.
Chen Shen, James F. O'Brien, and Jonathan R. Shewchuk,
Interpolating and Approximating Implicit Surfaces from Polygon Soup,
ACM Transactions on Graphics 23(3):896-904, August 2004.
Special issue on Proceedings of SIGGRAPH 2004.
 GEOMETRIC PROGRAMS ARE SURPRISINGLY SUSCEPTIBLE
to failure because of floating-point roundoff error.
Robustness problems can be solved by using exact arithmetic,
at the cost of reducing program speed by a factor of ten or more.
Here, I describe a strategy for computing correct answers quickly
when the inputs are floating-point values.
(Much other research has dealt with the problem for integer inputs, which
are less convenient for users but more tractable for robustness researchers.)
GEOMETRIC PROGRAMS ARE SURPRISINGLY SUSCEPTIBLE
to failure because of floating-point roundoff error.
Robustness problems can be solved by using exact arithmetic,
at the cost of reducing program speed by a factor of ten or more.
Here, I describe a strategy for computing correct answers quickly
when the inputs are floating-point values.
(Much other research has dealt with the problem for integer inputs, which
are less convenient for users but more tractable for robustness researchers.)
 Adaptive Precision Floating-Point
Arithmetic and Fast Robust Geometric Predicates,
Discrete & Computational Geometry 18(3):305-363, October 1997.
Adaptive Precision Floating-Point
Arithmetic and Fast Robust Geometric Predicates,
Discrete & Computational Geometry 18(3):305-363, October 1997.
 Robust Adaptive Floating-Point Geometric
Predicates, Proceedings of the Twelfth Annual Symposium on
Computational Geometry (Philadelphia, Pennsylvania), pages 141-150,
Association for Computing Machinery, May 1996.
Robust Adaptive Floating-Point Geometric
Predicates, Proceedings of the Twelfth Annual Symposium on
Computational Geometry (Philadelphia, Pennsylvania), pages 141-150,
Association for Computing Machinery, May 1996.
 PAPERS ABOUT
THE QUAKE PROJECT,
a multidisciplinary Grand Challenge Application
Group studying ground motion in large basins during strong earthquakes,
with the goal of characterizing the seismic response of the Los Angeles basin.
The Quake Project is a joint effort between the departments of Computer Science
and Civil and Environmental Engineering at Carnegie Mellon, the
Southern California Earthquake Center, and the National University of Mexico.
We've created some of the largest unstructured finite element simulations
ever carried out; in particular,
the papers below describe a simulation of ground motion during an
aftershock of the 1994 Northridge Earthquake.
PAPERS ABOUT
THE QUAKE PROJECT,
a multidisciplinary Grand Challenge Application
Group studying ground motion in large basins during strong earthquakes,
with the goal of characterizing the seismic response of the Los Angeles basin.
The Quake Project is a joint effort between the departments of Computer Science
and Civil and Environmental Engineering at Carnegie Mellon, the
Southern California Earthquake Center, and the National University of Mexico.
We've created some of the largest unstructured finite element simulations
ever carried out; in particular,
the papers below describe a simulation of ground motion during an
aftershock of the 1994 Northridge Earthquake.
 Hesheng Bao, Jacobo Bielak, Omar Ghattas, Loukas F. Kallivokas,
David R. O'Hallaron, Jonathan R. Shewchuk, and Jifeng Xu,
Large-scale Simulation of Elastic Wave Propagation in Heterogeneous Media
on Parallel Computers,
Computer Methods in Applied Mechanics and Engineering 152(1-2):85-102,
22 January 1998.
Hesheng Bao, Jacobo Bielak, Omar Ghattas, Loukas F. Kallivokas,
David R. O'Hallaron, Jonathan R. Shewchuk, and Jifeng Xu,
Large-scale Simulation of Elastic Wave Propagation in Heterogeneous Media
on Parallel Computers,
Computer Methods in Applied Mechanics and Engineering 152(1-2):85-102,
22 January 1998.
 Hesheng Bao, Jacobo Bielak, Omar Ghattas, David R. O'Hallaron,
Loukas F. Kallivokas, Jonathan R. Shewchuk, and Jifeng Xu,
Earthquake Ground Motion Modeling on
Parallel Computers, Supercomputing '96 (Pittsburgh, Pennsylvania),
November 1996.
Hesheng Bao, Jacobo Bielak, Omar Ghattas, David R. O'Hallaron,
Loukas F. Kallivokas, Jonathan R. Shewchuk, and Jifeng Xu,
Earthquake Ground Motion Modeling on
Parallel Computers, Supercomputing '96 (Pittsburgh, Pennsylvania),
November 1996.
 OUR SECRET TO PRODUCING such huge unstructured simulations?
With the collaboration of David O'Hallaron, I've written
Archimedes,
a chain of tools for automating the construction of general-purpose
finite element simulations on parallel computers.
In addition to the mesh generators Triangle and Pyramid discussed above,
Archimedes includes Slice,
a mesh partitioner based on geometric recursive bisection;
Parcel, which performs the surprisingly jumbled task of
computing communication schedules and
reordering partitioned mesh data into a format a parallel simulation can use;
and Author, which generates parallel C code from high-level
machine-independent programs
(which are currently written by the civil engineers in our group).
Archimedes has made it possible for the Quake Project
to weather four consecutive changes in parallel architecture
without missing a beat.
The most recent information about Archimedes is contained in the Quake papers
listed above.
See also the
Archimedes page.
OUR SECRET TO PRODUCING such huge unstructured simulations?
With the collaboration of David O'Hallaron, I've written
Archimedes,
a chain of tools for automating the construction of general-purpose
finite element simulations on parallel computers.
In addition to the mesh generators Triangle and Pyramid discussed above,
Archimedes includes Slice,
a mesh partitioner based on geometric recursive bisection;
Parcel, which performs the surprisingly jumbled task of
computing communication schedules and
reordering partitioned mesh data into a format a parallel simulation can use;
and Author, which generates parallel C code from high-level
machine-independent programs
(which are currently written by the civil engineers in our group).
Archimedes has made it possible for the Quake Project
to weather four consecutive changes in parallel architecture
without missing a beat.
The most recent information about Archimedes is contained in the Quake papers
listed above.
See also the
Archimedes page.
 Anja Feldmann, Omar Ghattas, John R. Gilbert, Gary L. Miller,
David R. O'Hallaron, Eric J. Schwabe, Jonathan R. Shewchuk, and Shang-Hua Teng,
Automated Parallel Solution of Unstructured PDE Problems,
unpublished manuscript, June 1996.
Anja Feldmann, Omar Ghattas, John R. Gilbert, Gary L. Miller,
David R. O'Hallaron, Eric J. Schwabe, Jonathan R. Shewchuk, and Shang-Hua Teng,
Automated Parallel Solution of Unstructured PDE Problems,
unpublished manuscript, June 1996.
 Jonathan Richard Shewchuk and Omar Ghattas,
A Compiler for Parallel Finite Element Methods with
Domain-Decomposed Unstructured Meshes,
Proceedings of the Seventh International Conference on Domain
Decomposition Methods in Scientific and Engineering Computing
(Pennsylvania State University), Contemporary Mathematics 180
(David E. Keyes and Jinchao Xu, editors), pages 445-450,
American Mathematical Society, October 1993.
Jonathan Richard Shewchuk and Omar Ghattas,
A Compiler for Parallel Finite Element Methods with
Domain-Decomposed Unstructured Meshes,
Proceedings of the Seventh International Conference on Domain
Decomposition Methods in Scientific and Engineering Computing
(Pennsylvania State University), Contemporary Mathematics 180
(David E. Keyes and Jinchao Xu, editors), pages 445-450,
American Mathematical Society, October 1993.
 Eric J. Schwabe, Guy E. Blelloch, Anja Feldmann, Omar Ghattas,
John R. Gilbert, Gary L. Miller, David R. O'Hallaron,
Jonathan R. Shewchuk, and Shang-Hua Teng,
A Separator-Based Framework for Automated Partitioning and Mapping of
Parallel Algorithms for Numerical Solution of PDEs,
Proceedings of the 1992 DAGS/PC Symposium,
Dartmouth Institute for Advanced Graduate Studies, pages 48-62, June 1992.
Eric J. Schwabe, Guy E. Blelloch, Anja Feldmann, Omar Ghattas,
John R. Gilbert, Gary L. Miller, David R. O'Hallaron,
Jonathan R. Shewchuk, and Shang-Hua Teng,
A Separator-Based Framework for Automated Partitioning and Mapping of
Parallel Algorithms for Numerical Solution of PDEs,
Proceedings of the 1992 DAGS/PC Symposium,
Dartmouth Institute for Advanced Graduate Studies, pages 48-62, June 1992.
 David O'Hallaron, Jonathan Richard Shewchuk, and Thomas Gross,
Architectural Implications of a Family of Irregular Applications,
Fourth International Symposium on High Performance Computer Architecture
(Las Vegas, Nevada), February 1998.
David O'Hallaron, Jonathan Richard Shewchuk, and Thomas Gross,
Architectural Implications of a Family of Irregular Applications,
Fourth International Symposium on High Performance Computer Architecture
(Las Vegas, Nevada), February 1998.
 David R. O'Hallaron and Jonathan Richard Shewchuk,
Properties of a Family of Parallel Finite Element Simulations,
Technical Report CMU-CS-96-141, School of Computer Science,
Carnegie Mellon University, Pittsburgh, Pennsylvania, December 1996.
David R. O'Hallaron and Jonathan Richard Shewchuk,
Properties of a Family of Parallel Finite Element Simulations,
Technical Report CMU-CS-96-141, School of Computer Science,
Carnegie Mellon University, Pittsburgh, Pennsylvania, December 1996.
 Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,
Exploiting Domain Geometry in Analogical Route Planning,
Journal of Experimental and Theoretical Artificial Intelligence
9(4):509-541, October 1997.
Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,
Exploiting Domain Geometry in Analogical Route Planning,
Journal of Experimental and Theoretical Artificial Intelligence
9(4):509-541, October 1997.
 Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,
Route Planning and Learning from Execution,
Working notes from the AAAI Fall Symposium
“Planning and Learning: On to Real Applications”
(New Orleans, Louisiana), pages 58-64, AAAI Press, November 1994.
Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,
Route Planning and Learning from Execution,
Working notes from the AAAI Fall Symposium
“Planning and Learning: On to Real Applications”
(New Orleans, Louisiana), pages 58-64, AAAI Press, November 1994.
 Karen Zita Haigh and Jonathan Richard Shewchuk,
Geometric Similarity Metrics for Case-Based Reasoning,
Case-Based Reasoning: Working Notes from the AAAI-94 Workshop
(Seattle, Washington), pages 182-187, AAAI Press, August 1994.
Karen Zita Haigh and Jonathan Richard Shewchuk,
Geometric Similarity Metrics for Case-Based Reasoning,
Case-Based Reasoning: Working Notes from the AAAI-94 Workshop
(Seattle, Washington), pages 182-187, AAAI Press, August 1994.
