This is only a rough outline of the material that was covered in this lecture.
We began with a review of the Hopfield Content Addressable Memory from the last lecture, illustrating the techique by applying it to problem 2 on the sheet of optional homework problems. The net has only 3 neurons, and is used to store a single pattern (110). By applying the prescription given for determining the weights in terms of the stored patterns, we were able to find the weights, and thus the relation between the inputs to each of the three neurons and the outputs of the other two. (Part a). Then, we applied the iterative procedure for updating the values of V1, V2, and V3, starting with the initial pattern (111), showing how the net converged to the correct output (110). (Part b). Then we calculated the "Energy" for the intial case and the final case, showing that, indeed, it converged to the state of lower energy to get the final result.
The main topic covered was the Hopfield-Tank network. This is described in the assigned reading, the paper: J. Hopfield and D. W. Tank, ``Computing with Neural Circuits: A Model'', Science 233, p. 625 (8 Aug 1986).
In this paper, Hopfield and Tank proposed a method of solving difficult optimization problems that had conflicting constraints. The technique involved bringing the network to a final output state that minimized a "cost" function or "energy" that is of the same form as the energy of the Ising model spin glass that we discussed in the previous lecture.
Spin glass:
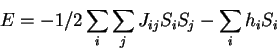
Hopfield-Tank network:
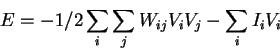
This is like the energy term for a Hopfield CAM, but has an extra term involving the quantity Ii that represents external inputs, bias terms, or a combination of both. Like the CAM, every neuron is connected to every other with symmetric weights, Wij = Wji, and with Wii = 0. With slightly different notation, this is Eq. (2) in the Hopfield-Tank paper.
One difference from the Hopfield CAM, is that the Hopfield-Tank network has continous (analog) values of Vi that are forced toward 0 or 1 by a sigmoidal activation curve. Thus, when the total input to a neuron is large and positive, the output tends towards 1, and it tends towards 0 when the total input is a large negative number. It is this continous value of the Vi's that allows the net to avoid local minima by slowly varying the state of the outputs while converging to a final state.
As with the CAM, for the right kinds of problems, the weights of the Hopfield-Tank network can be determined directly, without the need of training cycles. The idea is to embody the various constraints of the problem into a cost function E of the form given above. The weights Wij and input terms Ii are chosen so that E will be a minimum when the constraints imposed on the outputs are obeyed, and we get the outputs that we want. Like a spin glass, it will be a frustrated system - some constraints will conflict with others, so we will try to get the most optimum energy minimization that we can under the circumstances.
Different external inputs will give different values of the Ii, shifting the shape of the energy surface. Unlike the CAM, in which the desired output state is the local minimum corresponding to the stored pattern that is closest to the intial state, here we want a global minumum. The Wij and Ii have been chosen so that for a given set of Ii (corresponding to a particular input), the energy is a minimum when the net has the desired output for that input.
The network can be implemented either by building an electrical circuit (using operational amplifiers, resistors and capacitors), or by solving a set of differential equations.
The 4-bit analog to digital converter was used in the Hopfield-Tank paper to illustrate this technique. Four "neurons" are reciprocally connected to each other, and to an input source of analog voltage, X. Here, Here 0 <= X < 16, and we want the four Vi's to settle down to binary values that represent the closest integer representation of X. i.e., an approximation to X = 8V3 + 4V2 + 2V2 + V0.
We do this by constructing a cost function that:
The resulting expression is:
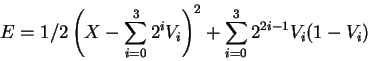
Then, we can find the weights Wij and the parameters
Ii by inspection. It is just a matter of comparing the general
energy expression in Eq. (2) with the specific form in Eq. (3), and finding
the values of Wij that correspond to the coefficients of
ViVj, and the values of Ii that correspond
to the coefficients of Vi. For a given X, the two energy
expressions should be equal (except for an additive constant).
The results were given in Eq. (4) of the paper:
Hopfield and Tank also described an application of this method to the Traveling Salesman Problem. The TSP is a example of a class of difficult optimization problems with conflicting constraints. The object is to choose an itinerary that visits each city exactly once, and that also minimizes the distance traveled. This was done in a similar manner by constructing a cost function that penalizes long paths and those that skip a city or visit a city more than once.
It would be tempting to use strictly binary values for the states Vi of a Hopfield-Tank network. This would seem to be a natural representation for a problem like the A/D converter or others that have a result that is represented by binary values. But, unlike the case of the Hopfield CAM, we need to find the global miniumum of E, not just the nearest local minimum. This presents difficulties for a binary valued Hopfield network, which gives very poor solutions to this kind of problem. We can see this by looking at some plots of energy surfaces. These are easier to visualize if we only have two-dimensions for the inputs and a third for the energy, so the figure here is for a two-bit A/D converter, with the four cases of an input of 0, 1, 2, or 3. The four corners of a surface represent the possible output states of V1V0 = 00, 01, 10, and 11.

For an input voltage of 2, the output state (10) has the lowest energy. If we were to start with a state (00), and change V0 to minimize the energy, we would change it from 0 to 1 and get to the state (01). Then we move on to neuron 1, and see if we should change V1 from 0 to 1. Unfortunately, the state (11) has a higher energy than the state (01), so we leave V1 at 0. When we go back to neuron 0, we find that we cannot reduce the energy any further by changing the value of V0. If we were to change it back to 0, the energy would increase, so we are stuck in the local minimum corresponding to the state (01).
The problem with our procedure is that we are using a "greedy algorithm". We always move in the direction of minimizing the energy, without ever allowing the energy to increase, so that we might later get to a lower minimum. The continuous-valued version of the Hopfield-Tank network avoids this problem by allowing small changes in V0 and V1 that would let us follow a gradual descent from the state (00) to the state (10). If we like the idea of using binary valued neurons instead of ones with analog values, then we need to find another approach.
One very powerful technique is called Simulated Annealing. The idea behind simulated annealing is that instead of being greedy and trying to minimize E by always making changes in the Vi's that minimize E, we find a set of Vi's that is representative of the system at some high temperature, and gradually lower the temperature toward T = 0, where we expect E to be a minimum. This approach is modeled on the process of annealing glass or metals by allowing them to cool slowly after being heated. At high temperatures, the thermal energy allows the atoms (or neurons, in the case of a neural net) to get out of the local minima in energy, so that they can then fall into lower minima. This is possible because at high temperatures, there can be large thermal fluctuations in the energy, which will allow the system to have some probability of increasing its energy as well as decreasing it. As the temperature is lowered, fluctuations in energy become smaller, and it becomes more difficult to leave these lower energy states.
In the case of cooling a molten glass or metal, the temperature T is related to the kinetic energy of motion of the molecules. In a magnetic spin system, T can be related to the distribution of Si's between high and low energy states. (If you have studied statistical thermodynamics, you may recall the Boltzmann distribution, in which the probablility of having an energy E is related to the temperature T.)
The Metropolis Monte Carlo method is an algorithm that can be applied to simulate an Ising model spin glass in thermal equilibrium at a temperature T. It has been used extensively by physicists to study Ising-type magnetic spin systems. Kirkpatrick, Gelatt and Vecchi recognized that the Metropolis algorithm can also be used for the Hopfield-Tank network, or for any optimization problem in which the constraints can be incorporated into a cost function that has the same form as the energy of a spin glass. The steps in the algorithm were given in the handout, but not discussed in class. From the details of the algorithm, it should be apparant that small increases in E are more probable than large ones, and that these increases become less probable as T becomes smaller. The Monte Carlo method is optional material and won't be covered in the exam.
However, we did discuss the application of this method to find a global minimum in the "energy" (or "cost function") of a Hopfield-Tank network. The steps are given in the last part of the handout, "Finding a Global Minimum by Simulated Annealing". When applied to binary valued neural networks or any other system with binary states that has a cost, or "energy" function, the Monte Carlo method is used to bring the system to a state characterized by a temperature T. Then the temperature is gradually lowered, as described above.
For further information about the Metropolis Monte Carlo Method and Simulated Annealing, see: