Neural Network Examples and Demonstrations

Review of Backpropagation

The backpropagation algorithm that we discussed last time is used with a particular network architecture, called a feed-forward net. In this network, the connections are always in the forward direction, from input to output. There is no feedback from higher layers to lower layers. Often, but not always, each layer connects only to the one above.

• It permits the use of the backpropagation algorithm. (This might be a good time to review the description of the backpropagation algorithm from the last lecture.)
• It guarantees that the output will settle down to a steady state when an input is presented. (This does not guarantee that the learning procedure will converge to a solution, however.) When feedback is present, there is the possiblility that an input will cause the network to oscillate.

There are modifications of the backpropagation algorithm for recurrent nets with feedback, but for the general case, they are rather complicated. In the next lecture, we will look at a special case of a recurrent net, the Hopfield model, for which the weights may easily be determined, and which also settles down to a stable state. Although this second property is a very useful feature in a network for practical applications, it is very non-biological. Real neural networks have many feedback connections, and are continually active in a chaotic state. (The only time they settle down to a steady output is when the individual is brain-dead.)

As we discussed in the previous lecture, there are a lot of questions about the backpropagation procedure that are best answered by experimentation. For example: How many hidden layers are needed? What is the optimum number of hidden units? Will the net converge faster if trained by pattern or by epoch? What are the best values of learning rate and momentum to use? What is a "satisfactory" stopping criterion for the total sum of squared errors?

The answers to these questions are usually dependent on the problem to be solved. Nevertheless, it is often useful to gain some experience by varying these parameters while solving some "toy" problems that are simple enough that it is easy to understand and analyze the solutions that are produced by the application of the backpropagation algorithm.

Backpropagation demonstrations

We will start with a demonstration of some simple simulations, using the bp software from the Explorations in Parallel Data Processing book. If you have the software, you might like to try these for yourself. Most of the auxillary files (template files, startup files, and pattern files) are included on the disks in the "bp" directory. For these demos, I've created some others, and have provided links so that they can be downloaded. Appendix C of "Explorations" describes the format of these files.

The XOR network

This is the display that is produced after giving the command

    bp xor2.tem xor2demo.str

and then "strain" (sequential train). The maximum total squared error ("tss") has been set to 0.002 ("ecrit").

epoch   782  tss   0.0020
             gcor  1.0000
cpname  p11  pss   0.0005

              |  weights/biases  |   net_input  |   activation |     delta    |
              |                  |              |              |              |
              |                  |              |              |              |
     OUT      |       -414       |     -379     |        2     |        0     |
     / \      |       /   \      |              |              |              |
    /   \     |     904  -981    |              |              |              |
   /     \    |    /         \   |              |              |              |
  H1     H2   | -289        -679 | 1013     205 |   99      88 |    0       0 |
  | \   / |   |   |  \      / |  |              |              |              |
  |  \ /  |   |  651 651 442 442 |              |              |              |
  |   X   |   |   |     X     |  |              |              |              |
  |  / \  |   |   |    / \    |  |              |              |              |
  IN1   IN2   |                  |              |  100     100 |              |

From the weights and biases, can you figure out what logic function is being calculated by each of the two hidden units? i.e., what "internal representation" of the inputs is being made by each of these units? Can you describe how the particular final values of the weights and biases for the output unit allow the inputs from the hidden units to produce the correct outputs for an exclusive OR?

The 4-2-4 Encoder Network

This network has four input units, each connected to each of the two hidden units. The hidden units are connected to each of four output units.

     OUTPUT         O    O    O    O

     HIDDEN              O    O

     INPUT          O    O    O    O

Input patterns: #1  1    0    0    0
                #2  0    1    0    0
                #3  0    0    1    0
                #4  0    0    0    1

Target (output) patterns: the same

This doesn't do anything very interesting! The motivation for solving such a trivial problem is that it is easy to analyze what the net is doing. Notice the "bottleneck" provided by the layer of hidden units. With a larger version of this network, you might use the output of the hidden layer as a form of data compression.

Can you show that the two hidden units are the minimum number necessary for the net to perform the mapping from the input pattern to the output pattern? What internal representation of the input patterns will be formed by the hidden units?

Let's run the simulation with the command

    bp 424.tem 424demo.str

With ecrit = 0.005, it converged after 973 epochs to give the results:

                          hidden          output layer
                        ----------    -------------------
pattern #1 activations  0.00  0.01    0.97 0.00 0.01 0.01
pattern #2 activations  0.99  0.98    0.00 0.97 0.01 0.01
pattern #3 activations  0.01  0.98    0.01 0.02 0.97 0.00
pattern #4 activations  0.96  0.00    0.01 0.02 0.00 0.97

Another run of the simulation converged after 952 epochs to give:

                          hidden          output layer
                        ----------    -------------------
pattern #1 activations  0.83  0.00    0.97 0.02 0.01 0.00
pattern #2 activations  0.99  0.95    0.01 0.97 0.00 0.01
pattern #3 activations  0.00  0.08    0.02 0.00 0.97 0.01
pattern #4 activations  0.04  0.99    0.00 0.01 0.01 0.97

Are the outputs of the hidden units what you expected? These two simulation runs used different random sets of initial weights. Notice how this resulted in different encodings for the hidden units, but the same output patterns.

The 16 - N - 3 Pattern Recognizer As a final demonstration of training a simple feedforward net with backpropagation, consider the network below.

          1  0  0  0        O
                            O               O
          0  1  0  0        O
                            O               O
          0  0  1  0        .
                            .               O
          0  0  0  1        O

          16 inputs      N hidden       3 output
                      (N = 8, 5, or 3)

The 16 inputs can be considered to lie in a 4x4 grid to crudely represent the 8 characters (\, /, -, |, :, 0, *, and ") with a pattern of 0's and 1's. In the figure, the pattern for "\" is being presented. We can experiment with different numbers of hidden units, and will have 3 output units to represent the 8 binary numbers 000 - 111 that are used to label the 8 patterns. In class, we ran the simulation with 8 hidden units with the command:

    bp  16x8.tem 16x8demo.str

This simulation also used the files 16x8.net, orth8.pat (the set of patterns), and bad1.pat (the set of patterns with one of the bits inverted in each pattern). After the net was trained on this set of patterns, we recorded the output for each of the training patterns in the table below. Then, with no further training, we loaded the set of corrupted patterns with the command "get patterns bad1.pat", and tested them with "tall".

Pattern     Training  output      Testing (1 bad bit in input)
#0  \
#1  /
#2  -
#3  |
#4  :
#5  O
#6  *
#7  "

You may click here to see some typical results of this test. Notice that some of these results for the corrupted patterns are ambigous or incorrect. Can you see any resemblences between the pattern that was presented and the pattern that was specified by the output of the network?

There are a number of other questions that we might also try to answer with further experiments. Would the network do a better or worse job with the corrupted patterns if it had been trained to produce a lower total sum of squared errors? Interestingly, the answer is often "NO". By overtraining a network, it gets better at matching the training set of patterns to the desired output, but it may do a poorer job of generalization. (i.e., it may have trouble properly classifying inputs that are similar to, but not exactly the same as, the ones on which it was trained.) One way to improve the ability of a neural network to generalize is to train it with "noisy" data that includes small random variations from the idealized training patterns.

Another experiment we could do would be to vary the number of hidden units. Would you expect this network to be able discriminate between the 8 different patterns if it had only 3 hidden units? (The answer might surprise you!)

NETtalk

Now, let's talk about an example of a backpropagation network that does something a little more interesting than generating the truth table for the XOR. NETtalk is a neural network, created by Sejnowski and Rosenberg, to convert written text to speech. (Sejnowski, T. J. and Rosenberg, C. R. (1986) NETtalk: a parallel network that learns to read aloud, Cognitive Science, 14, 179-211.)

The problem: Converting English text to speech is difficult. The "a" in the string "ave" is usually long, as in "gave" or "brave", but is short in "have". The context is obviously very important.

A typical solution: DECtalk (a commercial product made by Digital Equipment Corp.) uses a set of rules, plus a dictionary (a lookup table) for exceptions. This produces a set of phonemes (basic speech sounds) and stress assignments that is fed to a speech synthesizer.

The NETtalk solution: A feedforward network similar to the ones we have been discussing is trained by backpropagation. The figure below illustrates the design.

Input layer

has 7 groups of units, representing a "window" of 7 characters of written text. The goal is to learn how to pronounce the middle letter, using the three on either side to provide the context. Each group uses 29 units to represent 26 letters plus punctuation, including a dash for silences. For example, in the group of units representing the letter "c", the third unit is set to "1" and the others are "0". (Question: Why didn't they use a more efficient representation requiring fewer units, such as a binary code for the letters?)

Hidden layer

typically has 80 units, although they tried from 0 to 120 units. Each hidden unit receives inputs from all 209 input units and sends its output to each output unit. There are no direct connections from the input layer to the output layer.

Output layer

has 26 units, with 23 representing different articulatory features used by linguists to characterize speech (voiced, labial, nasal, dental, etc.), plus 3 more to encode stress and syllable boundaries. This output is fed to the final stage of the DECtalk system to drive a speech synthesizer, bypassing the rules and dictionary. (This final stage encodes the output to the 54 phonemes and 6 stresses that are the input to the synthesizer.

Training

was on a 1000 word transcript made from a first grader's recorded speech. (In class we showed this text. Someday, I'll enter it into this web document.) The text is from the book "Informal Speech: Alphabetic and Phonemic Texts with Statistical Analyses and Tables" by Edward C. Carterette and Margaret Hubbard Jones (University of California Press, 1974).

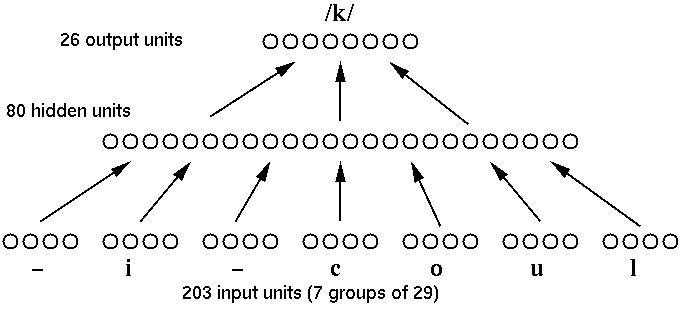
Tape recording The tape played in class had three sections:

1. Taken from the first 5 minutes of training, starting with all weights set to zero. (Toward the end, it begins to sound like speech.)
2. After 20 passes through 500 words.
3. Generated with fresh text from the transcription that was not part of the training set. It had more errors than with the training set, but was still fairly accurate.

I have made MP3 versions of these three sections which you can access as:
nettalk1.mp3 -- nettalk2.mp3 -- nettalk3.mp3

If your browser isn't able to play them directly, you can download them and try them with your favorite MP3 player software.

Here is a link to Charles Rosenberg's web site http://sirocco.med.utah.edu/Rosenberg/sounds.html, where you can access his NETtalk sound files. (NOTE: Your success in hearing these will depend on the sound-playing software used with your web browser. The software that I use produces only static!)

Although the performance is not as good as a rule-based system, it acts very much like one, without having an explicit set of rules. This makes it more compact and easier to implement. It also works when "lobotomized" by destroying connections. The authors claimed that the behaviour of the network is more like human learning than that of a rule-based system. When a small child learns to talk, she begins by babbling and listening to her sounds. By comparison with the speech of adults, she learns to control the production of her vocal sounds. (Question: How much significance should we attach to the fact that the tape sounds like a child learning to talk?)