Overview of artificial neural networks

Sorry! Some of the equations and diagrams are missing in this web version of the lecture!

This is the beginning of a series of lectures on Artificial Neural Nets - often I'll just say "Neural Nets", as most people do. However, if you think that any biologists might be listening, you should be careful to qualify this with the word "artificial". Biologists are easily offended by people who use very simplistic models of interacting neurons and call them "Neural Nets". "Connectionist Computation" is a politically correct expression to use.

Our goal here is to try to identify what sorts of things should go into a simple model of what we might call "biologically-inspired computation". We can't model the brain down to every level of detail, so we have to decide what features are important for the types of computation which are performed by the brain. With any sort of modeling of a complicated system, this question comes up.

Someone once said that if we really wanted biological realism, then airplanes should have feathers. Then, there is the story of the physicist who was going to model a race horse to predict the winner of a horse race. ("First, let us assume a spherical horse ...") We don't want our model to be either an airplane with feathers or a spherical horse. The decision to leave out certain details should be an informed one, not based on ignorance of the details.

A good starting point is to ask how brains differ from present-day computers. Then, we may be able to think of some ways to give computers some of the advantages of brains.

Brains vs. Computers - some differences

Reference: T. Kohonen, Neural Networks 1, 3-16 (1988)

There are some obvious hardware differences -

Brains are massively parallel, with many processing elements (~10¹²) ("fine-grained parallelism") which are highly interconnected ( up to 10,000 connections/neuron). The PE's are slow - time scales are in msec. Analog (and digital in some senses) and asynchronous - no global clock.

Computers are mainly serial devices - even parallel computers have a relatively small number of very complicated PE's with CPU's processing instruction sets, storing things in memory, and so on. ("coarse-grained parallelism") Circuits implemented in silicon or GaAs are very fast - time scales are in nanosec. Digital and synchronous - use clocked logic

The way in which information is stored is probably one of the most significant differences. Computers store "memories" locally in specific memory locations, whereas biological networks appear to use a distributed representation in which a particular memory is stored by a subtle modification of the strengths of very many synaptic connections. Neurobiologists often speak facetiously of a "grandmother cell". This is the neuron which is responsible for recognizing the face of your grandmother. The brain doesn't appear to work that way. If you drink too much and kill a few brain cells, you don't lose the ability to recognize your grandmother, or forget your phone number. Your performance just degrades slightly. Although you won't grow any new neurons, others may take over the job. This fault tolerance of neural circuits is one of their interesting features. (It's true that some neurons perform some very specific functions, however. There are cells in the visual cortex which respond to bars of a certain orientation, moving in a certain direction. This behavior arises out of the properties of the neural circuitry to which they are connected, not because there is anything special about this neuron.) The information stored which enables these "complex cells" to act the way they do is spread over many synaptic connections.

Properties of "wet" neurons

What do we know about the behavior of real neurons which we would like to include in our model?

1. Neurons are integrating (summing) devices. Each input spike causes a PSP which adds to the charge on the membrane capacitance, gradually increasing the membrane potential until the potential in the axon hillock reaches the threshold for firing an action potential. {diagram}

2. Neurons receive both excitatory and inhibitory inputs, with differing and modifiable synaptic weights. This weighting of synaptic inputs can be accomplished in a variety of ways. The efficiency of a single synaptic connection depends on the surface area and geometry of the synapse and the number of vesicles containing neurotransmitter on the presynaptic side. A neuron which interacts strongly with another may make many synapses with the same target neuron, so we can use multiple synapses to increase the weight of a connection between two neurons.

3. Neurons have a non-linear input/output relationship.

              Input                                   Output
   
   |_______|_______|_______|_______|        ________________________________
   
   |___|___|___|___|___|___|___|___|        |_______|_______|_______|_______|
   
   |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|        |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|
   
   |||||||||||||||||||||||||||||||||        |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|
   
   

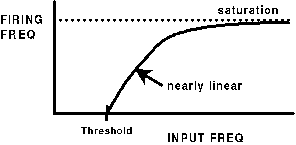
   Do you remember why this is so?

   If we plot the input firing rate vs. the output firing rate, we generally get something like this, with a threshold, and a saturation level arising from the refractory period for firing.

   

The generic model "neuron"

There are many variations on the models which have been proposed for artificial neuron-like computational units. I'll talk about some of them in detail, and a few of them superficially. Most of them have these basic features.

1. The output of the ith neuron is represented by a voltage level, V_i, instead of a sequence of spikes. Sometimes this is a continously variable analog voltage, which represents the firing rate of a real neuron. In other models, the output is a binary value, representing either firing or not firing.

2. The input to the ith neuron is a weighted sum of the outputs of the neurons that make connections to it, plus any external inputs. The connection weights, W_ij, may be positive or negative, representing excitatory or inhibitory inputs.

   

3. The output is related to the input by some non-linear function V_i = f(u_i), which may look like:

   

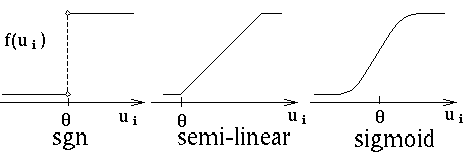
   The function often has some sort of threshold parameter (theta) that allows different neurons to have different thresholds for activation. We'll see different variations on this basic paradigm. Almost all of them have in common the idea that the so-called "neurons" receive inputs from the outside world, or from other neurons, which are multiplied by some weighting factor and summed. The output or "activation" is formed by passing the input through some sort of "squashing" function. This output often becomes the input to other neurons.

We'll be using this notation a lot in the next few lectures, so it would be a good idea to write it down and remember it. That way you won't drown in a sea of meaningless symbols later on. Here is how we would use vector and matrix notation to represent the total input to the ith neuron.

U = W V  + I  {show these as column vectors and a matrix W}

The situation we are describing is something like this,

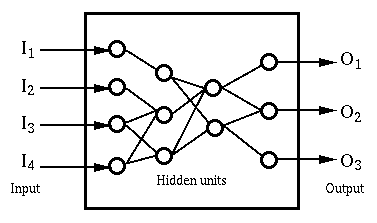
with some units ("neurons") receiving external inputs (I), some presenting an external output (O), and others being intermediate (hidden) units that only connect with other units. The output of one unit is passed on to become part of the weighted input of another, finally reaching the output units. The states of the neurons may be updated in parallel (synchronously), or one at a time (asynchronously). In most neural network models, the network is designed so that the outputs of all the neurons will eventually settle down to a steady state when the external input is held constant. It may take a number of iterations of the update process for this to occur. (Biological networks are different in this respect - their output is usually continously changing.)

Question to discuss: What possibly significant features have we left out of our model? Are there any important ways in which it is different from real neurons?

Spatial effects - What are the consequences of having inputs to various parts of an extended dendritic tree? Can the right weights take this into account? Maybe not. For example, shunting inhibition by the activation of chloride channels close to the soma can "gate" excitation from more distant regions. The various ways that that computations are performed in the dendritic tree is a current research topic.

Temporal effects - is firing rate everything? Our artifical neurons have an output which either corresponds to a firing rate or simply to "firing" or "not firing". However, the pattern of firing of a biological neuron can encode information. The phase relationship and correlations between the firing of neurons can be important. If a neuron receives input from several others that are firing in unison, the effect will be larger than if their firings were uncorrelated. There may be even more subtle ways that the spacing of action potentials can convey information. Consider the differences between the firing patterns of neurons A, B, and C, which all have the same average firing rate:

        A  |___|___|___|___|___|___|___|___|

        B  __|___|___|___|___|___|___|___|__

        C  |||_________|||_________|||______

Here are some specific examples:

    As little as three spikes from the retinal system of the blowfly
    can tell it which way to turn.  [W. Bialek]  Obviously, many bits
    of information would be required for any sort of precision.

    The barn owl uses phase differences and delays for sound
    localization.

    In the cat visual system, spike timing is preserved through four
    layers of the visual cortex - there must be a reason

    Spiral ganglion cells in the cochlea phase lock when stimulated by
    pure tones.

(Some others are listed in L. Watts, Advances in Neural Information
Processing Systems 6 pp. 927-934 (1994))

Learning/plasticity

The knowledge or information content of a neural net is contained in the pattern of connections and the connection strengths. The question then comes up: How do we train a neural net? In biological nets, the mechanisms of "neural plasticity" aren't very well understood, although we know something about conditioned behavior in invertebrates. The changes generally occur as changes in the structure of the synaptic junctions, resulting in changes in the connection strength. During the early stages of development "cell death" is important. This changes the pattern of connections by "pruning" the network of unnecessary or counterproductive neurons. Most algorithms for training artificial neural nets stick with a fixed pattern of connections that the designer feels is appropriate for the problem that the network is expected to solve, and just modify the weights. Any pruning that takes place occurs as a result of some weights approaching zero during the learning process. More recently, there have been attempts to incorporate modification of the connection pattern into the learning algorithm. One class of methods is called "genetic algorithms". The idea is to start with a particular pattern of connectivity and to make random "mutations" or changes in connections, and to keep those which are most successful in terms of some criterion. These then become the starting points for further variations. One approach has the intriguing name of "Optimal Brain Damage". [Le Cun, Denker and Solla, Advances in Neural Information Processing Systems 2, 598 (1989)] The idea here is to start with an excessive number of connections and to train the network in a manner that rewards simplicity over complexity by removing unimportant connections.

At various times, I'll talk about methods of learning that fall into one of three different categories:

1. No learning - "hard-wired" logic - we can figure out what the weights should be for the task at hand and fix them at these values. (e.g. Hopfield nets)

2. Supervised learning - (examples - back propagation, simulated annealing) Example - A net with inputs which correspond to pixel values of a digitized image of the 26 upper case letters A..Z plus maybe 6 other characters. There are 5 neurons whose ouput we monitor, and various other neurons which communicate between the input and output neurons. When we present a character, we want the output neurons to converge to a pattern of 0's and 1's which gives the binary code for the character. This should work even if we have slightly different versions of the letter or it is corrupted by noise. We start with some arbitrary set of weights, present the letter A, and calculate some error term based on the difference between the desired output and the actual output. By some clever technique, we adjust the weights to minimize the error, and then go on to the letter B. After some number of cycles with the whole character set and many slight but hopefully recognizable variations or corruptions of the characters, the net has learned to recognize the 32 characters. If we have done a good job, it will recognize a hand-lettered "E" which it has never seen in the training set. This is a distributed representation - no single neuron or weight represents the letter "E".

   {make a drawing}

3. Unsupervised learning - Kohonen (Self Organizing Maps), Grossberg (Adaptive Resonance Theory) , Zipser (PDP Ch. 5) In this case, we have the same large set of many characters corresponding to slight variations of the 32 characters, but we want the network to find out on its own that they fall into 32 different categories, and to be able to take an input and assign it to the proper category. Not only is this more natural, but for some problems, we don't know the categories. Babies learn like this.

Implementation

How do we build an artificial neural net?

1. Computer simulation on digital computers - currently the most popular method - in the long run, this is not the way to go, but it is a great way to prototype designs and experiment with architectures and learning methods - there are useful commercially sucessful systems which use this method, even though it doesn't exploit the parallelism which is the major advantage of neural nets. If the hardware implementation doesn't need to be able to learn new patterns after its initial training, the training could be carried out and in a computer simulation, and then the final weights can be built into the hardware version.

2. VLSI on silicon Rapid progress is being made in the implementation of neural nets as Very Large Scale Integrated circuits. This holds the most promise in the near future for practical neural networks. It is a mature technology.

   Implementing high connectivity is a problem, because VLSI is essentially two-dimensional. If N neurons are fully interconnected, the number of connections will be N*N. If N = 1000, the area devoted to connections becomes huge, as is the number of crossover connections that need to be made to allow connections on a two-dimensional flat surface.

3. Optical methods The Optoelectronics center here at CU is a major site for research in this area - prospects for practical devices are longer term - the potential is great.

Before getting into the details of some specific neural network models and learning algorithms, there is one more question which we should ask:

What can artificial neural nets do?

I can think of two ways to interpret this question:

1. Given "neurons" which fit this simplified model, what could be computed by a network of arbitrary size and complexity? In principle, could it do anything that the human brain can do? Or does the simplicity of the model limit the capabilities of the network?

2. What are the sorts of problems that are best suited to the SIMPLE neural net architectures which are in use today?

The first question is hard to answer, so I'll dodge it. Maybe we're not ready to answer it until we've seen how far we can push the connectionist model. A simple answer to the second is - "pattern recognition". The problems which are easiest for neural nets are more like low-level "frog intelligence" than high-level human intelligence. However, we need to generalize the idea of pattern recognition beyond just the idea of classifying digitized visual images. The Neurogammon program is a good example. It plays a better game than a rule-based system, without even knowing the rules of the game in the usual sense! It learns by example, and gradually acquires a set of weights which allows it to generalize and make appropriate moves when the input is similar (but not identical) to situations which occurred during the training phase. (In early versions, its average performance was very good, but it would occasionally make a really stupid, off-the-wall move and lose the game. This was because it was confronted with a pattern very unlike any on which it had been trained.) Note that it would be impossible for a net of any reasonable size to "memorize" the response for every conceivable board configuration. This is why it is important for the net to be capable of generalization.

Here are some other typical NN applications:

Optical character recognition is an obvious one, as are military applications involving recognition of digitized images taken from spy satellites and so on. Digitized sonar signals have been presented to a network which can tell the difference between a rock and a metal cylinder of about the same shape. However there are many more subtle forms of pattern recognition.

Interpretation of myocardial perfusion scintigrams - Thallium 201 is used as a radioactive tracer. Experts can visually interpret the images which are produced and detect signs of heart disease, even though the images look nothing like an X-ray or other visual representation of the heart. A neural network was created that compares favorably with human experts (98% success).

Learning the past tense of English verbs (PDP Vol. 2, Ch. 18) This would seem to be the sort of problem best performed by a rule-based system, yet after training, the network did well on both regular and irregular verbs to which it had never been exposed. The sorts of mistakes that it made were very similar to mistakes made by children who were learning to speak.

NETalk (Terry Sejnowski) was in some ways similar. A three-layer feed forward net, took its input from a digital representation of written speech and presented its output to a speech synthesizer which recognized digital codes for phonemes (elementary vocal sounds). During training by back propagation, it would babble like a baby, and gradually become coherent. After training, it did a respectable, but not great, job on text which had never been presented. It has been claimed that its learning paralleled the development of the speech of children. I'll let you decide this for yourselves when I play the tape during another lecture.

Evaluation of mortgage loan applications - There is a successful application of a neural net (simulated on a computer) which is being used by banks to screen loan applications. It is trained by having an expert evaluate the data for a representative set of applications, and give feedback to the net. It works as well as an expert system, but was far easier to implement, because the rules did not have to be spelled out. (There is something ominous about this - if your application is rejected and you ask why, they are likely to say "We can't tell you that". With a human or expert system doing the judging, this isn't strictly true. They don't WANT to tell you. Unfortunately, with a neural net, they are telling the truth!)

There is a neural net that performs medical diagnoses in the field of dermatology, with performance similar to the expert system MYCIN.

Solar flare forecasting - (done at CU - works as well as a human or an expert system, but was far easier to implement)

All of these work by learning a set of connection weights by training from examples. When new inputs that are similar, but not quite the same, are presented, these weights then produce similar outputs.