1
squareĒ_root(x: int)/ok(int) pre
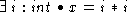
post
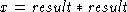
Consider a simpler problem of determining when one binary relation satisfies another. Suppose we have a specification for a square_root procedure:
1
squareĒ_root(x: int)/ok(int) pre
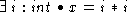
post
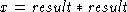
![]()
I could choose to implement this procedure such that I always return the positive square root of an integer. Its relation is:
![]()
Informally, my implementation satisfies the specification
because
![]() just narrows the possible choice of the integer returned
allowed by
just narrows the possible choice of the integer returned
allowed by ![]() and
the implementation defines some value for each input integer
that is defined for the specification.
and
the implementation defines some value for each input integer
that is defined for the specification.
More formally, we have, given an abstract relation, ![]() ,
and a concrete relation,
,
and a concrete relation, ![]() :
:
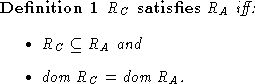
The first property says that any pair in the concrete relation
is also an element of the abstract relation. The second property
says that for each input that is related by ![]() ,
we want
,
we want ![]() to be defined. Without the second property,
to be defined. Without the second property,
![]() could be empty and the satisfies relation would
hold
could be empty and the satisfies relation would
hold![]() .
.