It is common in mathematics to prove an implication ![]() by assuming the antecedent p and proving the consequent q. By
``assuming the antecedent'' we momentarily think of it as an axiom
and thus equivalent to true.
The formal justification of this proof technique relies
on the Deduction Theorem from mathematical logic.
by assuming the antecedent p and proving the consequent q. By
``assuming the antecedent'' we momentarily think of it as an axiom
and thus equivalent to true.
The formal justification of this proof technique relies
on the Deduction Theorem from mathematical logic.![]()
Here is a simple example (from [GS]): Suppose we want to prove
![]() . In the proof we get to assume
the conjuncts of the antecedent. We are required to prove a = b:
. In the proof we get to assume
the conjuncts of the antecedent. We are required to prove a = b:
Proof:
Ass ume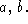
a
= % Assumption of a.
true
= % Assumption of b.
b
Warning:
For the proof of ![]() ,
the Deduction Theorem requires that all variables in the assumed
expression, p, be viewed as constants throughout the proof of q, so
that you cannot substitute expressions in for the ``variables'' that
appear
in the assumptions. The following incorrect proof of
,
the Deduction Theorem requires that all variables in the assumed
expression, p, be viewed as constants throughout the proof of q, so
that you cannot substitute expressions in for the ``variables'' that
appear
in the assumptions. The following incorrect proof of
![]() (which is not valid) shows why
this is necessary. The proof is incorrect because b in the
assumption is replaced.
(which is not valid) shows why
this is necessary. The proof is incorrect because b in the
assumption is replaced.
Proof (Incorrect):
Ass ume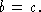
d
= % Assumption of (b = c)[d/b], i.e., d = c
c
Notice that the expression in which we are attempting to do the substitution is b = c.