Step 2

Armed with RI and AF, I can now show the concrete machine satisfies the abstract one.

1. Initial condition.

We need to show that each initial state of Seq maps to some initial state of Set. More formally, we need to show that . This is obviously true by the definition of AF.

2. Commuting diagram for each Seq action.

I need to show this diagram:

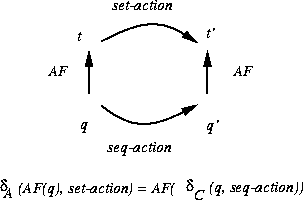
There are five cases, one for each Seq action. I'll just do three actions, addh, remh, and size.

Case: addh satisfies insert.

We'll first consider the case where i is not in the sequence and then the case for when it is.

Case 1:

According to the post-condition for Set's insert action we need to show that the set value for t' obtained after doing an insert with argument i is . Seq's addh action has the effect of adding to the high end of the sequence only if its argument i is not already stored in the sequence. Thus if q is the value of the sequence before, then is the value after. In other words, we have:

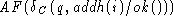
     		post-condition of addh

		  		def'n of AF

		  		since t = AF(q)

		= t'		post-condition of insert

Case 2:

If i is already in the sequence then no state transition occurs and q stays the same.

Case: remh satisfies delete.

According to the post-condition of Set's delete action the set value for t' obtained after doing the delete is the set with i removed. Seq's remh action has the effect of removing and returning the high end of the original sequence q. Informally speaking, it's this element result, which we would ``pass to'' delete as an argument. In other words, given a particular state transition involving remh, I am choosing a particular state transition involving delete--the one for which result is passed as an argument. We have:

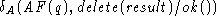
     		post-condition of remh

		  		def'n of AF

		  		post-condition of delete (and def'n of   )

		= AF(q')		properties about set union and set difference

		= t'		t' = AF(q') 

Case: size satisfies card

Looking at the post-condition for Set's card action, there are two things to show.

First, we need to show that the value returned by the Seq's size action is the size of the corresponding set (under AF). Because of NoDups (the RI), we know that the size of the sequence representing a set is the size of the set it represents. More formally, you would need to prove a lemma like:

Second, we need to show that size does not change the abstract value of the set that q represents. More formally,

 q'  = q

  		                             post-condition of size

AF(q') = AF(q)

  				AF is a function.

t'		 = t 

IMPORTANT: Notice that we rely on the abstraction function AF on being a function here. In the second step above, we apply AF to two equal things; since AF is a function (and not a relation), we know the result of applying AF to two equal things will result in two equal things.

For your homework, it's okay to give informal proofs like the ones I give here.