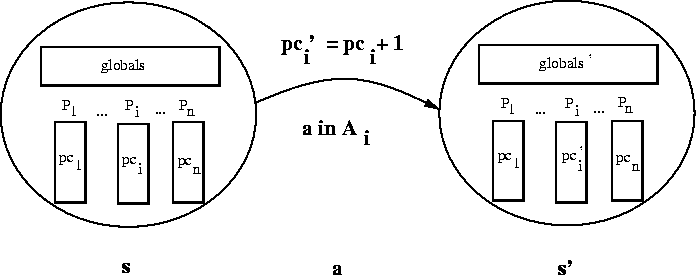Combining State Machines

We first model each process as a (sequential) state machine. Thus, we have and . The question is ``What is an appropriate state machine model for P || Q?'' Before we answer this question, reconsider the example above, where we have (fortuitously) the simpler case that = . You might like a property like:

but that's clearly not true here! That is, there exists a trace in traces(P || Q) that is not even in traces(P) or traces(Q).

What's going on?

1. We need to divide the state variables, , of each process, , into locals and globals. The locals are those that are affected by only that process; the globals are those that are shared with all other processes and can be changed by any of them.
2. For each process, P, we need to add its program counter, , to its set of locals.

Note that we are assuming each state is a mapping from variables to values; here, is the same set as Var in Handout on State Machine Basics for one machine. Since we have more than one process, we need to distinguish between the different variable sets. For simplicity, however, we will assume the same value set, Val, over which all the different types of variables range.

In what follows, to simplify the notation, for state s and variable set V, I'll write to stand for (restriction of the domain of state s to just the variables in V). I'll also write V = V' to stand for (all variables in V stay the same in value).

Now we can define as follows:

• The states:

      = ¯  
  
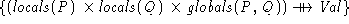
  		where
  
  				  
  
  				  
  
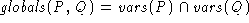
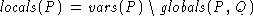
  				  , and
  
  				   
  

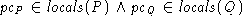
  The sets of locals of each process are mutually disjoint and each set of locals is disjoint with the globals. The intuition is that P can freely change its own locals but not anyone else's and anyone can change any global.

• The initial states:

  The initial states of the composite machine is the set of all states that are initial when projected onto the domain of each of the constituent state machines.

• The actions:

  The set of actions of the composite machine is simply the union of the sets of actions of the constituent state machines. Note that if we tagging each action with a process name, we have . (If we want shared actions, then we would not need to pull this trick of tagging each action.)

• The state transition relation:

      =   ¯  
  
  				  
  
  		  
  
  				   
  

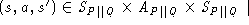
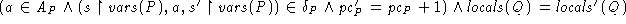
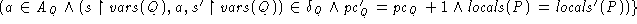
  A step, (s, a, s'), of the composite machine is a step of one of the two machines: if for P, then its pc gets bumped, and all locals of Q stay the same; similarly, if for Q.

  The generalization from two to i processes is straightforward. A picture of a single step transition of a composite machine with i processes looks like the following, where process gets to change the globals as well as its own locals. The locals of all other processes remain the same.