An abstraction function maps a state of the concrete machine to a state of the abstract machine. It explains how to interpret each state of the concrete machine as a state of the abstract machine. It solves the problem of the concrete and abstract machines having different sets of states.
Since the abstraction function is a function, we can rely on the substitution property: If AF is a function and we know x = y then we know AF(x) = AF(y). If AF were a more general kind of relation, this property would not necessarily hold.
You might think that the abstraction function should map the other
way, explaining how to represent each state of the abstract machine.
This is usually not a good idea, in large part because there is often
more than one way of representing each state of the abstract machine.
For example, suppose I represent a set by a sequence. Then
many different sequences, e.g.,
,
,
,
, could (given the appropriate
definition of AF and RI) all represent the same set
.
In other words, AF, in general, is many-to-one.
AF may be partial. Not all states of the concrete machine may represent a ``legal'' abstract state. For example, in the integer-modulo7 example, integers not within 0..6 are not ``legal'' representations of days of the week. The representation invariant serves to restrict the domain of the abstraction function. We may assume that for any concrete state for which the representation invariant does not hold, AF is undefined.
Finally, AF is not necessarily onto. There may be states of the abstract machine that are not represented by any state of the concrete machine. This can be true of initial states as well. In the context of showing that one machine adequately implements another, this may sound strange to you; we say more on adequacy in Section 3.4.
Putting everything together, we have the final diagram:
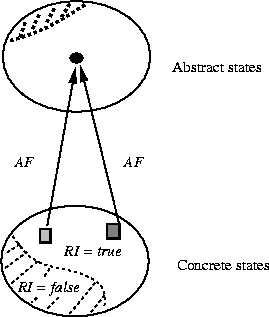
where the bottom unshaded region represents the domain of AF and the top unshaded region represents its range.