A STUDY OF TRUMPET ENVELOPES
Roger B. Dannenberg, Hank Pellerin, and Istvan Derenyi
School of Computer Science, Carnegie Mellon University
Pittsburgh, PA 15213 USA
rbd@cs.cmu.edu, hank.pellerin@andrew.cmu.edu, derenyi@cs.cmu.edu
Abstract: Most synthesis techniques provide for some amount of parametric control. Generating suitable controls is a difficult problem, especially for instruments that admit continuous control by the performer. The traditional approach to control generation in computer music has been note-based, but note-by-note synthesis tends to overlook the interaction between notes in a phrase. This study considers factors, including melodic contour, articulation, and dynamics, that affect the shape of amplitude envelopes in trumpet performance. After showing statistically significant variation due to these factors, a model for trumpet envelopes is described. This model is used with Spectral Interpolation Synthesis to synthesize realistic trumpet performances.
1. Introduction
In our efforts to synthesize the classical trumpet, we have conducted a study of amplitude and frequency envelopes. Previous efforts, originating with Risset (1985), have analyzed individual tones, and resynthesis of individual tones can sound very realistic. When isolated notes are simply joined together, however, the results are neither realistic nor musical. It is important to study and explain the observed variation in envelopes so that musical phrases can be synthesized in a musical manner.
Chafe performed similar studies on strings (Chafe 1989), and Clynes introduced the idea that envelopes change based on local pitch contours and metrical position (Clynes 1987). Sundberg and colleagues created the idea of performance rules (Sundberg, Askenfelt, and Fryden 1983), which can be applied to envelopes, and numerous studies have examined expressive performance. Researchers have also used analysis/synthesis techniques on extended sounds, including musical phrases, and there has been recent interest in relating the analysis to musical structure (Arcos, Mantaras and Serra 1997) and performer’s intention (Canazza, De Poli, and Vidolin 1997). Our approach uses signal analysis and statistics in controlled studies of envelopes.
This study is part of a larger project to explore the use of spectral interpolation in the synthesis of acoustic instrument performances. In this approach, we model an acoustic instrument as a mapping from two or more control parameters (e.g. pitch and amplitude) to a corresponding instantaneous spectrum. (Serra, Rubine, and Dannenberg 1990 and Derenyi and Dannenberg 1998) Realistic, time-varying spectra are produced simply by varying the control parameters. An important challenge in this approach is to produce appropriate control parameters. A simple approach is to capture parameters from acoustic performances, but this is limited to the reproduction of existing sounds. In contrast, the goal of synthesis is to produce new sounds from high-level specifications. In this work, we want to produce sounds from the information typically found in a musical score: notes, slurs, dynamics, and tempo. Therefore, we chose to study envelopes, how they vary, and how their variation might relate to the underlying musical score
This paper presents some of our findings. The next section describes some analytical work in which we applied statistical measures to extracted envelopes. Section 3 discusses the synthesis of envelopes from symbolic score information. Finally, we describe future directions for research, a summary and conclusions.
2. Analysis of Amplitude Envelopes
Our first study was inspired by Clynes’ (1985) envelope model in which the overall "weight" of the envelope is shifted later when the note occurs in a rising pitch contour, and earlier in a falling pitch contour. This makes intuitive sense: The player will increase breath pressure to prepare to move upward, making the latter part of the note louder. The opposite happens with a falling contour. We wanted to study this phenomenon in a controlled experiment and look for other factors that affect envelope shape.
In the experiment, the analyzed note is always the second note in a 3-note contour, and is always an A
I 4 quarter note. The pitches of the first and third notes determine the melodic contour. The first note was either a half step above or below or 5 to 6 half steps above or below the middle note. Similarly, the third note was either a half step above or below, or 5 to 6 half steps above or below the middle note. In addition to varying the contour, we varied the dynamic levels and articulation in hopes of observing the effect of these variables on envelope shape.2.1. Data Collection and Analysis
A set of contours were performed, recorded to DAT, and transferred to sound files for analysis. The A
I 4 tones were manually extracted and analyzed. Since we were already performing spectral analyses with the phase vocoder in the SNDAN program (Beauchamp 1993), we used the RMS amplitude output of SNDAN, normalized to a maximum amplitude of 1, for our envelope data. Each envelope was automatically trimmed, starting when the AI 4 initially crossed a threshold of 0.1 and ending when the subsequent note crossed a threshold of 0.1. The envelopes were then normalized to a duration of 1.0. A total of 125 contours were recorded, varying in interval size, direction, and articulation. 67 of these were performed mezzo forte with "normal" articulation.The center of mass or first moment of each envelope was calculated according to: ![]() .
.
Statistical tests were performed on the centers of mass to see if there was a significant difference between the centers of mass in one category and the centers of mass in another category. The purpose of these tests was to determine whether melodic contour had a significant effect on the shape of the envelopes. Table 1 shows mean center of mass grouped using Tukey’s HSD means test. Different letters indicate that means probably come from significantly different populations (using a 1% risk of error). These tables show that small interval phrases had higher or later mean centers of mass than did large interval phrases, and that, for each size, the up-up contours had significantly higher centers of mass than the other contours.
|
Category |
Mean Center of Mass |
Significant Groupings |
|
Small Interval |
0.443 |
A |
|
Large Interval |
0.409 |
B |
|
Up-Up |
0.448 |
A |
|
Down-Down |
0.425 |
B |
|
Down-Up |
0.417 |
B |
|
Up-Down |
0.415 |
B |
Table 1.
Separation of Means for interval size and contour. All contours played mf with normal articulation.Table 2 shows a similar analysis of the effect of dynamics, and Table 3 shows an analysis of articulation. Note that forte and piano were grouped together with low means and mezzo is a separate group with a high mean center of mass. In Table 3, articulation clearly accounts for large variations in the center of mass.
|
Category |
Mean Center of Mass |
Significant Groupings |
|
mezzo |
0.452 |
A |
|
forte |
0.420 |
B |
|
piano |
0.415 |
B |
Table 2.
Separation of Means for dynamic level.|
Category |
Mean Center of Mass |
Significant Groupings |
|
legato |
0.520 |
A |
|
normal |
0.452 |
B |
|
staccato |
0.313 |
C |
Table 3.
Separation of Means for articulation style.2.2. Discussion of Statistical Results
Overall, these results clearly show that dynamics, articulation, and melodic contour have significant effects upon the shape of the amplitude envelope. Notice that since the envelopes were all normalized in maximum amplitude and duration that it is in fact changes in shape that we are observing. It should be no surprise that articulation has a major impact upon the observed center of mass (compare Figures 1 and 2). Recall that the note duration is taken to be the inter-onset interval, so the silence (if any) following a staccato note is taken to be part of the envelope. Staccato notes are short, so the center of mass is low (early), and legato notes are sustained, so their center of mass is relatively high.
More surprising is the interaction between dynamics and center of mass. Both loud and soft notes show lower centers of mass. We suspect there are two factors at work here. In the case of loud notes, fast attacks are relatively easy to perform using the tongue as a valve to release air suddenly, but sudden stops in the airflow are to be avoided. Perhaps in loud notes, the performer needs more time to reduce the air pressure in preparation for the next note. This would place more of the high amplitude early in the note, thus lowering the center of mass. Soft notes present the player with another problem: attacks are simpler and cleaner with increased air pressure, but this makes the note louder. A solution is to use a relatively loud attack but quickly diminish the sound level. This would also shift the center of mass toward the beginning of the note. It is curious that, after normalization, loud and soft envelopes have similar first moments; more study is called for.
The primary motivation for this study was to look at contour. While the Up-Up contour did in fact have a higher center of mass as expected, Down-Down did not have the lowest, and interval size had a large effect independent of direction. If we assume large intervals are preceded by a slight pause (Sundberg, Askenfelt, and Fryden 1983), then this would lead to a lower center of mass as observed. It is interesting that interval size and melodic direction can act in opposition, an observation which might be helpful in future studies.
3. Synthesizing Envelopes
As described earlier, our goal is to model trumpet (and other) envelopes in order to drive Spectral Interpolation Synthesis. The preceding study shows that there are many parameters affecting the envelope. Many of these parameters can be obtained directly and easily from a symbolic musical score. The hope is that this information is sufficient to synthesize realistic instrumental performances.
By plotting multiple envelopes normalized to unit amplitude and duration, we get a sense for features of envelopes and the nature of variation among envelopes. Overall, we find a very consistent smooth arch shape (see Figure 1). Superimposed upon this curve is a rapid attack, explained by the release of stopped air by the tongue. In consecutive notes, we also observe a short rise followed by a rapid drop at the end of the envelope, all superimposed onto the smooth arch shape. Slurs have a similar dip and rise, but the amplitude does not drop to zero, and the dip is shorter with slurs than in the tongued case (see Figure 2).
3.1. The Breath and Tongue Model
Figure 1 shows a typical trumpet envelope taken from a sequence of tongued quarter notes. This shape can be interpreted based upon some simple elements of trumpet performance. First, the overall arch shape can be attributed to air pressure in the lungs. Since the regulation of this air pressure involves most of the torso, it should not be surprising to find a smooth overall shape as opposed to a rapidly modulated one. The rapid rise is due to the tongue, which acts as a valve in releasing air. As expected, there is much less of this seen in slurred note transitions. We were surprised to see a relatively fast release, almost like that caused by a damper on a piano string, at the end of tongued notes. This can be explained as the effect of stopping air with the tongue in preparation for the next note. In fact, this "damping" feature is not found on notes that are not immediately followed by a tongued note, and it does not appear in classical analyses of the trumpet such as the one by Moorer, Grey, and Strawn (1978).
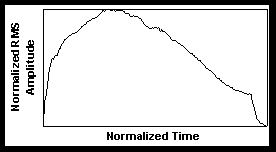 Figure 1. A trumpet envelope for a mezzo forte AI 4 taken from a sequence of ascending tongued notes.
Figure 1. A trumpet envelope for a mezzo forte AI 4 taken from a sequence of ascending tongued notes.
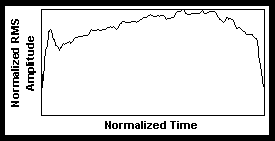 Figure 2. A trumpet envelope for a mezzo forte C4 taken from a sequence of ascending slurred notes.
Figure 2. A trumpet envelope for a mezzo forte C4 taken from a sequence of ascending slurred notes.
Putting these observations together leads to a simple but effective model for trumpet envelopes. A low-rate-of-change curve originating from the chest and diaphragm is combined with high-rate-of-change curves due to the action of the tongue. Overall amplitude is nominally based on pitch, with additional modifications based on dynamic markings. Figure 3 shows an example synthetic envelope illustrating these ideas.
3.2 Fine Tuning
Most of our studies looked at normalized envelopes, so we also looked at variations in absolute amplitude as a function of pitch. Of course, the player has a great deal of control over dynamics, so we analyzed a scale played at a comfortable level. We found an almost linear relationship between RMS amplitude and fundamental frequency , so this forms the basis for overall amplitude.
To this model, we must add some more subtle parameters. We found some variation in shape with duration. Basically, longer notes have a more "rounded" envelope with slowly increasing and decreasing amplitude, indicating the player has more time to "shape" the note with the breath. Shorter notes have a more constant amplitude except where the tongue provides articulation. The general trend of the envelope (increasing or decreasing) is affected by the neighboring pitch contour as described in the previous section.
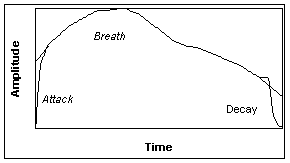 Figure 3. A synthetic envelope showing the "breath" (includes dotted lines) modulated by an attack and decay envelopes. The solid line shows the result.
Figure 3. A synthetic envelope showing the "breath" (includes dotted lines) modulated by an attack and decay envelopes. The solid line shows the result.
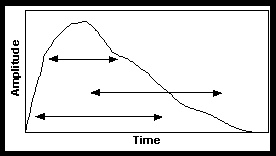
Figure 4. The breath envelope is constructed by extracting a segment, indicated by arrows, of a longer envelope and stretching it to the desired duration.
Based on observations of actual data, we developed a 10-parameter envelope model that incorporates the notion of a breath envelope and tongue envelope. To model the breath, we simply take an actual trumpet envelope (Figure 4), but we extract only a portion (shown by arrows) and stretch that portion to the desired duration. If a small region is taken from the center, the resulting envelope is fairly flat. If a region is taken from earlier or later portions, the resulting envelopes will be generally rising (later center of mass) or falling (earlier center of mass), respectively. Thus, a variety of shapes are available. The resulting "breath envelope" has an instantaneous attack and decay, but these are modified by the "tongue envelope" as described in the next paragraph.
For the tongue envelope, we used analytic functions composed from sines and exponentials, but the functions are fit (by hand) to actual data in order to derive sets of typical parameters. Some of these parameters depend upon context. For example, notes at the end of a phrase have a short release (in this case the breath envelope will be nearly zero), whereas notes preceding a tongued note will have a longer release time that is proportional to the note’s duration. The timings of these features generally vary by only tens of milliseconds, but this small variation has important audible effects, especially at note transitions.
4. Future Work
At the beginning of this study, we had no idea how to think about envelopes in a systematic way, but we began work believing that envelopes are the key to improved music synthesis. It was thus very exciting to discover some simple principles that seem to be effective in envelope synthesis, most importantly the breath and tongue model. This conceptual framework allows us to construct an envelope model with relatively few parameters. This, in turn, should make it possible to use machine learning to construct functions from score parameters to envelope parameters.
Another important direction for future work is to apply these techniques to other instruments. It seems likely that the envelopes of other wind instruments will share many features with those of the trumpet. If so, then it should be possible to make an effective collection of Spectral Interpolation Synthesis wind instruments. This technique may also apply to strings, although there are obvious differences that must be accommodated.
Pitch variation has not received much attention in our work, but vibrato is an especially important area for future study.
5. Summary and Conclusions
We have studied trumpet envelopes as part of a larger effort to create a high-quality synthesizer for the trumpet and other instruments. Statistical analysis of the trumpet shows that the shape of the envelope (not just the amplitude and duration) changes systematically according to melodic context, dynamic level, and articulation. Informed by this study, we created a computer model of trumpet envelopes in which properties of a symbolic score determine a number of envelope parameters. The resulting envelopes are used to drive a Spectral Interpolation Synthesis model, resulting in realistic trumpet phrases. These include appropriate dynamics, spectral variation, tongued attacks, and slurred note transitions. Examples can be found at
http://www.cs.cmu.edu/~rbd/music.An important contribution of this work is an approach in which synthesis is based on phrases rather than individual notes. By looking to melodic contour and other simple features that are readily apparent in the score, we can account for a great deal of variation in envelope shape. This is an important step toward the synthesis of musical phrases.
Acknowledgments
Elizabeth Bunn, at the South Carolina Governor's School for Science and Mathematics, provided assistance with the statistical analysis of trumpet envelopes and served as academic advisor to the second author. Jim Beauchamp provided us with the SNDAN signal analysis tools.
References
Arcos, J. L., R. L. de Mantaras, and X. Serra. 1997. "SaxEx: a case-based reasoning system for generating expressive musical performances," in Proceedings International Computer Music Conference 1997. San Francisco: International Computer Music Association, pp. 329–336.
Beauchamp, J. 1993. "Unix Workstation Software for Analysis, Graphics, Modification, and Synthesis of Musical Sounds." Audio Engineering Society Preprint, No. 3479 (Berlin Convention, March).
Canazza, S., G. De Poli, A. Roda’, and A. Vidolin. 1997. "Analysis and synthesis of expressive intentions in musical performance." In Proceedings of the International Computer Music Conference 1997. San Francisco: International Computer Music Association, pp. 113–120.
Chafe, C. 1989. "Simulating Performance on a Bowed Instrument." In M. Mathews and J. Pierce (Eds.): Current Directions in Computer Music Research. Cambridge MA: M.I.T. Press, pp. 185–198.
Clynes, M. 1985. "Secrets of Life in Music: Musicality Realised by Computer." In Proceedings of the 1984 International Computer Music Conference, Computer Music Association, pp 225–232. (Note: 1984 proceedings were published in 1985.)
Clynes, M. 1987. "What Can a Musician Learn About Music Performance From Newly Discovered Microstructure Principles (PM and PAS)?" in A. Gabrielsson (Ed.): Action and Perception in Rhythm and Music, pp. 201–233. Publications issued by the Royal Swedish Academy of Music No. 55.
Derenyi, I. and R. B. Dannenberg. 1998. "Synthesizing Trumpet Performances." In Proceedings of the International Computer Music Conference. San Francisco: International Computer Music Association.
Moorer, J. A., J. Grey, and J. Strawn. 1978. "Lexicon of Analyzed Tones (Part III: The Trumpet)." Computer Music Journal 2(2), pp. 23–31.
Risset, J.-C. 1985. "Computer Music Experiments 1964–…." Computer Music Journal 9(1) (Spring), pp. 11–18.
Serra, M.-H., D. Rubine, and R. B. Dannenberg. 1990. "Analysis and Synthesis of Tones by Spectral Interpolation,." Journal of the Audio Engineering Society, 38(3) (March), pp. 111–128.
Sundberg, J., A. Askenfelt, and L. Fryden. 1983. "Musical Performance: A Synthesis-by-Rule Approach." Computer Music Journal 7(1), pp. 37–43.