The substitution of equals for equals rule gives us a method for showing that two expressions are equal:
¯e[a/x]= % a = b
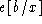
where I wrote the rationalization for the proof step after the % character.
Here is an application of the substitution rule for the rotten apple problem [GS]:
¯
= %
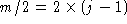
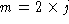
where e is 
,
a is m, and b is 
.
(Notice here that the (boolean) expression
e itself is an equation between two integer
expressions.)
More generally, suppose you want
to prove two expressions, 
and 
, are equal, then
an equational style proof would typically look like:
¯= % explanation of why
= % explanation of why
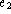
= % explanation of why
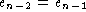
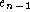
= % explanation of why
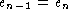
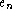
Then we appeal to the transitivity property
of = to conclude that equals
.
The ``explanations'' often appeal to the substitution of equals
for equals rule, but sometimes they appeal to the algebraic
properties of operators that appear in 
. For example,
in the rotten apple problem,
you might find it useful to appeal to the algebraic property
from arithmetic that relates 
and /:
.
Some people prefer to put the explanation on the same line as the ``righthand'' side of the = symbol to save space:
=
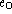
¯% explanation of why
=
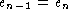
Finally, some people prefer to work with both sides of the equation
at the same time.
At each step in the proof you
find
some subexpression of either the lefthand or righthand side of the
equation
and replace it with an equivalent one; you can keep rewriting both
sides of the equation, justifying each step as before.
You can stop when the expressions on the left and
right
hand sides of the equation are identical (syntactically the same).