I first need to define an abstraction function and a representation invariant.
1. Abstraction Function.
Informally AF takes an (ordered) sequence of elements and turns it into an (unordered) set of the sequence's elements. Formally,
![]()
![]()
![]()
It is common for abstraction functions to be defined recursively like this.
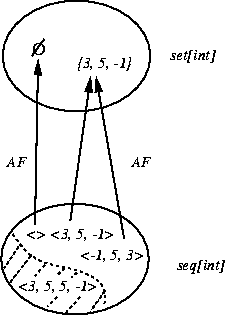
Notice that this AF is many-to-one. There are many sequence values that map to the same set value because we don't care what the order of elements is in a set. In fact, the orderedness property of sequences is exactly the ``irrelevant'' property from which we abstract. For example,
![]()
![]()
![]()
These three different sequence values map to the same set value.
2. Representation Invariant.
Notice that the addh action has a pre-condition that checks whether the element to be inserted is already in the sequence. Thus, only sequence values that have no duplicate elements serve to represent set values. We have the following representation invariant, which characterizes the domain of AF:
![]()
![]()
Informally I'll call this representation invariant, NoDups. Thus we have,
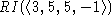
5 appears twice.
= true NoDups
= true The empty sequence is ok.
All those sequence values that RI maps to true are legal representations of set values.
IMPORTANT: Remember that there's a side proof that we need to do here. We need to show that the representation invariant is indeed an invariant. That is, along the lines of the proof technique described in the handout on Reasoning About State Machines, we need to show that the invariant is established in the initial states and preserved by each action. I'll leave this part of the proof as an exercise to the reader.
Here's a picture illustrating that AF is partial and many-to-one: