States Map Variables to Values

 

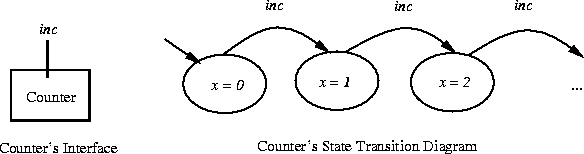
Let's revisit my integer counter example.

In the diagram above, I introduced the variable x to ``hold'' the value of the integer counter. The notion of a state as having variables that can have values of some type should be familiar to you from your programming experience.

With respect to state machine models, what I am doing is refining the notion of what a machine state is; I am adding some internal structure so that states are more than just named entities like 2, off, or crashed. In general, each state in S of a state machine, M, is a finite function from a finite set, Var, of variables (sometimes called ``identifiers'' or ``names'') to a possibly infinite set, Val, of Values:

Moreover, I am going to assume variables and values are typed much like in a programming language. Hence if the variable x is of type int, then I can map it to the integer value ``1'' but not the real value ``3.14159''.

Counter's set of states, S, is a set of total functions mapping x to some integer value:

Since a state is a mapping from variables to values, s(x) denotes the value of the variable x in state s.

Suppose I want to write the state transition function for my Counter? Then, as defined earlier, let S (my set of states) be the set of functions that map the variable x to an integer value. Then similar to the SimpleCounter, I have

Now suppose I have a counter that allows state transitions only from states whose value for its state variable, x, is an even number. EvenCounter starts in the initial state x=0 and whenever I bump its state, I get to the next even number:

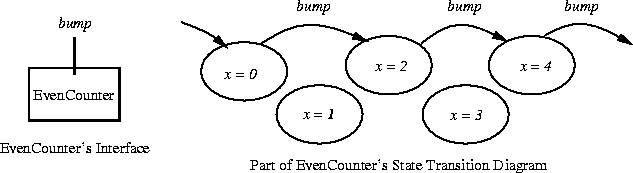
Let EvenCounter's set of states, S, be the same as for Counter. EvenCounter's transition function is:

where we assume the predicate even has been defined appropriately. (Notice that some states in EvenCounter are unreachable. Which ones?)

Unfortunately writing the state transition function as predicates over sets of pairs of states and writing s(x) and/or s'(x) whenever I want to refer to the value of a state variable becomes pretty unwieldy quickly. By introducing two keywords, I will write the state transition function for each action in a more readable notation. Here's what I write for Counter's inc action:

1

 inc pre true

            		post x' = x + 1 

and for EvenCounter's bump action:

1

 bump pre even(x)

            		post x' = x + 2 

The first line, which I'll call the header, gives the name of the action whose state transition behavior I describe in the subsequent two lines. The second line gives a pre-condition, which is just a predicate, and the third line gives a post-condition, which is just another predicate. The interpretation of the pre- and post-conditions is: In order for the state transition to occur from the state s to the state s' the pre-condition must hold in s; after the state transition occurs, then the post-condition must hold in s'. The state transition cannot occur if the pre-condition is not met. Post-conditions in general need to talk about the values of state variables in both the state before the state transition occurs (the ``pre-state'') and the state after it occurs (the ``post-state''). I use an unprimed variable to denote the value of the variable in the pre-state and a primed variable to denote its value in the post-state. So, x' really stands for s'(x); x, for s(x).

Here's how to visualize what the pre- and post-conditions capture:

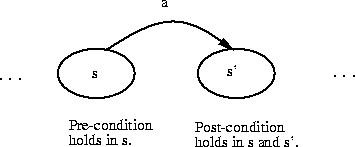
For action a to occur the pre-condition must hold in s. If a occurs, the post-condition must hold in s and s'.

In the Counter example, the inc action has the trivial pre-condition, ``true.'' This means that the inc action can be performed in any state in S. EvenCounter's bump action has a non-trivial pre-condition. Another typical non-trivial pre-condition is requiring that a pop action not be performed on an empty stack. We'll see other examples of non-trivial pre-conditions later. Inc's post-condition says that the value of the integer counter is increased by one from its previous value; bump's post-condition says that the value is increased by two.

In general, for a given , the template I'm using to describe is

1

 actionpre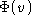   

            		post    

where action is in A, and and are (state) predicates over a vector, v, of state variables. The above template stands for the following part of the definition of the state transition function, :

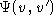
In English this says that the precondition ( ) has to hold in the pre-state and the post-condition ( ) has to hold in the pre/post-states.

Other interpretations of pre/post-condition specifications are possible. I'm just giving you one reasonable one here. For example, another common one is where the conjunction used above is replaced by an implication. Under this interpretation, which is used in Z and Larch, if the pre-condition does not hold and you try to do the action then anything can happen, i.e., ``all bets are off.'' You could end up in an unexpected state, an error state, or an undefined state.