


Next: Example: Active Learning
Up: Active Learning --
Previous: Active Learning --
In this paper we consider algorithms for active learning which select
data in an attempt to minimize the value of
Equation 4, integrated over X. Intuitively, the
minimization proceeds as follows: we assume that we have an estimate
of 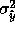 , the variance of the learner at x. If, for
some new input
, the variance of the learner at x. If, for
some new input  , we knew the conditional distribution
, we knew the conditional distribution
 , we could compute an estimate of the
learner's new variance at x given an additional example at
, we could compute an estimate of the
learner's new variance at x given an additional example at
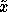 . While the true distribution
. While the true distribution 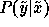 is
unknown, many learning architectures let us approximate it by giving
us estimates of its mean and variance. Using the estimated
distribution of
is
unknown, many learning architectures let us approximate it by giving
us estimates of its mean and variance. Using the estimated
distribution of  , we can estimate
, we can estimate
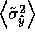 , the expected variance of
the learner after querying at
, the expected variance of
the learner after querying at  .
.
Given the estimate of 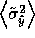 , which
applies to a given x and a given query
, which
applies to a given x and a given query  , we must
integrate x over the input distribution to compute the integrated
average variance of the learner. In practice, we will compute a Monte
Carlo approximation of this integral, evaluating
, we must
integrate x over the input distribution to compute the integrated
average variance of the learner. In practice, we will compute a Monte
Carlo approximation of this integral, evaluating
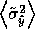 at a number of
reference points drawn according to
at a number of
reference points drawn according to  . By querying an
. By querying an
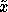 that minimizes the average expected variance over the
reference points, we have a solid statistical basis for choosing new
examples.
that minimizes the average expected variance over the
reference points, we have a solid statistical basis for choosing new
examples.
David Cohn
Mon Mar 25 09:20:31 EST 1996
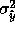 , the variance of the learner at x. If, for
some new input
, the variance of the learner at x. If, for
some new input  , we knew the conditional distribution
, we knew the conditional distribution
 , we could compute an estimate of the
learner's new variance at x given an additional example at
, we could compute an estimate of the
learner's new variance at x given an additional example at
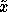 . While the true distribution
. While the true distribution 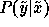 is
unknown, many learning architectures let us approximate it by giving
us estimates of its mean and variance. Using the estimated
distribution of
is
unknown, many learning architectures let us approximate it by giving
us estimates of its mean and variance. Using the estimated
distribution of  , we can estimate
, we can estimate
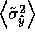 , the expected variance of
the learner after querying at
, the expected variance of
the learner after querying at  .
.



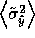 , which
applies to a given x and a given query
, which
applies to a given x and a given query  , we must
integrate x over the input distribution to compute the integrated
average variance of the learner. In practice, we will compute a Monte
Carlo approximation of this integral, evaluating
, we must
integrate x over the input distribution to compute the integrated
average variance of the learner. In practice, we will compute a Monte
Carlo approximation of this integral, evaluating
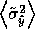 at a number of
reference points drawn according to
at a number of
reference points drawn according to  . By querying an
. By querying an
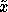 that minimizes the average expected variance over the
reference points, we have a solid statistical basis for choosing new
examples.
that minimizes the average expected variance over the
reference points, we have a solid statistical basis for choosing new
examples.