| 170 | 220 | 110 | 250 |
| 100 | 10 | 230 | 215 |
| 210 | 90 | 60 | 150 |
| 230 | 80 | 120 | 40 |
|
. . |  |
||||||||||||||||
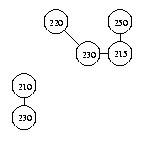
| Example image. | Graph of light pixels. |
The procedure identifies connected components in the graph, and views each component as a separate object. Thus, if we apply it to the above image, it will find two light objects.
Your task is to implement algorithms for identifying connected components of an undirected graph. You should use the source files component.h, component.c, and mycomps.c, along with the old files imageio.h and imageio.c. The component.c file contains the procedure for identifying light objects, which calls three functions from mycomps.c. You should write the code for these functions, called cc_linkedlist, cc_disjointforest, and find_set_df. The mycomps.c file already includes the names and argument declarations for these functions, and you need to code their bodies.
The cc_linkedlist function should use the linked-list representation of disjoint sets to identify connected components, whereas cc_disjointforest should utilize disjoint-set forests. Note that you need to implement Make-Set, Union, and Find-Set, for both linked lists and forests, and use them as subroutines of the connected-component functions. The Union operation for linked lists should always append the shorter list to the longer one, as discussed in class; you may find more information about this technique on page 445 of the textbook, and in Exercise 22.2-1 on page 446. The name of the Find-Set function for disjoint forests should be find_set_df; the header of this function is already in mycomps.c, and you need to write its body. You may choose any names for the other operations on disjoint sets, as they are not called from component.c.
The component.h file contains a structure for representing a node of the graph, called VERTEX. This structure includes the coordinates of the corresponding pixel (called row and col), the adjacency list of the node (called edge), and six elements for disjoint-set operations. The elements representative, nextset, last, and size are for the linked-list implementation, whereas rank and parent are for disjoint-set forests.
The functions in component.c convert the input image into a graph, represented by an array of VERTEX structures, and then call your functions in mycomps.c to identify its connected components. The cc_linkedlist function must ensure that the representative element of each vertex points to the representative in the corresponding component. Similarly, cc_disjointforest needs to set appropriate parent links, which form paths from each vertex to the corresponding representative.
You should not modify any files except mycomps.c, and you should submit only mycomps.c to heath@suntan.eng.usf.edu.
After implementing the connected-component functions, compile component.c and mycomps.c:
gcc -o component component.c mycomps.c imageio.c
You may test your implementation on a very small image, contained in the component.c file, using the "- debug" option:
component -debug
Then, download the stars.pgm file and count stars in this image:
component [-ll | -df] -i stars.pgm -t ###
The first argument specifies whether the procedure uses linked lists (-ll) or disjoint forests (-df); the second argument is the input image; finally, "-t ###" is a threshold value, such as "-t 200". For example, you may use the linked-list implementation, and set the threshold to 200:
component -ll -i stars.pgm -t 200
The procedure displays the number of connected components, graph size (nodes and edges), and execution time. In addition, it produces two output files, called t###.pgm and t###comp.pgm, where ### is the threshold value; for instance, if the threshold is 200, the output files are t200.pgm and t200comp.pgm. The first file is the result of thresholding the image, that is, replacing all pixels above the threshold with 255 (very bright) and all other pixels with 0 (very dark). The other image is the result of "painting" the identified objects with different shades of gray.
You should run the procedure with different thresholds, from 50 to 250; note that the graph size depends on the threshold value, and you can control its size by changing the threshold. First, plot the dependency between the graph size and running time for the linked-list implementation; then, plot a similar dependency for disjoint-set forests. Enclose the graphs to your report, and answer the following questions: