Unit 1

Circuits and Gates

[7.1] How are 1s and 0s represented in the hardware of a computer?

In hardware, bits are represented as electrical voltage. A high level of voltage is considered a 1; a low level of voltage is considered a 0.

[7.2] Why do we need gates? What do they do?

They are abstracted circuit components. They essentially have the same effect as a Boolean operation, but with bits as input/output instead of True/False values where 1 corresponds to True and 0 corresponds to False. They are used to control the flow of information.

[7.3] What is a half adder? Why do we use it? What is a full adder? Why do we use it?

The Half Adder is a type of logic circuit that adds two of the 1-bit binary digits together. When adding two numbers, we might need to carry an output over to the next column of the addition. This is why a half adder is useful. The Full Adder is also a type of logic gate that adds three inputs (3 bits) and produces two outputs. To add multiple bits together we can just chain together the full adder multiple times.

[7.4] What are the three basic gates? How do they operate at the high level?

- An AND gate takes two inputs and outputs 1 only if both inputs were 1.
- An OR gate takes two inputs and outputs 1 if either input was 1.
- A NOT gate takes one input and outputs the reverse (1 becomes 0, 0 becomes 1).

[7.5] Why do we need three representations (boolean expressions, circuits and truth tables)?

All three are different representations of logic; however, the representations for each accomplish a different goal.
-Boolean expressions provide a formal language for expressing logic (i.e., and, or, and not in Python).
-Circuits are concrete implementations of logic using physical or abstract components (i.e., in our CPU).
-Truth tables are a systematic way to analyze and verify the behavior of Boolean expressions or circuits (for our understanding).

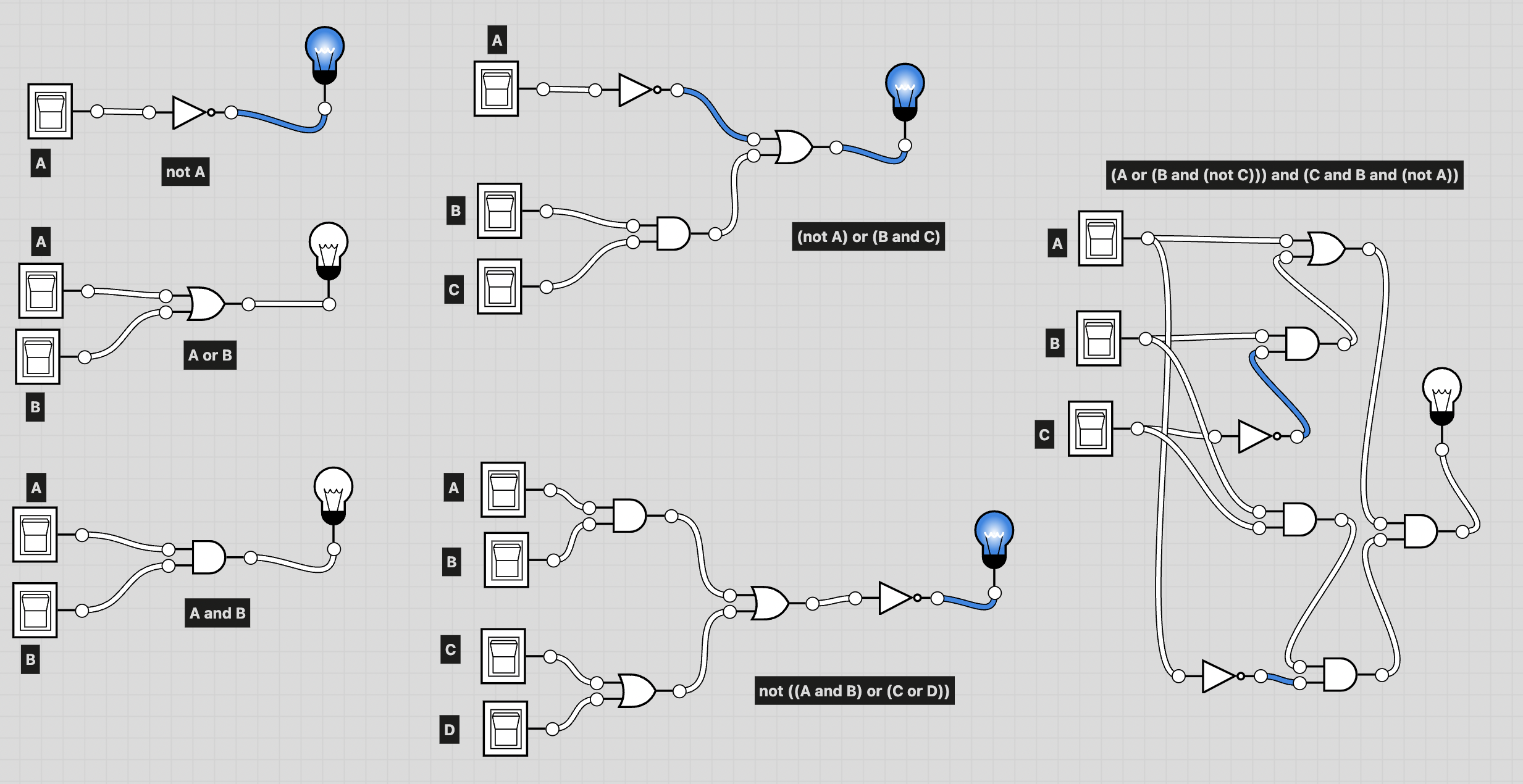
[7.6] Convert the following boolean expressions to truth tables and circuits.

not A
A or B
A and B
(not A) or (B and C)
not ((A and B) or (C or D))

For truth tables, you can use 1/0, or true/false, or T/F

Truth Table: not A

A	not A
true	false
false	true

Truth Table: A or B

A	B	A or B
true	true	true
true	false	true
false	true	true
false	false	false

Truth Table: A and B

A	B	A and B
true	true	true
true	false	false
false	true	false
false	false	false

Truth Table: (not A) or (B and C)

A	B	C	not A	B and C	(not A) or (B and C)
true	true	true	false	true	true
true	true	false	false	false	false
true	false	true	false	false	false
true	false	false	false	false	false
false	true	true	true	true	true
false	true	false	true	false	true
false	false	true	true	false	true
false	false	false	true	false	true

Truth Table: not ((A and B) or (C or D))

A	B	C	D	(A and B) or (C or D)	not ((A and B) or (C or D))
true	true	true	true	true	false
true	true	true	false	true	false
true	true	false	true	true	false
true	true	false	false	true	false
true	false	true	true	true	false
true	false	true	false	true	false
true	false	false	true	true	false
true	false	false	false	false	true
false	true	true	true	true	false
false	true	true	false	true	false
false	true	false	true	true	false
false	true	false	false	false	true
false	false	true	true	true	false
false	false	true	false	true	false
false	false	false	true	true	false
false	false	false	false	false	true

Truth Table: (A or (B and (not C))) and (C and B and (not A))

A	B	C	not C	B and (not C)	A or (B and (not C))	C and B and (not A)	(A or (B and (not C))) and (C and B and (not A))
true	true	true	false	true	true	false	false
true	true	false	true	false	true	false	false
true	false	true	false	false	true	false	false
true	false	false	true	false	true	false	false
false	true	true	false	false	false	false	false
false	true	false	true	false	false	false	false
false	false	true	false	false	false	false	false
false	false	false	true	false	false	false	false

All of the boolean expression above are included in the image below (you can expand)

[7.7] Write the boolean expression and truth table for the circuit below.

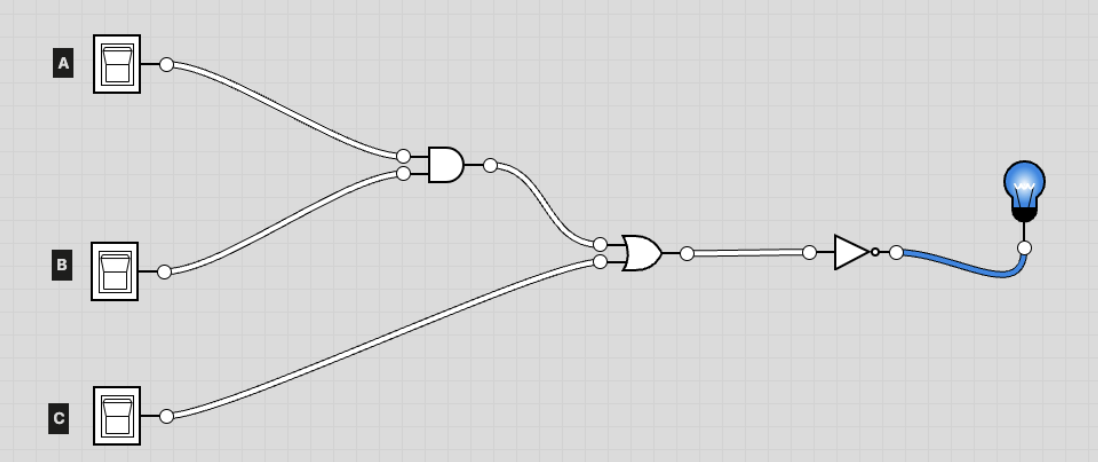
Boolean expression: not ((A and B) or C)

A	B	C	(A and B) or C	not ((A and B) or C)
true	true	true	true	false
true	true	false	true	false
true	false	true	false	true
true	false	false	false	true
false	true	true	true	false
false	true	false	false	true
false	false	true	false	true
false	false	false	true	false

[7.8] Write the boolean expression and truth table for the circuit below.

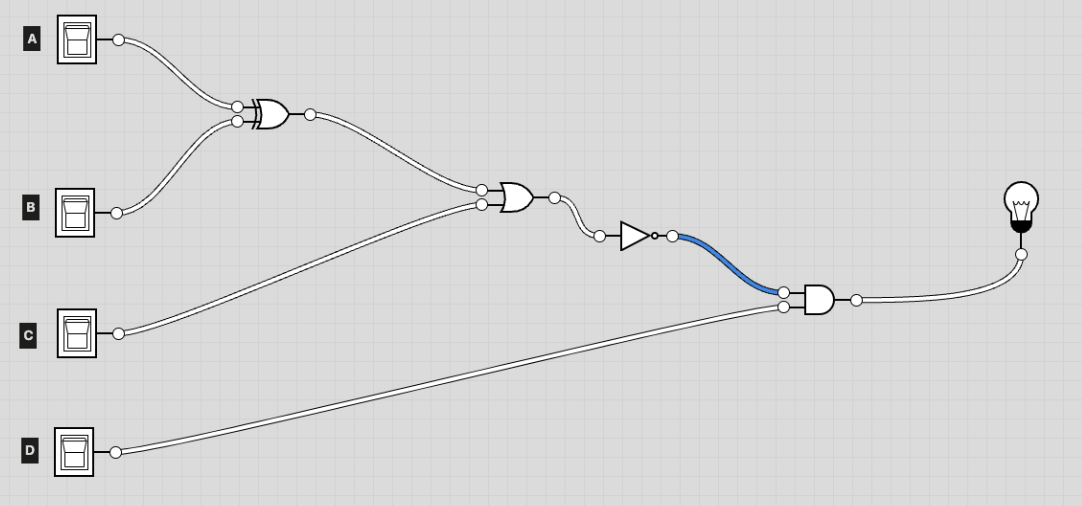
Boolean expression: (not ((A xor B) or C)) and D

A	B	C	D	A xor B	(A xor B) or C	not ((A xor B) or C)	(not ((A xor B) or C)) and D
true	true	true	true	false	true	false	false
true	true	true	false	false	true	false	false
true	true	false	true	true	true	false	false
true	true	false	false	true	true	false	false
true	false	true	true	true	true	false	false
true	false	true	false	true	true	false	false
true	false	false	true	true	true	false	false
true	false	false	false	true	true	false	false
false	true	true	true	true	true	false	false
false	true	true	false	true	true	false	false
false	true	false	true	false	false	true	true
false	true	false	false	false	false	true	true
false	false	true	true	false	true	true	true
false	false	true	false	false	false	true	true
false	false	false	true	false	false	true	true
false	false	false	false	false	false	true	true