Unit 2

[17.1] What is one way in which graphs differ from trees?

[17.2] What are some examples of real-world data that can be represented by graphs?

[17.3] Consider that we want to represent a map as a graph. What would the nodes, edges, and edge weights represent?

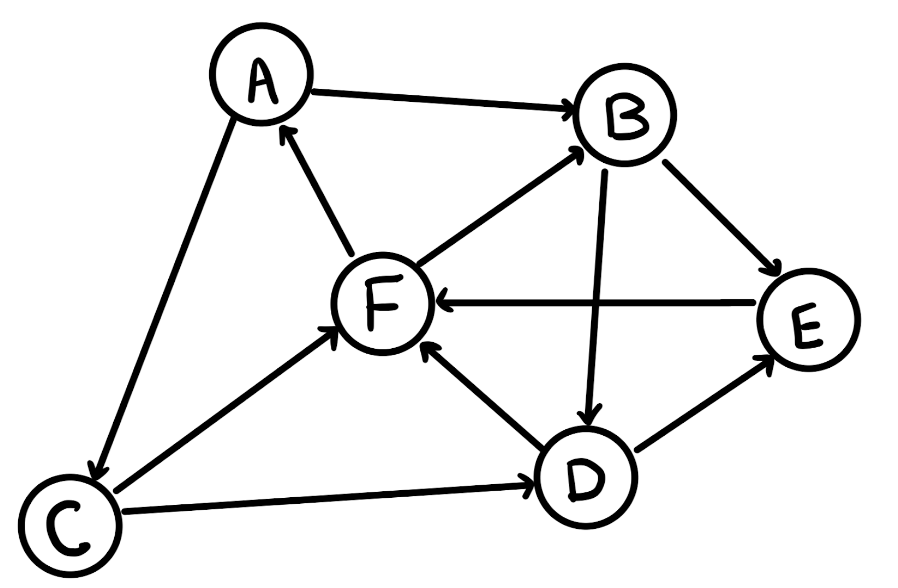
[17.4] Consider the following weighted graph. How many nodes and edges are present in the graph? What are the neighbors of F? What are the neighbors of D? What is the sum of the weights going from D to its neighbors? Is the graph a weighted or unweighted graph? Is it a directed or undirected graph?

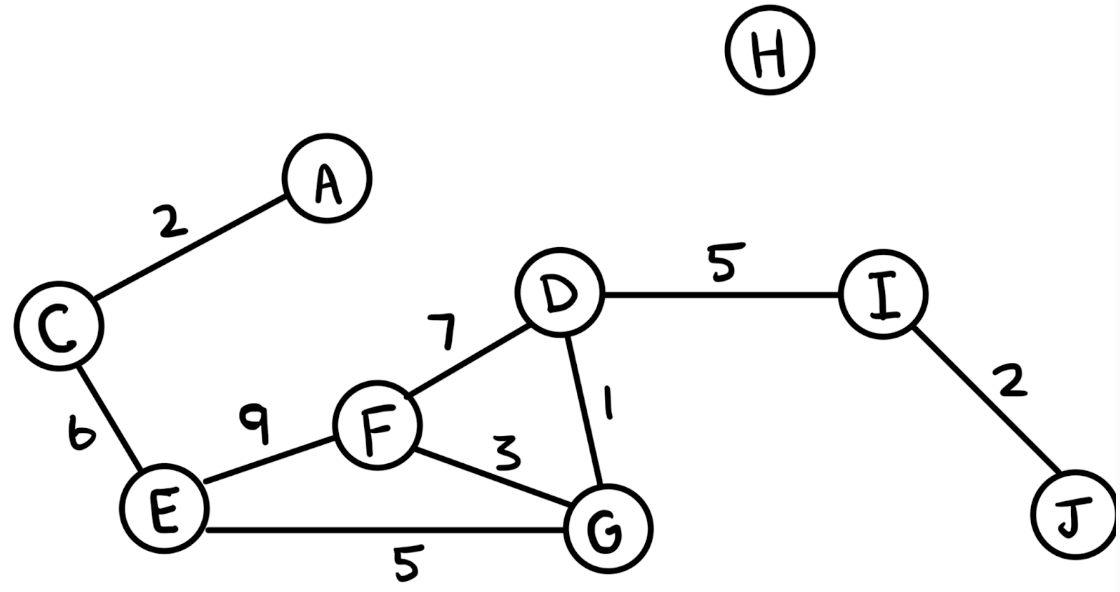
[17.5] Consider the following weighted graph. What are the neighbors of F? What are the neighbors of D? What is the sum of the weights going from D to its neighbors? Is the graph a weighted or unweighted graph? Is it a directed or undirected graph?

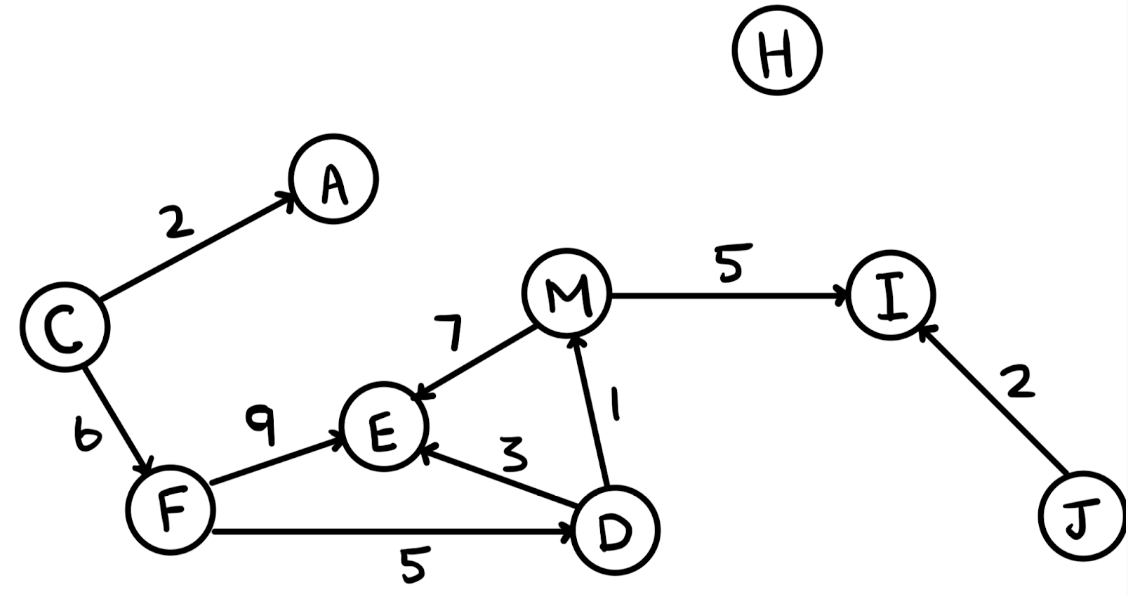
[17.6] Consider the following function and graph. What will be printed after the given function is called with the graph above?

def mystery(g):
   w = -1
   e1 = None
   e2 = None
   for node in g:
       for edge in g[node]:
           if edge[1] % 3 == 0:
               if edge[1] > w:
                   w = edge[1]
                   e1 = node
                   e2 = edge[0])
   print(w, e1, e2)
   

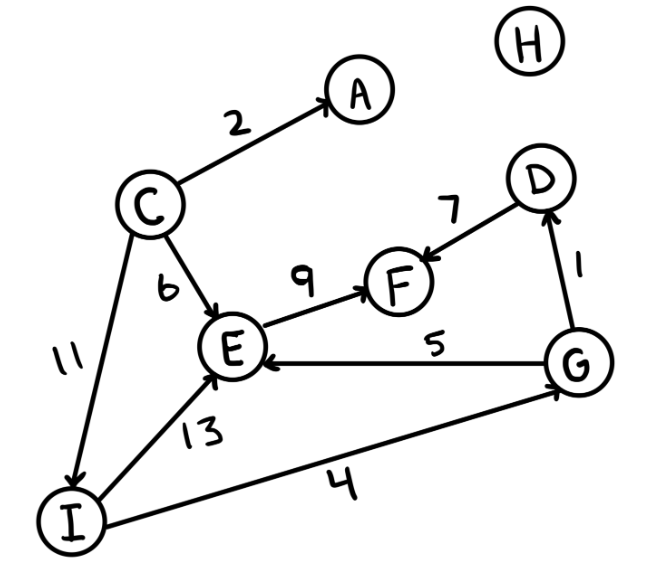
[17.7] Describe in words what this mystery function does:

def mystery2(g):
   total = 0
   for node in g:
       if node < "f":
           for edge in g[node]:
               if edge[0] < "f" and edge[1] % 2 != 0:
                   total += edge[1]
   return total
   

[17.8] Convert this Python representation of a graph into a drawing.

graph = {
   "a": ["b", "c"],
   "b": ["d", "e"],
   "c": ["d", "f"],
   "d": ["e", "f"],
   "e": ["f"],
   "f": ["a", "b"]
}

[17.9] Convert this graph to a Python representation.

g = { 
"A": [["C", 2]],  
"C": [["A", 2], ["E", 6]], 
"D": [["F", 7], ["G", 1], ["I", 5]], 
"E": [["C", 6], ["F", 9], ["G", 5]], 
"F": [["E", 9], ["D", 7], ["G", 3]],
"G": [["E", 5], ["F", 3], ["D", 1]],
"H": [],
"I": [["D", 5], ["J", 2]],
"J": [["I", 2]] 
}

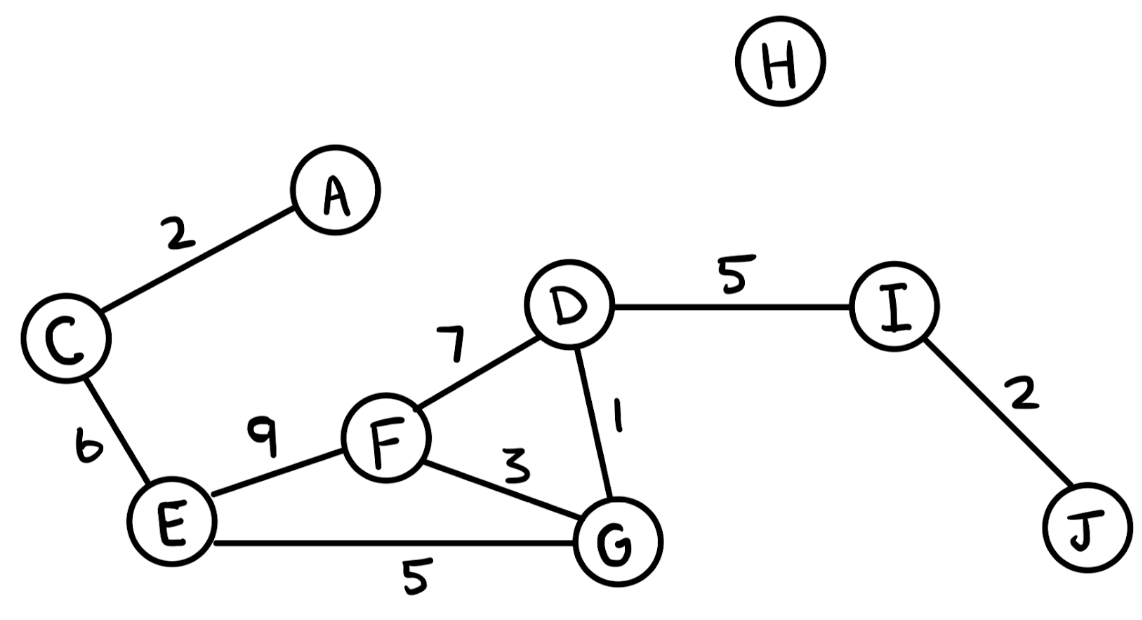
[17.10] Write a function getNodes(g) that returns the number of even valued nodes in a graph g. (Assume nodes are integer values).

def getNodes(g):
   evenNodes = 0
   # Loop through all nodes in the graph
   for node in g:
       # Check that the node is even
       if node % 2 == 0:
           evenNodes += 1
   return evenNodes

[17.11] Write a function getFriends(g) that takes in a graph representing a social network. Nodes correspond to people and each person has weighted edges to other people that are their friends. The edge weight corresponds to how good of friends they are. A weight of < 3 corresponds to these two people being best friends. We want to return the number of people who have two or more best friends.

def getFriends(g):
   totalPeople = 0
   # Loop through each node in the graph
   for person in g:
       # Count the number of best friends that this person has
       bestFriendsCount = 0

       # Loop through each friend of this person
       for edge in g[person]:
           if edge[1] < 3:
               bestFriendsCount += 1

       # If the person has 2 or more best friends, add them to the totalPeople count
       if bestFriendsCount >= 2:
           totalPeople += 1

   return totalPeople

[17.12] The CDC wants to ensure that people are practicing social distancing, so they want to notify people who are closer than 6 feet apart that they should spread out. Write a function that takes a graph as shown below and prints the names of people who are not socially distanced. Given the graph below for example, the function should print the following:

g = { 
"Amy": [["Ben", 7], ["Cloe", 6]], 
"Ben": [["Amy", 7], ["Cloe", 9], ["Denny", 7], ["Era", 3]], 
"Cloe": [["Amy", 6], ["Ben", 9], ["Denny", 4]], 
"Denny": [["Cloe", 4], ["Denny", 7]], 
"Era": [["Ben", 3]]
}

# prints:
# Ben Era
# Cloe Denny
# Denny Cloe
# Era Ben

    

def tooClose(g):
   # Loop through each node in the graph
   for node in g:
       # Loop through each edge of the current node
       for edge in g[node]:
           # If the edge is less than 6, add the node to the tooClose list and break out of the loop
           if edge[1] < 6:
               print(node, edge[0])

[17.13] Write a function to generate a list of all the nodes on a given graph (an example of such graph is shown below)

graph ={
    "a" : ["c"], 
    "b" : ["c", "e"], 
    "c" : ["a", "b", "d", "e"], 
    "d" : ["c"], 
    "e" : ["c", "b"], 
    "f" : []
}

print(listNodes(graph) # returns and prints ['a', 'b', 'c', 'd', 'e', 'f']

graph ={
    "a" : ["c"], 
    "b" : ["c", "e"], 
    "c" : ["a", "b", "d", "e"], 
    "d" : ["c"], 
    "e" : ["c", "b"], 
    "f" : []
}

def listNodes(g):
    r = []
    for node in g:
        r.append(node)
    return r
        

print(listNodes(graph))

[17.14] Write a function to find a given node's neighbors when the graph is unweighted. How would you change the function to find the node's neighbors for a weighted graph?

weighted = {
    "A" : [ ["B", 5], ["E", 2] ],
    "B" : [ ["A", 5], ["C", 3] ],
    "C" : [ ["B", 3], ["F", 9] ],
    "D" : [ ["E", 1], ["F", 7] ],
    "E" : [ ["A", 2], ["D", 1], ["F", 2] ],
    "F" : [ ["C", 9], ["D", 7], ["E", 2] ]
}

unweighted ={
    "a" : ["c"], 
    "b" : ["c", "e"], 
    "c" : ["a", "b", "d", "e"], 
    "d" : ["c"], 
    "e" : ["c", "b"], 
    "f" : []
}

def getNeighborsUnWeighted(g, node): 
    return g[node]


def getNeighborsWeighted(g, node): 
    neighbors = [ ] 
    for pair in g[node]: 
        neighbors.append(pair[0]) 
    return neighbors
        

[17.15] Write a function that takes a weighted graphs and returns the sum of all the weights

weighted = {
    "A" : [ ["B", 5], ["E", 2] ],
    "B" : [ ["A", 5], ["C", 3] ],
    "C" : [ ["B", 3], ["F", 9] ],
    "D" : [ ["E", 1], ["F", 7] ],
    "E" : [ ["A", 2], ["D", 1], ["F", 2] ],
    "F" : [ ["C", 9], ["D", 7], ["E", 2] ]
}

def sumEdges(g): 
    sumE = 0
    for node in g:
        for pair in g[node]: 
            sumE = sumE + pair[1]
    return sumE
        

[17.16] Write a function that prints all the edges in a given graph that is unweighted. How would the function change if the graph was weighted?

weighted = {
    "A" : [ ["B", 5], ["E", 2] ],
    "B" : [ ["A", 5], ["C", 3] ],
    "C" : [ ["B", 3], ["F", 9] ],
    "D" : [ ["E", 1], ["F", 7] ],
    "E" : [ ["A", 2], ["D", 1], ["F", 2] ],
    "F" : [ ["C", 9], ["D", 7], ["E", 2] ]
}

unweighted ={
    "a" : ["c"], 
    "b" : ["c", "e"], 
    "c" : ["a", "b", "d", "e"], 
    "d" : ["c"], 
    "e" : ["c", "b"], 
    "f" : []
}

def printEdgesUnWeighted(g): 
    for node in g: 
        for neighbor in g[node]: 
            print(node + "-" + neighbor)

def printEdgesWeighted(g): 
    for node in g: 
        for neighbor in g[node]: 
            print(node + "-" + neighbor[0])
        

[17.17] Write a function nameToFriends(g) that takes a social network as a graph and returns a new graph where the keys are the names of people in the network, and the value is the number of friends for that person.

g = { "Jon" : [ "Arya", "Tyrion" ],
      "Tyrion" : [ "Jaime", "Pod", "Jon" ],
      "Arya" : [ "Jon" ],
      "Jaime" : [ "Tyrion", "Brienne" ],
      "Brienne" : [ "Jaime", "Pod" ],
      "Pod" : [ "Tyrion", "Brienne", "Jaime" ],
      "Ramsay" : [ ]
    }

# Example call
nameToFriends(g) # returns {'Jon': 2, 'Tyrion': 3, 'Arya': 1, 'Jaime': 2, 'Brienne': 2, 'Pod': 3, 'Ramsay': 0}

def nameToFriends(g): 
    d = {}

    for person in g: 
        d[person] = len(g[person])
    return d
        

[17.18] Write a function popular(g) that takes a social network as a graph and returns the person in the network who has the most friends.

g = { "Jon" : [ "Arya", "Tyrion" ],
      "Tyrion" : [ "Jaime", "Pod", "Jon" ],
      "Arya" : [ "Jon" ],
      "Jaime" : [ "Tyrion", "Brienne" ],
      "Brienne" : [ "Jaime", "Pod" ],
      "Pod" : [ "Tyrion", "Brienne", "Jaime" ],
      "Ramsay" : [ ]
    }

def findMostPopular(g): 
    biggestCount = 0 
    mostPopular = None 

    for person in g: 
        if len(g[person]) > biggestCount: 
            biggestCount = len(g[person]) 
            mostPopular = person 
    return mostPopular
        

[17.19] Aperson wants to make more friends, so they're holding a party. They want to invite their own friends, but also anyone who is a friend of one of their friends. Write the function invite(g, person) that invites the given person's friends and the friends of their friends.

g = { "Jon" : [ "Arya", "Tyrion" ],
      "Tyrion" : [ "Jaime", "Pod", "Jon" ],
      "Arya" : [ "Jon" ],
      "Jaime" : [ "Tyrion", "Brienne" ],
      "Brienne" : [ "Jaime", "Pod" ],
      "Pod" : [ "Tyrion", "Brienne", "Jaime" ],
      "Ramsay" : [ ]
    }

def makeInviteList(g, person): 
    # start with immediate friends 
    invite = g[person] + [ ] # break alias 

    for friend in g[person]: 
        # find friends-of-friends 
        for theirFriend in g[friend]: 
            if theirFriend not in invite and theirFriend != person: 
                invite.append(theirFriend) 
    return invite
        

[17.20] Given an unweighted graph of a social network and two nodes (people) in the graph, return a list of the friends that those two people have in common. Write the function friendsInCommon(g, p1, p2). For example, in the graph shown below, calling friendsInCommon on "Jon" and "Jaime" would return the list [ "Tyrion" ].

g = { "Jon" : [ "Arya", "Tyrion" ],
      "Tyrion" : [ "Jaime", "Pod", "Jon" ],
      "Arya" : [ "Jon" ],
      "Jaime" : [ "Tyrion", "Brienne" ],
      "Brienne" : [ "Jaime", "Pod" ],
      "Pod" : [ "Tyrion", "Brienne", "Jaime" ],
      "Ramsay" : [ ]
    }

def friendsInCommon(g, p1, p2): 
    common = [] 

    for friend in g[p1]: 
       if friend in g[p2]:
           common.append(friend)
    return common