CMU 15-112 Summer 2020: Fundamentals of Programming and Computer Science
Homework 5 (Due Thu 28-May, at 5pm)

---

• This assignment is SOLO. This means you may not look at other student's code or let other students look at your code for these problems. See the syllabus for details.


• To start:
  1. Create a folder named 'hw5'
  2. Download hw5.py and cs112_m20_unit5_linter.py to that folder
  3. Edit hw5.py using VSCode
  4. When you are ready, submit hw5.py to Autolab. For this hw, you may submit up to 10 times, which is fewer times than you've had in the past but only your last submission counts.
• Do not use sets, dictionaries, or recursion in this assignment.
• Do not hardcode the test cases in your solutions.
• NOTE: We are not providing any test functions in this homework. That means that you need to write complete test functions for isLegalSudoku or getValidChessMoves (and all their helper functions).
• NOTE: This homework is going to be graded for style. Make sure that you adhere to the style guide when you're working on this HW, and double check your file against the style guide before you submit to Autolab!

---

A note about week 2 spiciness tracks
This week's mild and spicy problems will each follow a "track". In the mild track you will write isLegalSudoku, drawSudokuBoard, and playSudoku (a fully interactive sudoku game!). In the spicy track you will write getValidChessMoves, drawChessBoard, and playSimplifiedChess. Each day's homework assignment will require functions for the previous day's, so choosing a spiciness level for today locks you in for the week.

1. isLegalSudoku(board) [50 pts - Medium]
   This problem involves the game Sudoku, though we will generalize it to the N²xN² case, where N is a positive integer (and not just the 3²x3² case which is most commonly played). First, read the top part (up to History) of the Wikipedia page on Sudoku so we can agree on the rules. As for terminology, we will refer to each of the N² different N-by-N sub-regions as "blocks". The following figure shows each of the 4 blocks in a 2²x2² completed puzzle highlighted in a different color: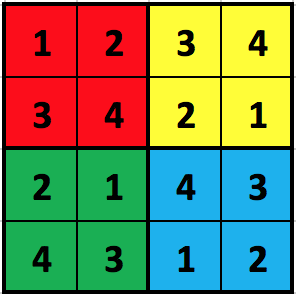
   
   
   While the next example shows the blocks of a 3²x3² incomplete puzzle: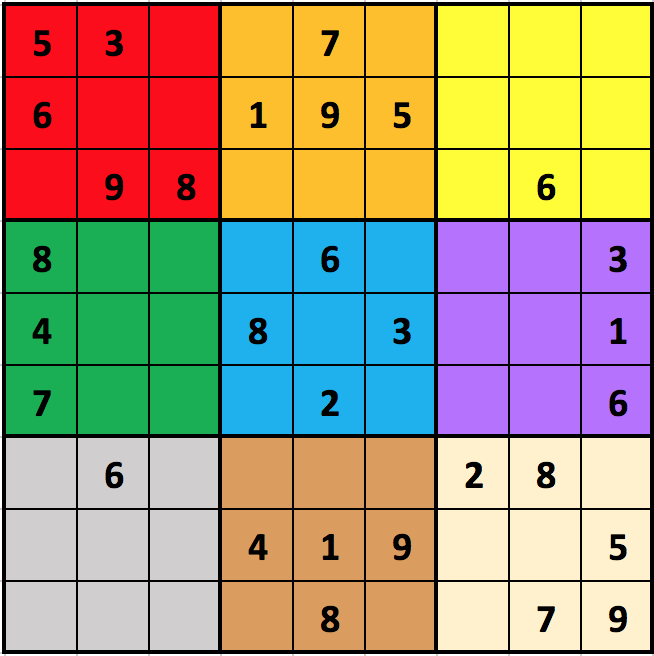
   
   
   For our purposes, we will number the blocks from 0 to N²-1 (hence, 0 to 8 in the figure), with block 0 in the top-left (red), moving across and then down (so, in the figure, block 1 is orange, block 2 is yellow, block 3 is green, block 4 is blue, block 5 is purple, block 6 is gray, block 7 is brown, and block 8 is tan). We will refer to the top row as row 0, the bottom row as row (N²-1), the left column as column 0, and the right column as column (N²-1).
   
   A Sudoku is in a legal state if all N⁴ cells are either blank (0) or contain a single integer from 1 to N² (inclusive), and if each integer from 1 to N² occurs at most once in each row, each column, and each block. A Sudoku is solved if it is in a legal state and contains no blanks.
   
   We will represent a Sudoku board as an N²xN² 2d list of integers, where 0 indicates that a given cell is blank. For example, here is how we would represent the 3²x3² Sudoku board in the figure above:

   [
     [ 5, 3, 0, 0, 7, 0, 0, 0, 0 ],
     [ 6, 0, 0, 1, 9, 5, 0, 0, 0 ],
     [ 0, 9, 8, 0, 0, 0, 0, 6, 0 ],
     [ 8, 0, 0, 0, 6, 0, 0, 0, 3 ],
     [ 4, 0, 0, 8, 0, 3, 0, 0, 1 ],
     [ 7, 0, 0, 0, 2, 0, 0, 0, 6 ],
     [ 0, 6, 0, 0, 0, 0, 2, 8, 0 ],
     [ 0, 0, 0, 4, 1, 9, 0, 0, 5 ],
     [ 0, 0, 0, 0, 8, 0, 0, 7, 9 ]
   ]
   

   With this description in mind, your task is to write some functions to indicate if a given Sudoku board is legal. To make this problem more approachable, we are providing a specific design for you to follow. And to make the problem more gradeable, we are requiring that you follow the design! So you should solve the problem by writing the following functions in the order given:
   
   
   1. areLegalValues(values) [0 pts (complete on collab5)]
      This function takes a 1d list of values, which you should verify is of length N² for some positive integer N and contains only integers in the range 0 to N² (inclusive). These values may be extracted from any given row, column, or block in a Sudoku board (and, in fact, that is exactly what the next few functions will do -- they will each call this helper function). The function returns True if the values are legal: that is, if every value is an integer between 0 and N², inclusive, and if each integer from 1 to N² occurs at most once in the given list (0 may be repeated, of course). Note that this function does not take a 2d Sudoku board, but only a 1d list of values that presumably have been extracted from some Sudoku board. Also, note that this function must be non-destructive.
   
   
   2. isLegalRow(board, row) [12.5 pts]
      This function takes a Sudoku board and a row number. The function returns True if the given row in the given board is legal (where row 0 is the top row and row (N²-1) is the bottom row), and False otherwise. To do this, your function must create a 1d list of length N² holding the values from the given row, and then provide these values to the areLegalValues function you previously wrote. (Actually, because areLegalValues is non-destructive, you do not have to copy the row; you may use an alias.)
   
   
   3. isLegalCol(board, col) [12.5 pts]
      This function works just like the isLegalRow function, only for columns, where column 0 is the leftmost column and column (N²-1) is the rightmost column. Similarly to isLegalRow, this function must create a 1d list of length N² holding the values from the given column, and then provide these values to the areLegalValues function you previously wrote.
   
   
   4. isLegalBlock(board, block) [15 pts]
      This function works just like the isLegalRow function, only for blocks, where block 0 is the left-top block, and block numbers proceed across and then down, as described earlier. Similarly to isLegalRow and isLegalCol, this function must create a 1d list of length N² holding the values from the given block, and then provide these values to the areLegalValues function you previously wrote.
   
   
   5. isLegalSudoku(board) [10 pts]
      This function takes a Sudoku board (which you may assume is a N²xN² 2d list of integers), and returns True if the board is legal, as described above. To do this, your function must call isLegalRow over every row, isLegalCol over every column, and isLegalBlock over every block. See how helpful those helper functions are?


2. getValidChessMoves(board, startRow, startcol) [50 pts - Spicy]
   First, carefully read about Simplified Chess here. We will use these rules, but for this assignment we will ignore pawn promotion.
   We will represent our chess board as a 2d list of spaces and unicode chess piece characters. So we would represent the starting board in Simplified Chess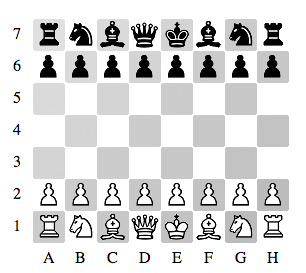
   
   like this:
   
   

   [
       ['♜','♞','♝','♛','♚','♝','♞','♜'],
       ['♟','♟','♟','♟','♟','♟','♟','♟'],
       [' ',' ',' ',' ',' ',' ',' ',' '],
       [' ',' ',' ',' ',' ',' ',' ',' '],
       [' ',' ',' ',' ',' ',' ',' ',' '],
       ['♙','♙','♙','♙','♙','♙','♙','♙'],
       ['♖','♘','♗','♕','♔','♗','♘','♖']
   ]
   

   
   With these descriptions in mind, your task is to write the function getValidChessMoves(board, startRow, startCol) which returns a list of the valid (row, col) positions that the piece at (startRow, startCol) can move to. For example, if we assume starterBoard is set to the Simplified Chess starter board above, getValidChessMoves(starterBoard, 0, 1) returns [(2,0), (2,2)] since these are the knight's valid moves. To make this problem more gradeable, we require that you write the following helper functions as part of your overall solution.
   
   
   1. getValidRookMoves(board, startRow, startCol) [8 pts]
   2. getValidBishopMoves(board, startRow, startCol) [8 pts]
   3. getValidQueenMoves(board, startRow, startCol) [5 pts]
   4. getValidKnightMoves(board, startRow, startCol) [8 pts]
   5. getValidPawnMoves(board, startRow, startCol) [8 pts]
   6. getValidKingMoves(board, startRow, startCol) [8 pts]
   7. getValidChessMoves(board, startRow, startCol) [5 pts]
   
   Though not required, we also found it helpful to write the function getPieceInfo(piece) which takes in a character like '♖' and returns a type/color tuple like ('rook', 'white').
   
   With this as a starting point, you'll be able to write an interactive game of chess in a few days! The first step is to know which moves the player is allowed to make.
   
   
   
   
   
   
3. CT Practice [20pts - Required]
   
   • To Start:
     1. Download unit5-ct-runner.py
     2. Log in with the username and password you received from us.
   • For full credit, you must complete a CT problem in under 5 minutes.
   • For every minute it takes you to complete the problem over 5 minutes you will lose 20% of the score for that problem.
   • You have unlimited attempts to complete each type of problem in the time limit and only your best score is counted.
   • Important: To receive any credit, you must quickly upload a picture of your scrap work and your submission confirmation to this form after getting a correct answer.
   • Your picture should show:
     1. Your box and arrow diagram
     2. Your Andrew ID
     3. The results table, including the correct answer, your answer, and the message "You answered correctly."