CMU 15-112: Fundamentals of Programming and Computer Science
Class Notes: Efficiency

1. Big-Oh
2. Common Function Families
3. Efficiency
4. The Big Idea
5. Examples
   1. Sequences, Nesting, and Composition
      
   2. A Few Sample Functions
      

1. Big-Oh
   1. Describes asymptotic behavior of a function
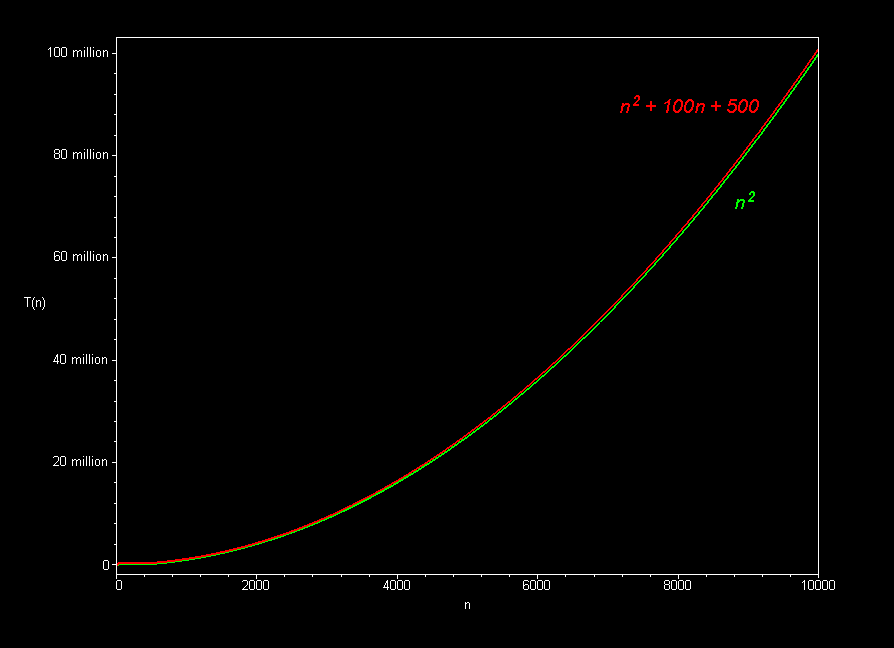
   2. Informally (for 15112): ignore all lower-order terms and constants
   3. Formally (after 15112): see here
   4. A few examples:
      • 3n² - 2n + 25 is O(n²)
      • 30000n² + 2n - 25 is O(n²)
      • 0.00000000001n² + 123456789n is O(n²)
      • 10nlog₁₇n + 25n - 17 is O(nlogn)


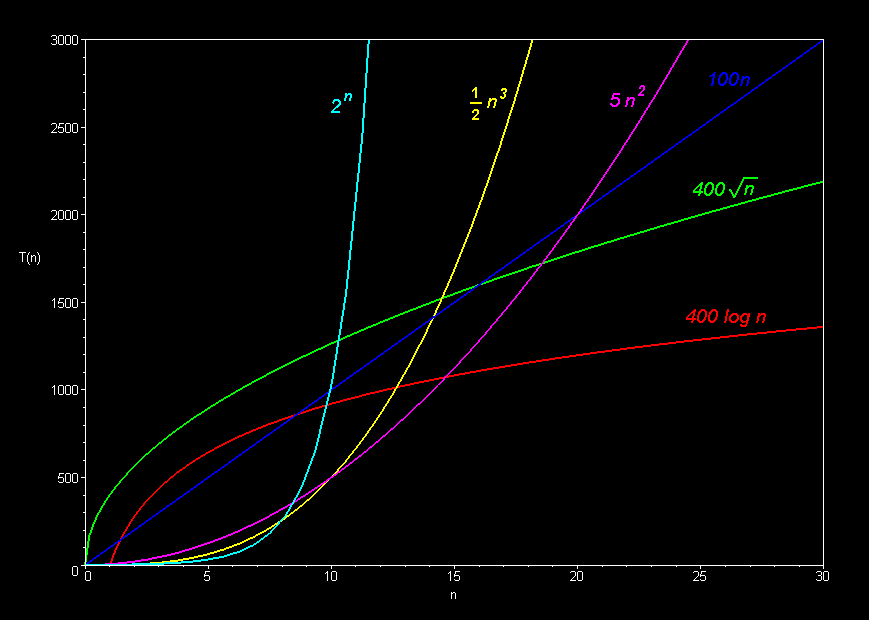
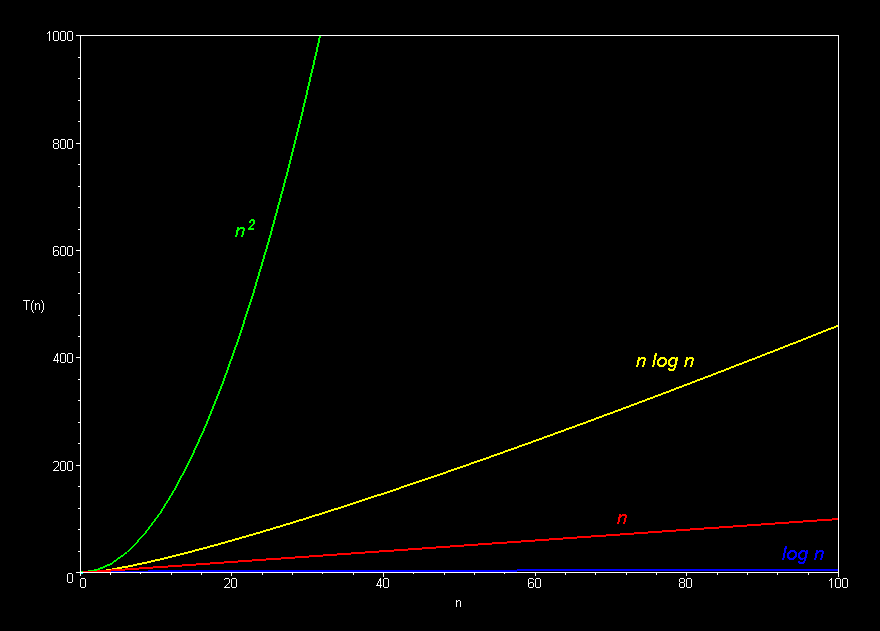
2. Common Function Families
   1. Constant O(1)
   2. Logarithmic O(logn)
   3. Square-Root O(n^0.5)
   4. Linear O(n)
   5. Linearithmic, Loglinear, or quasilinear O(nlogn)
   6. Quadratic O(n²)
   7. Exponential O(kⁿ)

Graphically (Images borrowed from here):







3. Efficiency
   When we say the program runs in O(f(N)), we mean...
   • N is the size of our input
     • For a string s, N = len(s)
     • For a list L, N = len(L) (also true for sets, dictionaries, and other collections)
     • For an integer n, N = numberOfDigits(n) = log_b(n), so n = b^N (where b is the base, and you can use any base b >= 2).
     • In the literature, N is often written in lowercase n, but we use that often to represent an integer n, which is different from the size of that integer. So in 112, we use uppercase N for the size of the input.
   • f(N) = resource consumption of our program
     • Resource can be time, space, bandwidth, ...
     • For 15112, we mainly care about time
   • For time, we usually measure algorithmic steps rather than elapsed time (These share the same big-oh, but algorithmic steps are easier to precisely describe and reason over)
   • Note that you can measure worst-case or average case, or even other cases such as best case (which often is trivial to compute and not very useful in practice). For 15-112, we often omit this term (which is a notable simplification that you will not see in future courses), and we nearly always mean worst-case, which is quite useful and generally easier to compute than average-case.
     • Count steps in a written algorithm, or comparisons and swaps in a list, etc
     • Can verify by timing your code's execution with: time.time()


4. The Big Idea
   • Each function family grows much faster than the one before it!
   • And: on modern computers, any function family is usually efficient enough on small n, so we only care about large n
   • So... Constants do not matter nearly as much as function families
   • Practically...
     • Do not prematurely or overly optimize your code
     • Instead: think algorithmically!!!


5. Examples
   1. Sequences, Nesting, and Composition
      • Sequencing
        
        # what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L.sort() # This is O(NlogN) L.sort(reverse=True) # This is O(NlogN) L[0] -= 5 # This is O(1) print(L.count(L[0]) + sum(L)) # This is O(N) + O(N)
      
      
      • Nesting
        
        # what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N for c in L: # This loop's body is executed O(N) times L[0] += c # This is O(1) L.sort() # This is O(NlogN) print(L) # This is O(N) (why?)
      
      
      • Composition
        
        # what is the total cost here? def f(L): # assume L is an arbitrary list of length N L1 = sorted(L) # This is O(NlogN) return L1 # This is O(1) def g(L): # assume L is an arbitrary list of length N L1 = L * len(L) # This is O(N**2) (why?) return L1 # This is O(1) L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L = f(g(L)) # What is the big-oh of this? print(L) # This is O(N**2) (why?)
   2. A Few Sample Functions
      • O(n)
        
        package main import "fmt" func findMax(a []int) int { max := a[0] for _, elem := range a { if elem > max { max = elem } } return max } func main() { fmt.Println(findMax([]int{1,8,6,4,9,7})) }
      
      
      • O(n^2)
        
        def getHighestCount(a): champElem = a[0] champCount = a.count(a[0]) for elem in a: count = a.count(elem) if count > champCount: champElem = elem champCount = count return champElem, champCount def main(): print(getHighestCount([1,2,2,3,4,5])) print(getHighestCount([1,2,1,1,3])) main()
      
      
      • O(log(n))
        
        package main import "fmt" func digitCount(n int) int { count := 0 for n > 0 { count += 1 n /= 10 } return count } func main() { fmt.Println(digitCount(15112)) }