CMU 15-112: Fundamentals of Programming and Computer Science
Class Notes: Efficiency

  1. Big-O
  2. Common Function Families
  3. Efficiency
  4. The Big Idea
  5. Examples
    1. Sequences, Nesting, and Composition
    2. Python Builtins
    3. sumOfSquares Examples
  1. Big-O
    1. Describes behavior of a function as the size of its input grows
    2. Informally (for 15112): ignore all lower-order terms and constants
    3. Formally (after 15112): see here
    4. A few examples in math functions:
      • 3n2 - 2n + 25 is O(n2)
      • 30000n2 + 2n - 25 is O(n2)
      • 0.00000000001n2 + 123456789n is O(n2)
      • 10nlog17n + 25n - 17 is O(nlogn)

  2. Common Function Families
    1. Constant O(1)
    2. Logarithmic O(logn)
    3. Square-Root O(n0.5)
    4. Linear O(n)
    5. Linearithmic, Loglinear, or quasilinear O(nlogn)
    6. Quadratic O(n2)
    7. Exponential O(kn)

    3. Graphically (Images borrowed from here):






  3. Efficiency
    When we say the program runs in O(N), we mean...
    • N is the size of our input
      • For a string s, N = len(s)
      • For a list lst, N = len(lst) (also true for sets, dictionaries, and other collections)
      • For an integer n, N = n
    • We can technically calculate Big-O for a number of program attributes, like time, space, bandwidth, etc. But in this class, we mainly care about time.
    • For time, we usually measure algorithmic steps rather than elapsed time (These share the same Big-O, but algorithmic steps are easier to precisely describe and reason over)
      • Algorithmic steps could be single lines of computation, or comparisons and swaps in a list, etc
      • Can verify by timing your code's execution with: time.time()
    • Note that you can measure worst-case or average case, or even other cases such as best case (which often is trivial to compute and not very useful in practice). For 15-112, we often omit this term (which is a notable simplification that you will not see in future courses), and we nearly always mean worst-case, which is quite useful and generally easier to compute than average-case.

  4. The Big Idea
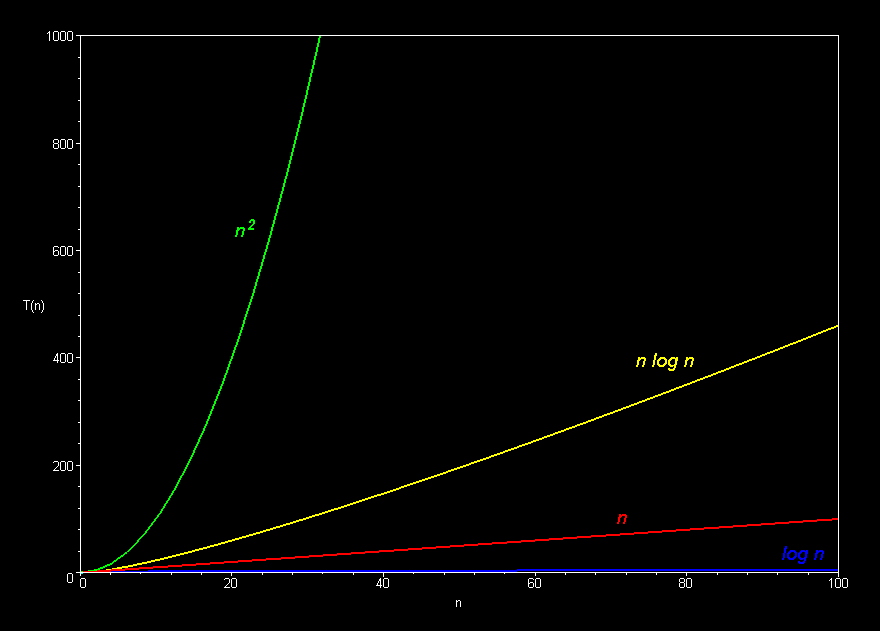
    • Each function family grows much faster than the one before it!
    • And: on modern computers, any function family is usually efficient enough on small n, so we only care about large n
    • So... Constants do not matter nearly as much as function families
    • Practically...
      • Do not prematurely or overly optimize your code
      • Instead: think algorithmically!!!

  5. Examples
    1. Sequences, Nesting, and Composition
      • Sequencing
        # what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L.sort() # This is O(NlogN) L.sort(reverse=True) # This is O(NlogN) L[0] -= 5 # This is O(1) print(L.count(L[0]) + sum(L)) # This is O(N) + O(N)

      • Nesting
        # what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N for c in L: # This loop's body is executed O(N) times L[0] += c # This is O(1) L.sort() # This is O(NlogN) print(L) # This is O(N) (why?)

      • Composition
        # what is the total cost here? def f(L): # assume L is an arbitrary list of length N L1 = sorted(L) # This is O(NlogN) return L1 # This is O(1) def g(L): # assume L is an arbitrary list of length N L1 = L * len(L) # This is O(N**2) (why?) return L1 # This is O(1) L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L = f(g(L)) # What is the Big-O of this? print(L) # This is O(N**2) (why?)

    2. Python Builtins
      The efficiency of the built-in functions in Python will affect the efficiency of the functions they are used in. We do not expect you to memorize the builtin efficiencies; instead, you should reason through why they have the efficiencies that they do.

      General
      Function/Method Complexity Code Example
      Print O(N) 
      # where N is the size of the input
print(input)
      Range in Iteration Number of iterations = (end - start)/step 
      for i in range(start, end, step):...
      Strings: s is a string with N characters
      Function/Method Complexity Code Example
      Len O(1) 
      len(s)
      Membership O(N) 
      "a" in s
      Get single character O(1) 
      value = s[index]
      Get slice O(end - start) 
      s[start:end]
      Get slice with step O((end - start)/step) 
      s[start:end:step]
      Chr() and Ord() O(1) 
      chr(s)
ord(s)
      Concatentation O(len(s1) + len(s2)) 
      s3 = s1 + s2
      Character Type Methods O(N) 
      s.isalnum()
s.isalpha()
s.isdigit()
s.islower()
s.isspace()
s.isupper()
      String Edit Methods O(N) 
      s.lower()
s.upper()
s.replace()
s.strip()
      Substring Search Methods O(N) 
      s.count()
s.startswith()
s.endswith()
s.find()
s.index()
      Lists: L is a list with N elements
      Function/Method Complexity Code Example
      Len O(1) 
      len(L)
      Append O(1) 
      L.append(value)
      Extend O(K) 
      # len(a) = K
L.extend(a)
      Concatentation with += O(K) 
      # len(a) = K
L += a
      Concatentation with + O(N + K) 
      # len(a) = K
L = L + a
      Membership Check O(N) 
      item in L
      Pop Last Value O(1) 
      L.pop()
      Pop Intermediate Value O(N) 
      L.pop(index)
      Count values in list O(N) 
      L.count(item)
      Insert O(N) 
      L.insert(index, value)
      Get value O(1) 
      value = L[index]
      Set value O(1) 
      L[index] = value
      Remove O(N) 
      L.remove(value)
      Get slice O(end - start) 
      L[start:end]
      Get slice with step O((end - start)/step) 
      L[start:end:step]
      Sort O(N log (N)) 
      L.sort()
sorted(L)
      Multiply O(N*D) 
      #where D is an int
A = L*D
      Minimum O(N) 
      min(L)
      Maximum O(N) 
      max(L)
      Copy O(N) 
      copy.copy(L)
      Deep Copy O(N*M) 
      # where L is a 2D list with N rows and M cols
copy.deepcopy(L)
      Sets: s is a set with N elements
      Function/Method Complexity Code Example
      Len O(1) 
      len(s)
      Membership O(1) 
      elem in s
      Adding an Element O(1) 
      s.add(elem)
      Removing an Element O(1) 
      s.remove(elem)
s.discard(elem)
      Union O(len(s) + len(t)) 
      s|t
      Intersection O(min(len(s), len(t))) 
      s&t
      Difference O(len(s)) 
      s - t
      Clear O(len(s)) 
      s.clear()
      Copy O(len(s)) 
      s.copy()
      Dictionaries: d is a dictionary with N key-value pairs
      Function/Method Complexity Code Example
      Len O(1) 
      len(d)
      Membership O(1) 
      key in d
      Get Item O(1) 
      value = d[key]
d.get(key, defaultValue)
      Set Item O(1) 
      d[key] = value
      Delete Item O(1) 
      del d[key]
      Clear O(N) 
      d.clear()
      Copy O(N) 
      d.copy()

      For a more complete list, see here

    3. sumOfSquares Examples
      Note: Run this code in Standard Python, as it will timeout if you run it in brython.
      # The following functions all solve the same problem: # Given a non-negative integer n, return True if n is the sum # of the squares of two non-negative integers, and False otherwise. def f1(n): for x in range(n+1): for y in range(n+1): if (x**2 + y**2 == n): return True return False def f2(n): for x in range(n+1): for y in range(x,n+1): if (x**2 + y**2 == n): return True return False def f3(n): xmax = int(n**0.5) for x in range(xmax+1): for y in range(x,n+1): if (x**2 + y**2 == n): return True return False def f4(n): xyMax = int(n**0.5) for x in range(xyMax+1): for y in range(x,xyMax+1): if (x**2 + y**2 == n): return True return False def f5(n): xyMax = int(n**0.5) for x in range(xyMax+1): y = int((n - x**2)**0.5) if (x**2 + y**2 == n): return True return False def testFunctionsMatch(maxToCheck): # first, verify that all 5 functions work the same print("Verifying that all functions work the same...") for n in range(maxToCheck): assert(f1(n) == f2(n) == f3(n) == f4(n) == f5(n)) print("All functions match up to n =", maxToCheck) testFunctionsMatch(100) # use larger number to be more confident import time def timeFnCall(f, n): # call f(n) and return time in ms # Actually, since one call may require less than 1 ms, # we'll keep calling until we get at least 1 secs, # then divide by # of calls we had to make calls = 0 start = end = time.time() while (end - start < 1): f(n) calls += 1 end = time.time() return float(end - start)/calls*1000 #(convert to ms) def timeFnCalls(n): print("***************") for f in [f1, f2, f3, f4, f5]: print ("%s(%d) takes %8.3f milliseconds" % (f.__name__, n, timeFnCall(f, n))) timeFnCalls(1001) # use larger number, say 3000, to get more accurate timing