Part One: Linear processing of a list
[1 point] Searching
In the file first_even.py, define a Python function first_even(numbers) that takes a list of integers (which might be empty) as a parameter. It should return the index of the first number in the list that is even. Caution: return the index, not the value in the list at that index! If no element of the list is even, return None. We don't care what your function does if its input is not a list of integers (that is, it's allowed to crash if the input is not a list of integers.)
When testing your program, be aware that if you call the function while in interactive mode with Python (e.g. in idle3 shell OR by using python3 -i in the terminal), and it returns the value None, normally you won't see that value displayed, unless you pass it to the print function.
Try it and see:
>>> def silly(): ... return None ... >>> silly() >>> print(silly()) None >>>
Example of first_even:
>>> from first_even import * (OR bash-3.2$ python3 -i first_even.py)
>>> first_even(list(range(5)))
0
>>> first_even([1, 3, 1, 5, 7, 9, 11, 13, 0])
8
>>> first_even([1, 3, 1, 5, 7, 9, 11, 13, 0, 11, 4])
8
>>> first_even([-5, 5, -1, 1, -4, 4])
4
>>> first_even([0])
0
>>> first_even([4,4])
0
>>> first_even([])
>>> first_even([1,1,1,1])
[1 point] Counting.
In the file num_even.py, define a Python function num_even(numbers) that takes a list of integers (which might be empty) as a parameter. It should return the number of elements of the input list that are even. We don't care what your function does if its input is not a list of integers (that is, it's allowed to crash.)
Example:
>>> from num_even import * (OR bash-3.2$ python3 -i num_even.py) >>> num_even([]) 0 >>> num_even(list(range(10))) 5 >>> num_even([-1]*10) 0 >>> num_even([0]*10) 10 >>> num_even([-6, -4, -2, 0, 2, 4, 6, 99]) 7 >>> num_even([99, -6, -4, -2, 0, 2, 4, 6]) 7 >>>
[2 points] Geometric Mean
In mathematics, the geometric mean is one of several kinds of averages. The geometric mean of a list of \(n\) positive numbers \(x_0, x_1, \dots x_{n-1}\) (\(n\) must be at least 1) is equal to
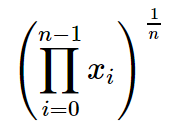
This is the same as
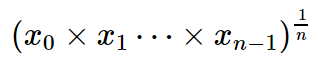
In the file geo_mean.py define the function geo_mean(numbers) that takes a non-empty list of positive numbers (integers or floating point numbers) called numbers and returns the geometric mean of these numbers. Again, we don't care what your function does if its input is not a non-empty list of positive numbers (that is, it's allowed to crash.)
Example:
>>> from geo_mean import * (OR bash-3.2$ python3 -i geo_mean.py) >>> geo_mean([9]) 9.0 >>> geo_mean([2, 8]) 4.0 >>> geo_mean([.5, 32]) 4.0 >>> geo_mean([1/32, 1, 4]) 0.5 >>>
[2 points] Remembering state during linear processing
In second_largest.py, define a function second_largest(values) that takes a list containing at least two items as input and returns the second largest item in the list. In the case that the largest item occurs more than once, it would then be considered both the largest and second largest item. For example, the list [1, 3, 2, 3] has 3 as the largest and second largest item. You may assume that there are at least two items in the list and that the items in the list are all the same type, that is, all numbers or all strings or all Booleans; if not, we don't care what your function does.
You must have an iterative solution (i.e. a loop) for this problem in order to receive credit.
Here are some hints on how to write this function. First, try to write a working function that finds the largest item in a list. The approach to take to this easier problem is to initialize a variable largest to the very first item. Then use a loop to compare each subsequent item to largest, and change the value of largest if need be. When all the items have been examined, you can be sure that largest is indeed the largest item, and you can return it. Once you have this function working, you can modify it and use a similar approach to find the second largest item by keeping track of both the largest and the second largest items (you'll need two variables for this). Then return the second largest item instead of the largest one. Be careful to initialize these two variables properly: think how your function should behave if there are only two items in the list. Also take care with the loop bounds; to find the second largest instead of the largest item the loop bounds should be different.
In Python, you can use the max and min functions to find, respectively, the maximum and the minimum of two values of the same type.
Example:
>>> max(True, False)
True
>>> min(-4, -1)
-4
>>> min('a', 'b')
'a'
>>> from second_largest import * (OR >>> quit()
bash-3.2$ python3 -i second_smallest.py)
>>> second_largest([3, -2, 10, -1, 5])
5
>>> second_largest([-2, 1, 1, -3, 5])
1
>>> second_largest([1,1,3,3])
3
>>> second_largest(["alpha", "gamma", "beta", "delta"])
'delta'
>>> second_largest([3.1, 3.1])
3.1
>>> second_largest([False, True, False, False])
False
>>> second_largest([True, False, True])
True
>>>
Part Two: Sorting
Another sorting algorithm
There are many different sorting algorithms, adapted to different purposes. If all the items in the list to be sorted come from a small, finite set of values (maybe they are all integers between 0 and 10000, for instance), then a linear-time algorithm known as counting sort can be used. (This algorithm is the basis of a family of fast special-purpose algorithms, including radix sort, used for punched cards.) For this problem, you will implement counting sort for a list of integers, and verify by experiment that it is a linear-time algorithm.
Here is a description of the algorithm. The input is a list of non-negative integers keys and another integer max_key that tells us the maximum key that could occur in the list.
- Initialize a list called counts to have a length of max_key + 1 and contents of all zeroes.
- For each key in keys, increment counts[key] by 1.
- Initialize an empty list called result.
- For each key from 0 to max_key inclusive, append counts[key] copies of key to result.
- return result
What is the running time of this algorithm? We can see that there are two loops: one to examine each element of the list to be sorted, and one to examine the list of counts. Call the length of the list to be sorted n. The list of counts must have max_key + 1 elements. Therefore, if the operations within these loops can be done in constant time, the time complexity of the algorithm must be linear in the larger of n and max_key + 1.
You will implement this algorithm as a function (described below), write another function that measures the time taken by the sorting function, and use that to check that your sorting algorithm indeed runs in time linear in the size of its input.
[2 points] Implementing the algorithm: implement the algorithm given above as a function counting_sort(keys, max_key). The parameters are the list of keys (all nonnegative integers) and the maximum possible key. Again, if the input doesn't obey these rules, we don't care what the function does. The function should not alter its input list; it should return another list containing the values sorted into increasing order.
In order to initialize all the counts to zero, the easiest thing to do is to use the * (asterisk) operator for lists, which works as shown here:
>>> n = 5 >>> my_list = [0] * n >>> my_list [0, 0, 0, 0, 0] >>>
For step IV, it's easiest to use the extend method for lists, which works as shown here:
>>> my_list = [] >>> other_list = [10, 10, 10, 10] >>> my_list.extend(other_list) >>> my_list [10, 10, 10, 10] >>> another_list = [50, 60] >>> my_list.extend(another_list) >>> my_list [10, 10, 10, 10, 50, 60] >>>
Sorting example:
>>> counting_sort([44, 22, 44, 11, 33, 33, 22, 44, 33, 44], 44) [11, 22, 22, 33, 33, 33, 44, 44, 44, 44] >>> counting_sort([], 0) [] >>> counting_sort([5], 5) [5] >>> counting_sort([5, 5, 5, 5], 5) [5, 5, 5, 5] >>> counting_sort(list(range(10)), 9) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] >>> counting_sort(list(range(9, -1, -1)), 9) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[1 point] Measuring time: write another function time_sort(n) to measure and return the approximate time taken by counting sort. The input n indicates the size of the list to be sorted. Your function should create a list of the integers from 0 to n-1 (this is easy using list(range(n))) and call the counting sort function to sort the list. Never mind that it's already sorted; the function will work the same way anyway.
How do we measure the time taken? First, before your function definition, include the following line:
from time import time
Within the function definition for time_sort, after creating the list to be sorted, but before calling counting_sort, incude the following:
start = time()This sets the variable start to the current time. Then, after calling counting_sort, return the value time() - start. By subtracting start from the current time after counting_sort is done, this finds the elapsed time in seconds of the sort.
Note that there's no test function supplied for time_sort(). It's your responsibility to make sure it behaves reasonably. For example, try choosing a large enough n so that sorting takes about 5 seconds by the clock, and make sure that the value returned is more than about 2 and less than 5 (it will be less than clock time, because creating the list to be sorted takes significant time when n is large.)
[1 point] Checking that the time complexity is linear: Now you can check that your implementation of counting sort has linear time complexity. You will not get credit for part a unless the complexity is linear. There is no code to write, but you should hand in a file containing a transcript of your interaction with Python, showing that as you double the value of n, the time reported by time_sort approximately doubles. You will need to find appropriate values of n so that the times are not too short to do a meaningful comparison. Look for values that produce times in the neighborhood of a few hundredths of a second to between one and two seconds. Include at least five data points. You can create the transcript by cutting and pasting from the shell window to a text file. Call the file time_transcript.txt. Here's an example of how it should look (your numbers won't be exactlly the same as these):
>>> from counting_sort import * (OR bash-3.2$ python3 -i counting_sort.py) >>> time_sort(100000) 0.06032991409301758 >>> time_sort(200000) 0.11398506164550781 >>> time_sort(400000) 0.21988797187805176 >>> time_sort(800000) 0.43526506423950195 >>> time_sort(1600000) 0.8658199310302734