- f1 = A ∧ (B ∨ C)
-
f2 = ¬ A ∨ (¬ B ∧ ¬ C)
- What kind of a relationship do you observe about the formulae f1 and f2 by looking at their truth tables, in particular, at columns for A, B, C, f1, and f2?
Hint: Remember how we create truth tables. We systematically list all possible combinations of the truth values for the variables in the Boolean formula, and the truth values of expressions involving these variables. For example, for Part a, all you need to do is to fill in the table below.
A B C (B ∨ C) A ∧ (B ∨ C) -------------- ------- ------------ 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
The commutative rule lets us switch the order of two terms, while the associative rule lets us move parentheses around (or add or remove them) when the connectives are all the same. The above table shows that step 2 was derived from step 1 via the commutative rule, step 3 was derived from step 2 via the associative rule, and step 4 was derived from step 3 via the idempotence rule. We can also use DeMorgan's Law to transform expressions (as in lecture). Here is the proof that ¬ (A ∧ (B ∨ C)) is equivalent to ¬ A ∨ (¬ B ∧ ¬ C):
Step Formula Justification (Rule) 1. A ∧ (B ∧ A) Commutative 2. A ∧ (A ∧ B) Associative 3. (A ∧ A) ∧ B Idempotence 4. A ∧ B
Step Formula Justification (Rule) 1. ¬ (A ∧ (B ∨ C)) DeMorgan's Law 2. ¬ A ∨ ¬ (B ∨ C) DeMorgan's Law 3. ¬ A ∨ (¬ B ∧ ¬ C)
- How can you explain your answer to 1.c. in terms of De Morgan's Law? Hint: See the derivation above.
- The formula f1 from Problem 1 represents a Boolean function. Draw the combinational circuit that can compute f1 using AND, OR and NOT gates.
- Draw a combinational circuit that computes the equivalent of the Boolean function f2 that uses a single AND, a single OR and a single NOT gate.
- How could you realize the expression ¬ (A ∧ ¬ (B ∧ C)) using only NAND gates and no other type of gate?
A seven-segment display can be used to form each of the ten decimal digits as shown below.
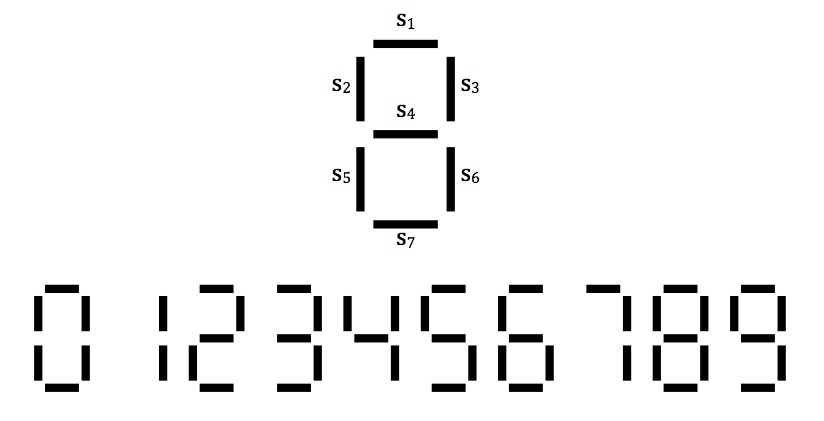
We can define a circuit abstractly below that requires four Boolean inputs A, B, C, and D, and produces seven Boolean outputs s1, s2, ..., s7 to make the segments of the display form digits:
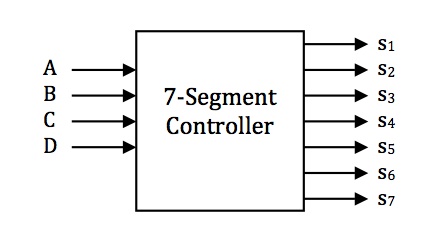
A segment si is lit if si is 1 (True) and not lit if si is 0 (False).
-
Derive a Boolean formula for s7 that is
True (1) if and only if segment s7 is lit.
Your answer should be of the following form:
s7 = (________) ∨ (________) ∨ (________) ∨ ...
where each missing section is a Boolean expression with all 4 input variables that is True when ABCD represents a decimal digit that results in the segment s7 of the display being lit. To help you get started, the digit 0 (binary 0000) will light segment s7, so the first expression in the formula above would be
(¬A ∧ ¬B ∧ ¬C ∧ ¬D)
since s7 would be True (i.e. 1) if A = 0, B = 0, C = 0, and D = 0. You will need to find all of the other missing expressions for s7. Hint: Consider all the digits for which s7 would be lit.
- Derive a simple Boolean expression for s6 that is True (i.e. 1) if and only if the segment s6 is lit. (HINT: Segment s6 is lit for all digits except when the digit is the number 2.)
- A
word size is characteristic to a given computer architecture. It denotes the number of digits that a CPU can process at one time. Modern processors, usually have a word size of 8, 16, 24, 32 or 64 bits; most current general purpose computers use 32 or 64 bits. The word size of a modern computer typically also describes the size of the address space on that computer. For example, a computer that is said to be "32-bit" usually allows 32-bit memory addresses.What is the largest amount of memory in gigabytes that can be directly addressable in a 32-bit architecture? Assume that the archicture supports byte-addressable memory where each addressable location corresponds to one byte of memory.
- What does it mean for a programming language to be high-level? In answering this question you may use external resources. However, your answer should be given in your own words and any references you use should be cited.