[4 points]
Recall that a binary tree is a non-linear data structure where each node has at most two children, which we call left child
and right child. For example, here is a binary tree with three nodes where we call 4 (the parent), 1 (left child)
and 5 (right child).

Binary trees are defined recursively where left child of a node can be another binary tree as shown below. In the binary tree below, left child
of node with value 4 is subtree that contains the nodes, 0, 1 and 2.

Implementation: In most languages trees are implemented using "pointers".
The concept of pointers is beyond the scope of this course. However, we can view a binary tree as a list as shown below
Tree = [left_child, key, right_child]
where left_child and right_child are binary trees themselves.
We define an empty tree as a tree equals to nil. Lets take a look at the following binary tree
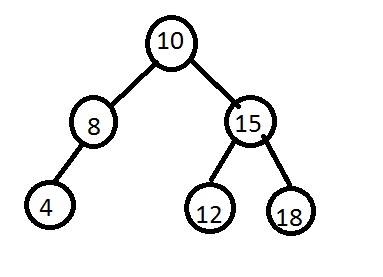
the above tree can be represented as a list (of lists) as follows.
Tree = [[[nil, 4, nil], 8, nil], 10, [[nil,12,nil],15,[nil,18,nil]]]
[1 points] Our first attempt is to define a function is_binary_tree(tree) (in
basic.rb) that, when passed a tree,
will return TRUE if tree is an array representing a binary tree.
A binary tree is represented as a list of length 3 (tree[0]=left_child, tree[1]=key, tree[2]=right_child)
To check whether it is a binary tree, we check if tree is an array of length three and this must be checked recursively for all sublists.
If the list is not a binary tree, then return FALSE. Lets call this the binary tree invariant. That is, the condition that is is
represented as a list of size 3 must be true
for the entire tree including all subtrees. Here is the recursive algorithm that checks
if the tree (and all its nested subtrees) satisfy the requirement of three element lists (and sublists)
-
if the tree is nil return true (An empty tree is a binary tree).
Check if the list representing the tree has three elements (we use tree.length to check this)
Recursively check if the left_child of the tree is a binary tree itself
Recursively check if the right_child of the tree is a binary tree itself
Assignment: For this part, type the following code into a ruby file basic.rb and test with sample inputs shown
Recent changes in Red
#A helper function to check if a is an array
def is_array(a)
a.class == Array
end
#A helper function that also checks for empty array
def is_any_array(a)
return (a==nil or is_array(a))
end
#Check if the tree is a binary tree
def is_binary_tree(t)
if (t==nil)
return true #empty tree is a tree
end
if (is_any_array(t) == false) #tree must be represented as an array
return false
end
if (t.length==3 and t[1]!=nil) #length of the array must be 3 for it to be a binary tree
return (is_any_array(t[0]) == true and #make sure left child is an array
is_any_array(t[2]) == true and #make sure right child is an array
is_binary_tree(t[0]) and #make sure left child is a binary tree(recursive)
is_binary_tree(t[2])) #make sure right child is a binary tree(recursive)
else
return false
end
end
Testing the code (expected output shown)
>> t = nil >> is_binary_tree(t) => true >> t = [nil, 2, 3] >> is_binary_tree(t) => false >> t = [nil, 3, nil] >> is_binary_tree(t) => true >> t = [[nil,2,nil], 3, nil] >> is_binary_tree(t) => true >> t = [[nil,2,nil], 3, [nil,1,2]] >> is_binary_tree(t) => false
[1 point] Define a function build_tree_node(key) (in
basic.rb) that, when passed the value of a key,
will return a valid binary tree node. In this case, you are expected to build a list of three elements
with key as t[1]. You leave t[0] (left_child)
and t[2] (right_child) as nil. You may assume that key is a
an integer.)
Assignment: For this part, write the code for build_tree_node(key) in the
ruby file basic.rb and test with sample inputs shown
Testing the code (expected output shown)
>> key = 3 >> t = build_tree_node(key) >> is_binary_tree(t) => true >> key = 1 >> t = build_tree_node(key) >> is_binary_tree(t) => trueUse few other inputs to test the functions
[1 point] Define a function get_key_value(tree) (in
basic.rb) that, when passed a tree,
will return the value of the key. You must return nil if the tree is nil or not a binary tree
(use is_binary_tree above to test if the tree is a binary tree)
Assignment: For this part, write the code for get_key_value(tree) in the
ruby file basic.rb and test with sample inputs shown
Testing the code (expected output shown)
>> t=nil >> get_key_value(t) => nil >> t=build_tree_node(3) >> get_key_value(t) => 3 >> t=[nil,4,nil] >> get_key_value(t) => 4 >> t=[[nil,2,nil],3,nil] >> get_key_value(t) => 3 >> t=[nil,5,[nil,2,nil]] >> get_key_value(t) => 5 >> t=[3,5,[nil,2,nil]] >> get_key_value(t) => nilUse few other inputs to test the functions
[1 points] Define a function insert_left_if_nil(tree,key) (in
basic.rb) that, when passed a tree and a key value,
will return a tree that contains a left_child whose key value is key. If the tree is not a
binary tree or is empty tree then return nil.If the left_child of the tree is not nil then return nil.
Assignment: For this part, write the code for insert_left_if_nil(tree,key) in the
ruby file basic.rb and test with sample inputs shown
Testing the code (expected output shown)
>> t=nil >> insert_left_if_nil(t,3) => nil >> t=[nil,2,3] >> insert_left_if_nil(t,2) => nil >> t=[[nil,2,nil],2,nil] >> insert_left_if_nil(t,1) => nil >> t=[nil,2,nil] >> insert_left_if_nil(t,3) => [[nil,3,nil],2,nil] >> t=[nil,2,[nil,4,nil]] >> insert_left_if_nil(t,1) => [[nil,1,nil],2,[nil,4,nil]] >> t=[nil,2,[nil,4,3]] >> insert_left_if_nil(t,1) => nilUse few other inputs to test the functions
[6 points] Binary tree is a non-linear data structure that is inherently recursive. That is, a tree is defined as
tree = [left_child, key, right_child] where left_child and right_child are binary trees themselves.
In this part we will use recursion to implement some advanced operations on trees.
Consider an example function insert_as_left_most_leaf(tree,key). The function inserts key as the left
most leaf node of the binary tree. A node is a leaf node if its left_child and
right_child are both nil. For example, [nil, 3, nil] represents a leaf node with key value 3.
The function insert_as_left_most_leaf is a powerful recursive function. We use recursion to
go down the left branch of the tree until we can find the left most node. Then we insert the key as the left
child of the current left most node. If the tree is not a binary tree then return nil.
If the tree is empty, then the new node becomes the tree. If the
left child of the tree is empty, then new key becomes the left node. Otherwise we recursively go down the
tree until we can find the left most node with an empty left child.
def insert_as_left_most_leaf(tree,key)
if is_binary_tree(tree)==false
return nil
end
if tree==nil
return [nil,key,nil] #if tree is empty, then the tree is the new node
end
if tree[0]==nil #if the left child of the tree is empty, then
tree[0]=[nil,key,nil] #create a new node and insert as the new left node
return tree
else
return [insert_as_left_most_leaf(tree[0],key),tree[1],tree[2]] #recursively go down the tree on left child (tree[0]) until you find a empty place
end
end
Convince your self that the function works. How do we do that? You can try to trace this code on a piece of
paper. Try different trees and key values to see how the recursion actually works.
(OPTIONAL) Here is a video clip that can help you understand recursion, writing code and tracing it.
Assignment: First, type the code given above for insert_as_left_most_leaf in the ruby file operations.rb and test with sample inputs shown
Testing the code (expected output shown)
>> t=nil >> insert_as_left_most_leaf(t,3) => [nil,3,nil] >> t=[nil,3,[nil,4,nil]] >> insert_as_left_most_leaf(t,5) => [[nil,5,nil],3,[nil,4,nil]] >> t=[nil,3,4] >> insert_as_left_most_leaf(t,5) => nil >> t=[[nil,2,nil],3,[nil,4,nil]] >> insert_as_left_most_leaf(t,5) => [[[nil,5,nil],2,nil],3,[nil,4,nil]] >> t=[[[nil,1,nil],2,nil],3,[nil,4,nil]] >> insert_as_left_most_leaf(t,5) => [[[[nil,5,nil],1,nil],2,nil],3,[nil,4,nil]] Try with different inputs
-
[2 point] We can recursively define the total number of nodes (lets call this count) in a binary tree. That is, the total nodes is equal to 1 + count(left_subtree) + count(right_subtree) . Write the function count(tree) (in operations.rb) that implements counting nodes as a recursive function. You may want to write the algorithm first considering base cases (such as tree is empty) and then the recursive case. The code should not be more than a few lines. The logic for your recursive function is as follows.
The number of nodes in an empty tree is 0, otherwise it is 1 + count(left_subtree) + count(right_subtree). If the tree is not a binary tree, return nil.
Assignment: Write the function count in the ruby file operations.rb and test with sample inputs shown
Testing the code (expected output shown)
>> t=nil >> count(t) => 0 >> t=[nil,3,[nil,4,nil]] >> count(t) => 2 >> t=[nil,3,4] >> count(t) => nil >> t=[[nil,2,nil],3,[nil,4,nil]] >> count(t) => 3 >> t=[[[nil,1,nil],2,nil],3,[nil,4,nil]] >> count(t) => 4 Test your code with different inputs
-
[2 point] We can recursively find the height of a binary tree. The height of a binary tree is defined as the length of the longest path from root to a leaf node. A leaf node is a node, whose left and right children are nil. The length of a path is the total number of nodes in the path.
For example, lets take a look at the following tree. The tree has height 4 since we can count a maximum of 4 nodes from root(84) to a leaf node. In this case, there are multiple paths of length 4 ending with a leaf node (10,26,43,85,94)

Here is an algorithm to find the height of a binary tree.
-
if the tree is empty then the height is 0 .
Otherwise the height is 1 + max(height(left_subtree), height(right_subtree))
We note that a max function (as a helper or built in Ruby function) is necessary to implement the height function (recursively).
Assignment: Write the function height(tree) in the ruby file operations.rb and test with sample inputs as shown
Testing the code (expected output shown)
>> t=nil >> height(t) => 0 >> t=[nil,3,[nil,4,nil]] >> height(t) => 2 >> t=[nil,3,4] >> height(t) => nil >> t=[[nil,2,nil],3,[nil,4,nil]] >> height(t) => 2 >> t=[[[nil,1,nil],2,nil],3,[nil,4,nil]] >> height(t) => 3 Test your code with different inputs
[2 point] Using the function insert_as_left_most_leaf(tree,key) as a guide, write the function
insert_as_right_most_leaf(tree,key). The function insert_as_right_most_leaf is a powerful
recursive function.
We use recursion to
go down the right branch of the tree until we can find the right most node. Then we insert the key as the right
child of the current right most node. If the tree is not a binary tree then return nil.
If the tree is empty, then the new node becomes the tree. If the
right child of the tree is empty, then new key becomes the right node. Otherwise we recursively go down the
tree until we can find the right most node with an empty right child.
Assignment: Write the function insert_as_right_most_leaf in the
ruby file operations.rb and test with sample inputs shown
Testing the code (expected output shown)
>> t=nil >> insert_as_right_most_leaf(t,3) => [nil,3,nil] >> t=[nil,3,[nil,4,nil]] >> insert_as_right_most_leaf(t,5) => [nil,3,[nil,4,[nil,5,nil]]] >> t=[nil,3,4] >> insert_as_right_most_leaf(t,5) => nil >> t=[[nil,2,nil],3,[nil,4,nil]] >> insert_as_right_most_leaf(t,5) => [[nil,2,nil],3,[nil,4,[nil,5,nil]]] >> t=[[[nil,1,nil],2,nil],3,[nil,4,nil]] >> insert_as_right_most_leaf(t,5) => [[nil,1,nil],2,nil],3,[nil,4,[nil,5,nil]]] Test your code with different inputs
Submission
You should now have a pa6 directory, containing:
-
basic.rb
operations.rb
Zip up your directory and upload it using the autolab system. (The autolab system will accept submissions beginning on Monday until the deadline Thursday night.)