15110 Spring 2013 [Kaynar/Gunawardena]

Programming Assignment 7 - due Thursday, March 28

Note: You are responsible for protecting your solutions to these problems from being seen by other students either physically (e.g., by looking over your shoulder) or electronically. (More information can be found in the instructions for Programming Assignment 2.)

Style

Part I: Data Representation

For Part I of this assignment, you will create a Ruby source file containing a Ruby function(s) implementing each of the problems described below. In implementing these functions, you may not use to_s, to_i or any built-in Ruby function that converts between numbers and strings. You may, however, use subscripting with [ ] to convert a character in a string to its ASCII value and use chr to convert an integer to the corresponding character with that ASCII value.

1. [2 points] We can implement decimal to binary conversion in Ruby by using the following algorithm that takes a non-negative integer \(n\) as input and returns a string of 1's and 0's holding the binary representation of \(n\).

   1. If \(n\) is zero return "0"
   2. Let s be an empty string.
   3. While \(n > 0\) do the following:
      1. Let ch be "0" if \(n\) is even and "1" if \(n\) is odd.
      2. Add ch to the beginning of s.
      3. Divide \(n\) by 2 using integer division and set \(n\) to the quotient.
   4. Return s.

   Write a function int_to_bin_string(n) (in int_to_bin_string.rb) that implements the algorithm above.

   Example:

   >> int_to_bin_string(255)
   => "11111111"
   >> int_to_bin_string(1024)
   => "10000000000"
   >> int_to_bin_string(4)
   => "100"
   

2. [2 points] The value of a binary number represented as a string s can be found by iterating over the indices of the string and, for each index i, updating value to so it reflects the value of the substring represented by s[0..i]. An example is shown in the table below:

   s	i	s[i]	value
   "10101"	0	"1"	1
   "10101"	1	"0"	2 = 2*1 + 0
   "10101"	2	"1"	5 = 2*2 + 1
   "10101"	3	"0"	10 = 2*5 + 0
   "10101"	4	"1"	21 = 2*10 + 1

   Write a function bin_string_to_int(s) in bit_string_to_int.rb that takes a non-empty string of 1's and 0's and converts it into the corresponding integer value.

   Example:

   >> bin_string_to_int("0")
   => 0
   >> bin_string_to_int("1")
   => 1
   >> bin_string_to_int("101")
   => 5
   >> bin_string_to_int("0011101110")
   => 238
   

   Hint: Remember that if s is a string, s[0] is the ASCII value of the character at position 0 in s. If s is "Hello", then s[0] is not "H", it's 72, and s[0].chr is "H".

   Another hint: In the binary system, adding a digit \(k\) to the right of a given binary number \(n\) means multiplying \(n\) by 2 and adding \(k\) to the result. For example, the decimal value of the binary number 111₂ is 7. This can be obtained from the binary number 11₂ by multiplying the value of the binary number 11₂ by 2 and adding 1 to the result.

3. [1 points] Write a function hex_string_to_bin_string(hex_string) (in hex_string_to_bin_string.rb) that converts a non-empty string containing the hexadecimal representation of a number (using the characters "0"-"9" and "A"-"F" as digits) into a string containing that number's binary representation. You can assume that the function is always called with a well-formed hexadecimal number.

   Hint: A hexadecimal number can be converted to a binary number by converting each hexadecimal digit in order. For example, the hexadecimal number 9AF can be converted by converting 9, A, and F to binary strings and concatenating them in the given order.

   Example:

   >> hex_string_to_bin_string("4")
   => "0100"
   >> hex_string_to_bin_string("D")
   => "1101"
   >> hex_string_to_bin_string("4D")
   => "01001101"
   >> hex_string_to_bin_string("2DA")
   => "001011011010"
   

Part II: Boolean Logic and Gates

4. [1 point] In the file one_bit_full_adder.rb, write a Ruby function one_bit_full_adder(a,b,cin) that takes three Boolean values as input and prints the result of every gate in the full adder circuit below. Note that ^ is the Ruby exclusive or (xor) operator. If you do not recall this operator, and cannot recognize why it is relevant, you can visit page 12 of the slide deck "Boolean Logic" to see its truth table. Use && for logical and || for logical or; do not use the and and or keywords.

   
   

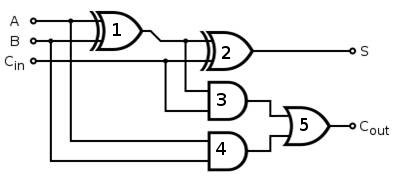
   Example output:

   >> one_bit_full_adder(true,false,true)
   XOR gate 1 outputs true
   XOR gate 2 (S) outputs false
   AND gate 3 outputs true
   AND gate 4 outputs false
   OR gate 5 (Cout) outputs true
   => nil
   

5. [3 points] Visit the lecture slides for Unit 8B and make sure that you understand the description of a full adder on slide 13. Now write your own Ruby function table_full_adder in file table_full_adder.rb to compute and print the truth table on that slide, using the formulas shown. Your code should use nested for loops. Hint: Notice that the carry out bit \(C_{out}\) and the sum bit \(S\) are computed from A, B, and the carry in bit \(C_{in}\). Think about what this implies for your loop structure.

Part III

[3 pts] For part III of this assignment, you will work on a module in the Online Learning Initiative at CMU that will teach you about a new topic called cellular automata. This module will help you learn the basics about cellular automata before we cover this topic in class next week. The module is designed so we can focus in class on the parts of the topic that you find more difficult, which in turn will hopefully maximize your learning for this topic.

In order to get credit for this part, you must complete the module by the deadline for the programming part. We will not be grading you on how many questions you get right in the module. Instead, we will be grading you on whether you completed the module on time or not.

To access the Cellular Automata module:

1. Go to this URL: http://oli.cmu.edu
   1. If you do not have an account, click on the "Register" link in the upper right. Click on the "CMU users sign in here" link.
   2. If you already have an account, Sign In: Click on the "CMU users sign in here" link.
2. Enter your course key 15110s13 into the box labeled "Register for a course" as shown at right.
3. Follow the instructions on the My Courses page to get started on the Cellular Automata module.
4. You don't have to do then entire module in one sitting; you can leave the web site and resume work on it later.

Submission

You should have a pa7 directory, containing:

1. int_to_bin_string.rb
2. bin_string_to_int.rb
3. hex_string_to_bin_string.rb
4. one_bit_full_adder.rb
5. table_full_adder.rb

Zip up your directory and upload it using the autolab system.