15-110 Spring 2013 [Gunawardena/Kaynar]

Problem Set 5 - due Friday, February 22 in class

Reading Assignment

Read sections 5.1-5.6 in chapter 5 of the textbook Explorations in Computing.

Instructions

Type or neatly write the answers to the following problems.
Please STAPLE your homework before you hand it in.
On the first page of your homework, include your name, andrew ID, lab section (A-N), and the assignment number.
You must hand in your homework at the start of class on the given due date.

Exercises

(1 pt) Write a recursive Ruby function sum(n) that has one parameter n that is a positive integer. Your function should return the sum of the integers from n down to 1. For example sum(4) returns 10 (that is 4+3+2+1) Your solution must use recursion and should not have a loop in it.
(1 pt) Write a recursive Ruby function print_triangle(n) that has one parameter n. The function will print an upside down triangle using a recursive function. Your solution must use recursion and should NOT have a loop in it. Hint:
For example, print_triangle(4) will print the following triangle
****
***
**
*

Hint: You may find the following print_stars function useful. You can include this function in your solution.
```
def print_stars(n)
   if (n==0) then
      print "\n"
   else
    print("*")
    print_stars(n-1)
   end
end
```
For example, print_stars(3) will print: ***
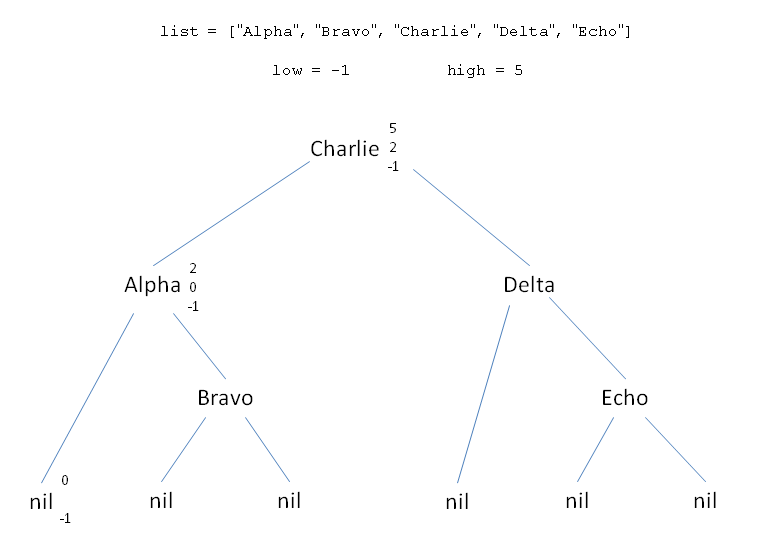
(4 pts) Do you believe that the binary search algorithm we studied works in all cases? What about edge cases, such as a key that precedes the first element in the list or follows the last element? What if the integer division (low+high)/2 causes problems when the list has an even number of elements, or an odd number of elements? Here is a repeat of the algorithm:
```
def binsearch(list, key)
  low = -1
  high = list.length
  while low+1 < high
    mid = (low+high) / 2
    if key == list[mid] then
      return mid
    elsif key < list[mid] then
      high = mid
    else
      low = mid
    end
  end
  return nil
end
```
One way to convince yourself that the algorithm works is to show that every possible position in the ordered list, including both the values themselves (when the key is found) and the positions between values (when the key is not found and the binary search should return nil), can be derived by following the algorithm for updating mid, low, and high. To do this, we're going to construct a complete binary search tree. First we introduce some notation for depicting nodes in the search tree:

X

high

mid

low

nil

high

low

The above nodes are generated by starting with the low and high values. If low+1 is less than high, then we compute mid, and compare the key against that element of the list, e.g., the string "X" as shown above. If they match we return mid, otherwise we take either the left or right branch. But if low+1 is equal to instead of less than high, then we stop and return nil, as in the node on the right.
(i) In the diagram below, we've filled in the numeric values for three of the nodes for the case where the key is "Aardvark". The binary search always begins with low = -1 and high = 5, giving mid = 2, which puts us at "Charlie". So all searches of this list start at "Charlie". If the key is less than this value, the algorithm tells us to set high equal to mid, so we have a high of 2 and a low of -1, which gives a mid of 0, taking us to node "Alpha", as shown. If we go left from "Alpha" (because the key is less than "Alpha"), the next node has a high of 0 and a low of -1. Since now low+1 = high, the algorithm returns nil, making this node a terminal (leaf) node. Print out the diagram, or redraw it yourself, and complete the tree by following the algorithm to fill in all the missing values, so that every node has either two or three numbers written next to it. For example, you might choose a key of "Bravo" and see how the algorithm gets to that node. Then choose a key of "Banana" and see at which leaf node the algorithm ends. And so on. Include your complete annotated tree in the pages you hand in.

(ii) Notice that all the terminal (leaf) nodes are nil. What pattern do you notice in the numbers attached to these nodes?
(iii) Notice that all the nonterminal (branch) nodes contain elements of the list. What pattern do you notice in their mid values?
(2 pts) Let's use the recursive, non-destructive version of the merge sort algorithm covered in lecture to sort the array [15, 25, 56, 11, 22, 27, 38, 43]:

Non-Destructive Merge Sort Algorithm:
Step 1. Sort the first half of the array using merge sort.
Step 2. Sort the second half of the array using merge sort.
Step 3. Merge the two sorted halves to get a sorted result array.
1. Show the value of newlist1 (first half of the array) after step 1 of the algorithm is completely done.
2. Show the value of newlist2 (second half of the array) after step 2 of the algorithm is completely done.
3. Show the merge process of step 3 by tracing this step as shown in the course slides/notes, giving the values for a_index, b_index, and c at each iteration.
4. Explain why this algorithm is recursive. What is its base case?
(2 pts) Quick sort is another algorithm for sorting data. In this version of the algorithm, we compare all of the elements in the list to the middle element (list[list.length/2]), which we will call the pivot. All of those that are less than the pivot go into one list and all of those that are greater than or equal to the pivot go into a second list. Then we sort these two sublists (recursively). The final sorted list is the first sorted sublist followed by the pivot followed by the second sorted sublist.
For example, if we want to sort the list
```
list = [56, 42, 82, 75, 18, 58, 27, 61, 84, 41, 21, 15, 71, 90, 33]
```
we create two lists, separating the elements based on the pivot 61 (the "middle" value of the list):
```
list1 = [56, 42, 18, 58, 27, 41, 21, 15, 33]
list2 = [82, 75, 84, 71, 90]
```
Each sublist is sorted recursively (final results shown for each sublist):
```
list1 = [15, 18, 21, 27, 33, 41, 42, 56, 58]
list2 = [71, 75, 82, 84, 90]
```
and list1 + {61} + list2 are combined to show the final result
```
[15, 18, 21, 27, 33, 41, 42, 56, 58] + [61] + [71, 75, 82, 84, 90]
=> [15, 18, 21, 27, 33, 41, 42, 56, 58, 61, 71, 75, 82, 84, 90]
```
Consider this quick sort algorithm sorting a list of n integers.
1. Into what two sublists would this algorithm split the list [56, 42, 18, 58, 27, 41, 21, 15, 33] ?
2. This algorithm is recursive. What is the base case for this recursion? (In other words, when does quick sort stop partitioning a list into two sublists?) BE CAREFUL: This is a little trickier than it seems.
3. The two sublists list1 and list2 need not be of the same length. One could even be empty. Construct an example list (of size 7 or less) that would assure that picking middle element always lead to two lists, list1 and list2 "almost" of equal size. This would assure the quicksort of an order of complexity of O(n log n). Give a simple example of a list and justify your answer.
4. Explain how an unlucky sequence of pivots could give this algorithm a worst case complexity of O(n²). Give a simple example of a list(size 7 or less) to justify your answer.