Class Notes: Efficiency

1. Big-Oh
2. Common Function Families
3. Efficiency
4. The Big Idea
5. Examples
   1. Python Builtins
      
   2. isPrime vs fasterIsPrime
      
6. Linear Search vs Binary Search
7. Sorting
8. Optional: sumOfSquares Examples
   

Big-Oh

  video
1. Describes asymptotic behavior of a function
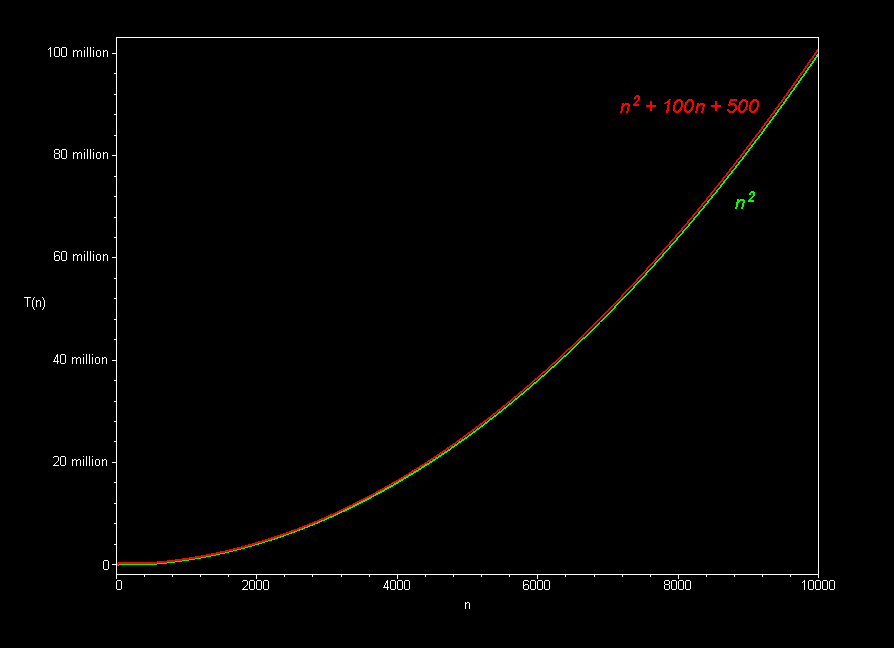
2. Informally (for 15112): ignore all lower-order terms and constants
3. Formally (after 15112): see here
4. A few examples:
   • 3n² - 2n + 25 is O(n²)
   • 30000n² + 2n - 25 is O(n²)
   • 0.00000000001n² + 123456789n is O(n²)
   • 10nlog₁₇n + 25n - 17 is O(nlogn)

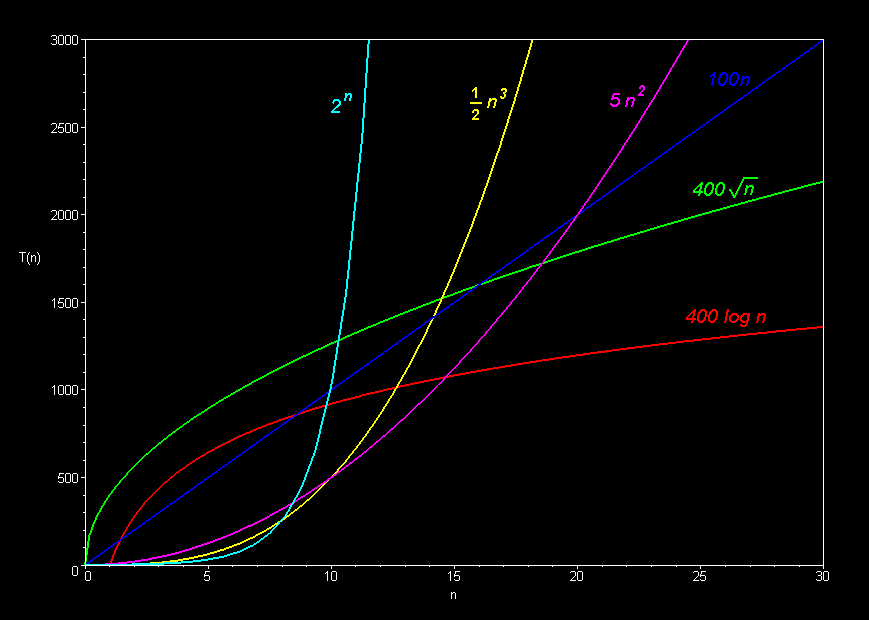
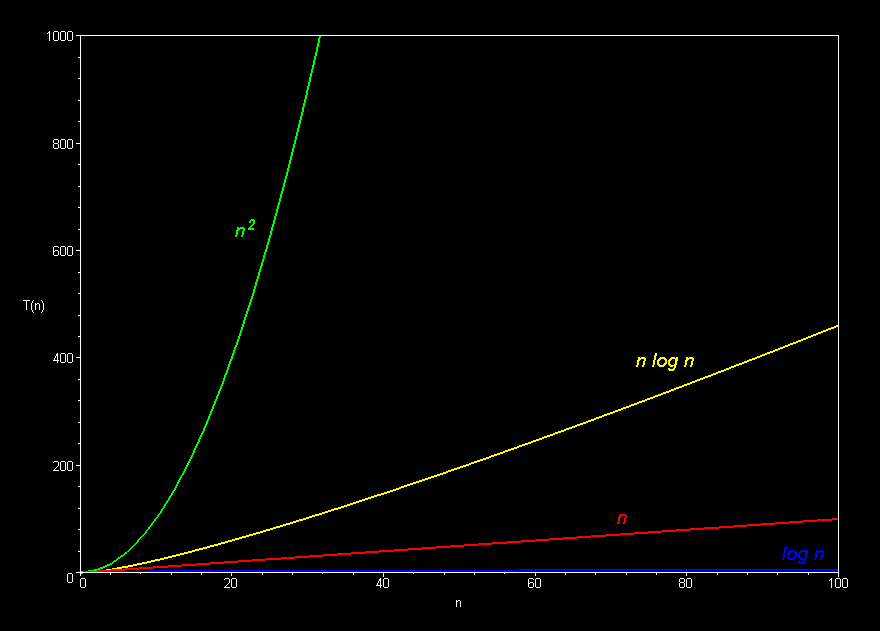
Common Function Families

  video
1. Constant O(1)
2. Logarithmic O(logn)
3. Square-Root O(n^0.5)
4. Linear O(n)
5. Linearithmic, Loglinear, or quasilinear O(nlogn)
6. Quadratic O(n²)
7. Exponential O(kⁿ)

Graphically (Images borrowed from here):







Efficiency

  video
When we say the program runs in O(f(N)), we mean...
• N is the size of our input
  • For a string s, N = len(s)
  • For a list L, N = len(L) (also true for sets, dictionaries, and other collections)
  • For an integer n, N = numberOfDigits(n) = log_b(n), so n = b^N (where b is the base, and you can use any base b >= 2).
  • In the literature, N is often written in lowercase n, but we use that often to represent an integer n, which is different from the size of that integer. So in 112, we use uppercase N for the size of the input.
• f(N) = resource consumption of our program
  • Resource can be time, space, bandwidth, ...
  • For 15112, we mainly care about time
• For time, we usually measure algorithmic steps rather than elapsed time (These share the same big-oh, but algorithmic steps are easier to precisely describe and reason over)
• Note that you can measure worst-case or average case, or even other cases such as best case (which often is trivial to compute and not very useful in practice). For 15-112, we often omit this term (which is a notable simplification that you will not see in future courses), and we nearly always mean worst-case, which is quite useful and generally easier to compute than average-case.
  • Count steps in a written algorithm, or comparisons and swaps in a list, etc
  • Can verify by timing your code's execution with: time.time()

The Big Idea

  video
• Each function family grows much faster than the one before it!
• And: on modern computers, any function family is usually efficient enough on small n, so we only care about large n
• So... Constants do not matter nearly as much as function families
• Practically...
  • Do not prematurely or overly optimize your code
  • Instead: think algorithmically!!!

Examples

Python Builtins

  video
Here we use S for a set and L for a list:
• Some are O(1), including len(L), (val in S), L.append(item)
• Some are O(N), including max(L), min(L), (val in L), L.count(val), set(L)
• Sorting is O(NlogN)
• Optional: For a more complete list, see here

isPrime vs fasterIsPrime

  video

• From here, isPrime tests O(n) values and fasterIsPrime tests only O(n^0.5) values.
• So fasterIsPrime is much faster.
• Considerably faster primality tests exist. For example, the AKS Primality Test.

Linear Search vs Binary Search

  video
• Linear search
  • Basic idea: check each element in turn
  • Use: find an element in an unsorted list
  • Cost: O(N)
• Binary search
  • Basic idea: in a sorted list, check middle element, eliminate half on each pass
  • Uses:
    • Find an element in a sorted list
    • Number-guessing game (eg: guess a random number between 1 and 1000)
    • Find a root (zero) of a function with bisection (adapted binary search)
  • Cost: O(logN)

Sorting

1. Sorting Algorithms
   There are dozens of common sorting algorithms. We will study these in particular:
   • Selection Sort: repeatedly select the smallest (or largest) remaining element and swap it into sorted position.
   • Merge Sort: sort blocks of 1's into 2's, 2's into 4's, etc, on each pass merging sorted blocks into sorted larger blocks.


2. Using the Sorting Simulator (xSortLab)
   Check out xSortLab for Selection Sort and Merge Sort. Be sure to understand the Visual Sort as well as the Timed Sort.


3. Sorting Code Examples and Timing
   

   # sorting.py
   
   import time, random
   
   ####################################################
   # swap
   ####################################################
   
   def swap(a, i, j):
       (a[i], a[j]) = (a[j], a[i])
   
   ####################################################
   # selectionSort
   ####################################################
   
   def selectionSort(a):
       n = len(a)
       for startIndex in range(n):
           minIndex = startIndex
           for i in range(startIndex+1, n):
               if (a[i] < a[minIndex]):
                   minIndex = i
           swap(a, startIndex, minIndex)
   
   ####################################################
   # mergeSort
   ####################################################
   
   def merge(a, start1, start2, end):
       index1 = start1
       index2 = start2
       length = end - start1
       aux = [None] * length
       for i in range(length):
           if ((index1 == start2) or
               ((index2 != end) and (a[index1] > a[index2]))):
               aux[i] = a[index2]
               index2 += 1
           else:
               aux[i] = a[index1]
               index1 += 1
       for i in range(start1, end):
           a[i] = aux[i - start1]
   
   def mergeSort(a):
       n = len(a)
       step = 1
       while (step < n):
           for start1 in range(0, n, 2*step):
               start2 = min(start1 + step, n)
               end = min(start1 + 2*step, n)
               merge(a, start1, start2, end)
           step *= 2
   
   ####################################################
   # builtinSort (wrapped as a function)
   ####################################################
   
   def builtinSort(a):
       a.sort()
   
   ####################################################
   # testSort
   ####################################################
   
   def testSort(sortFn, n):
       a = [random.randint(0,2**31) for i in range(n)]
       sortedA = sorted(a)
       startTime = time.time()
       sortFn(a)
       endTime = time.time()
       elapsedTime = endTime - startTime
       assert(a == sortedA)
       print(f'{sortFn.__name__:>20} n={n}, time={elapsedTime:6.3f}')
   
   
   def testSorts():
       n = 2**8 # use 2**8 for Brython, use 2**12 or larger for Python
       for sortFn in [selectionSort, mergeSort, builtinSort]:
           testSort(sortFn, n)
   
   testSorts()

   Select Visualize Run


4. Some Sorting Links
   
   • Wikipedia page on Sorting
   • Excellent sorting animation website
   • Sorting algorithm animation video (15 algorithms in 6 minutes)
   • Even more sorting algorithm animations


5. Sorting Analysis
   This is mostly informal, and all you need to know for a 112-level analysis of these algorithms. You can easily find much more detailed and rigorous proofs on the web.
   • selectionsort
     On the first pass, we need N compares and swaps (N-1 compares and 1 swap).
     On the second pass, we need only N-1 (since one value is already sorted).
     On the third pass, only N-2.
     So, total steps are about 1 + 2 + ... + (N-1) + N = N(N+1)/2 = O(N²).
   
   
   • mergesort
     On each pass, we need about 3N compares and copies (N compares, N copies down, N copies back).
     So total cost = (3N steps per pass) x (# of passes)
     After pass 0, we have sorted lists of size 2⁰ (1)
     After pass 1, we have sorted lists of size 2¹ (2)
     After pass 2, we have sorted lists of size 2² (4)
     After pass k, we have sorted lists of size 2^k
     So we need k passes, where N = 2^k
     So # of passes = k = log₂N
     Recall that total cost = (3N steps per pass) x (# of passes)
     So total cost = (3N)(log₂N) = O(NlogN).
     Note: This is the theoretical best-possible O() for comparison-based sorting!

Optional: sumOfSquares Examples


Note: this section is optional. Also: Run this code in Standard Python, as it will timeout if you run it in brython.

# The following functions all solve the same problem:
# Given a non-negative integer n, return True if n is the sum
# of the squares of two non-negative integers, and False otherwise.

def f1(n):
    for x in range(n+1):
        for y in range(n+1):
            if (x**2 + y**2 == n):
                return True
    return False

def f2(n):
    for x in range(n+1):
        for y in range(x,n+1):
            if (x**2 + y**2 == n):
                return True
    return False

def f3(n):
    xmax = int(n**0.5)
    for x in range(xmax+1):
        for y in range(x,n+1):
            if (x**2 + y**2 == n):
                return True
    return False

def f4(n):
    xyMax = int(n**0.5)
    for x in range(xyMax+1):
        for y in range(x,xyMax+1):
            if (x**2 + y**2 == n):
                return True
    return False

def f5(n):
    xyMax = int(n**0.5)
    for x in range(xyMax+1):
        y = int((n - x**2)**0.5)
        if (x**2 + y**2 == n):
            return True
    return False

def testFunctionsMatch(maxToCheck):
    # first, verify that all 5 functions work the same
    print("Verifying that all functions work the same...")
    for n in range(maxToCheck):
        assert(f1(n) == f2(n) == f3(n) == f4(n) == f5(n))
    print("All functions match up to n =", maxToCheck)

testFunctionsMatch(100) # use larger number to be more confident

import time
def timeFnCall(f, n):
    # call f(n) and return time in ms
    # Actually, since one call may require less than 1 ms,
    # we'll keep calling until we get at least 1 secs,
    # then divide by # of calls we had to make
    calls = 0
    start = end = time.time()
    while (end - start < 1):
        f(n)
        calls += 1
        end = time.time()
    return float(end - start)/calls*1000 #(convert to ms)

def timeFnCalls(n):
    print("***************")
    for f in [f1, f2, f3, f4, f5]:
        print(f'{f.__name__}({n}) takes {timeFnCall(f, n):8.3f} milliseconds')

timeFnCalls(1001)  # use larger number, say 3000, to get more accurate timing

Select