Class Notes: Recursion, Part 2
- File System Navigation (optional) Folders can contain folders or files. Since folders can contain other folders, they are a recursive data structure. In fact, they are a kind of recursive structure called a tree (where each value has exactly one parent, and there is a topmost or "root" value). Traversing such a recursive data structure is a natural use of a recursive algorithm!
- printFiles
- listFiles
- removeTempFiles
- Fractals
- sierpinskiTriangle
- Koch curve and Koch snowflake The Koch curve is a fractal that replaces a line segment with 4 connected line segments that are all 1/3 of the size of the original line.
- Backtracking
- maze solving Python code: maze-solver.py
- nQueens Python code: nQueens.py
- Memoization (optional)
- The problem:
def fib(n): if (n < 2): return 1 else: return fib(n-1) + fib(n-2) import time def testFib(maxN=40): for n in range(maxN+1): start = time.time() fibOfN = fib(n) ms = 1000*(time.time() - start) print(f'fib({n:2}) = {fibOfN:8}, time = {ms:5.2f}ms') testFib() # gets really slow!
- A solution:
fibResults = dict() def fib(n): if (n in fibResults): return fibResults[n] if (n < 2): result = 1 else: result = fib(n-1) + fib(n-2) fibResults[n] = result return result import time def testFib(maxN=40): for n in range(maxN+1): start = time.time() fibOfN = fib(n) ms = 1000*(time.time() - start) print(f'fib({n:2}) = {fibOfN:8}, time = {ms:5.2f}ms') testFib() # ahhh, much better!
- A more elegant solution:
def memoized(f): # You are not responsible for how this decorator works. You can just use it! import functools cachedResults = dict() @functools.wraps(f) def wrapper(*args): if args not in cachedResults: cachedResults[args] = f(*args) return cachedResults[args] return wrapper @memoized def fib(n): if (n < 2): return 1 else: return fib(n-1) + fib(n-2) import time def testFib(maxN=40): for n in range(maxN+1): start = time.time() fibOfN = fib(n) ms = 1000*(time.time() - start) print(f'fib({n:2}) = {fibOfN:8}, time = {ms:5.2f}ms') testFib() # ahhh, much better!
These programs only run locally (not in the browser), and require that you first download and expand sampleFiles.zip in the same folder as the Python file you are running.
import os
def printFiles(path):
# Base Case: a file. Just print the path name.
if os.path.isfile(path):
print(path)
else:
# Recursive Case: a folder. Iterate through its files and folders.
for filename in os.listdir(path):
printFiles(path + '/' + filename)
printFiles('sampleFiles')
# Note: if you see .DS_Store files in the sampleFiles folders, or in the
# output of your function (as often happens with Macs, in particular),
# don't worry: this is just a metadata file and can be safely ignored.
import os
def listFiles(path):
if os.path.isfile(path):
# Base Case: return a list of just this file
return [ path ]
else:
# Recursive Case: create a list of all the recursive results from
# all the folders and files in this folder
files = [ ]
for filename in os.listdir(path):
files += listFiles(path + '/' + filename)
return files
print(listFiles('sampleFiles'))
Note: Be careful when using os.remove(): it's permanent and cannot be undone!
That said, this can be handy, say to remove .DS_Store files on Macs, and can be modified to remove other kinds of files, too. Just be careful.
import os
def removeTempFiles(path, suffix='.DS_Store'):
if path.endswith(suffix):
print(f'Removing file: {path}')
os.remove(path)
elif os.path.isdir(path):
for filename in os.listdir(path):
removeTempFiles(path + '/' + filename, suffix)
removeTempFiles('sampleFiles')
# removeTempFiles('sampleFiles', '.txt') # be careful
A fractal is a recursive graphic (that is, a graphic that appears the same at different levels as you zoom into it, so it appears to be made of smaller versions of itself). In theory you can zoom forever into a fractal, but here we will keep things simple and draw fractals only up to a specified level. Our base case will be when we reach that level. We'll use the following framework for most fractals:
from cmu_112_graphics import *
def appStarted(app):
app.level = 1
def drawFractal(app, canvas, level, otherParams):
if level == 0:
pass # base case
else:
pass # recursive case; call drawFractal as needed with level-1
def keyPressed(app, event):
if event.key in ['Up', 'Right']:
app.level += 1
elif (event.key in ['Down', 'Left']) and (app.level > 0):
app.level -= 1
def redrawAll(app, canvas):
margin = min(app.width, app.height)//10
otherParams = None
drawFractal(app, canvas, app.level, otherParams)
canvas.create_text(app.width/2, 0,
text = f'Level {app.level} Fractal',
font = 'Arial ' + str(int(margin/3)) + ' bold',
anchor='n')
canvas.create_text(app.width/2, margin,
text = 'Use arrows to change level',
font = 'Arial ' + str(int(margin/4)),
anchor='s')
canvas.create_text(app.width/2, app.height/2,
text = 'Replace this with your fractal',
font = 'Arial 24 bold')
runApp(width=400, height=400)
from cmu_112_graphics import *
def appStarted(app):
app.level = 1
def drawSierpinskiTriangle(app, canvas, level, x, y, size):
# (x,y) is the lower-left corner of the triangle
# size is the length of a side
# Need a bit of trig to calculate the top point
if level == 0:
topY = y - (size**2 - (size/2)**2)**0.5
canvas.create_polygon(x, y, x+size, y, x+size/2, topY, fill='black')
else:
# Bottom-left triangle
drawSierpinskiTriangle(app, canvas, level-1, x, y, size/2)
# Bottom-right triangle
drawSierpinskiTriangle(app, canvas, level-1, x+size/2, y, size/2)
# Top triangle
midY = y - ((size/2)**2 - (size/4)**2)**0.5
drawSierpinskiTriangle(app, canvas, level-1, x+size/4, midY, size/2)
def keyPressed(app, event):
if event.key in ['Up', 'Right']:
app.level += 1
elif (event.key in ['Down', 'Left']) and (app.level > 0):
app.level -= 1
def redrawAll(app, canvas):
margin = min(app.width, app.height)//10
x, y = margin, app.height-margin
size = min(app.width, app.height) - 2*margin
drawSierpinskiTriangle(app, canvas, app.level, x, y, size)
canvas.create_text(app.width/2, 0,
text = f'Level {app.level} Fractal',
font = 'Arial ' + str(int(margin/3)) + ' bold',
anchor='n')
canvas.create_text(app.width/2, margin,
text = 'Use arrows to change level',
font = 'Arial ' + str(int(margin/4)),
anchor='s')
runApp(width=400, height=400)
Result:

Side-by-Side Levels:
from cmu_112_graphics import *
def appStarted(app):
app.level = 1
def keyPressed(app, event):
if event.key in ['Up', 'Right']:
app.level += 1
elif (event.key in ['Down', 'Left']) and (app.level > 0):
app.level -= 1
def drawSierpinskiTriangle(app, canvas, level, x, y, size):
# (x,y) is the lower-left corner of the triangle
# size is the length of a side
# Need a bit of trig to calculate the top point
if level == 0:
topY = y - (size**2 - (size/2)**2)**0.5
canvas.create_polygon(x, y, x+size, y, x+size/2, topY, fill='black')
else:
# Bottom-left triangle
drawSierpinskiTriangle(app, canvas, level-1, x, y, size/2)
# Bottom-right triangle
drawSierpinskiTriangle(app, canvas, level-1, x+size/2, y, size/2)
# Top triangle
midY = y - ((size/2)**2 - (size/4)**2)**0.5
drawSierpinskiTriangle(app, canvas, level-1, x+size/4, midY, size/2)
# Add circles around app.level (left side) to show how
# level N is made up of 3 level N-1's:
if (level == app.level):
h = size * 3**0.5/2
cx, cy, r = x+size/2, y-h/3, size/3**0.5
canvas.create_oval(cx-r, cy-r, cx+r, cy+r,
fill=None, outline='pink')
def drawLevel(app, canvas, level, cx):
margin = min(app.width, app.height)//10
size = min(app.width, app.height) - 2*margin
x, y = cx-size/2, app.height-margin
drawSierpinskiTriangle(app, canvas, level, x, y, size)
canvas.create_text(cx, 0,
text = f'Level {level} Fractal',
font = 'Arial ' + str(int(margin/3)) + ' bold',
anchor='n')
canvas.create_text(cx, margin,
text = 'Use arrows to change level',
font = 'Arial ' + str(int(margin/4)),
anchor='s')
def redrawAll(app, canvas):
drawLevel(app, canvas, app.level, app.width/4)
drawLevel(app, canvas, app.level+1, app.width*3/4)
# draw the right arrow between the levels
canvas.create_text(app.width/2, app.height/2, text=u'\u2192',
font='Arial 50 bold')
runApp(width=800, height=400)
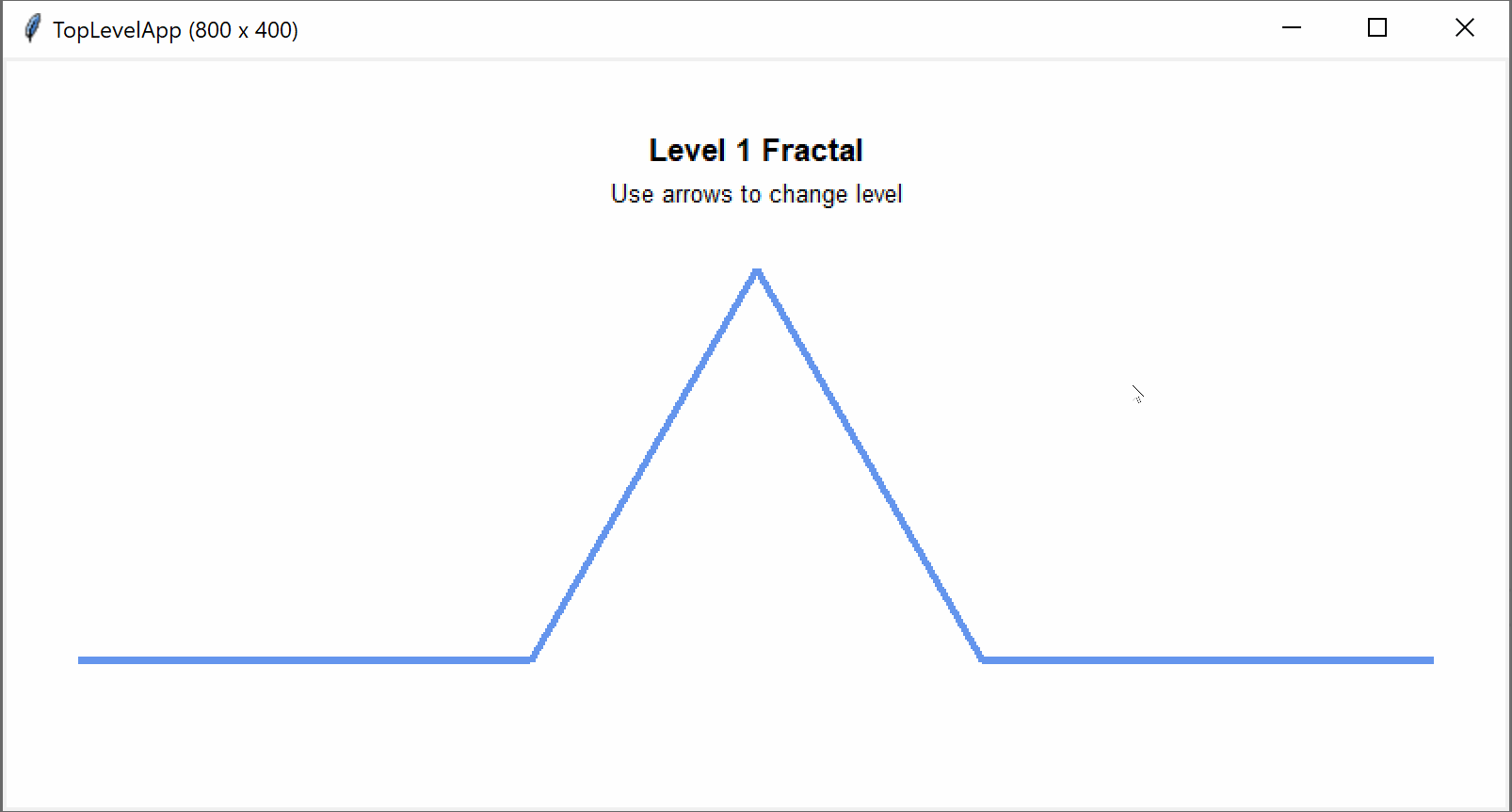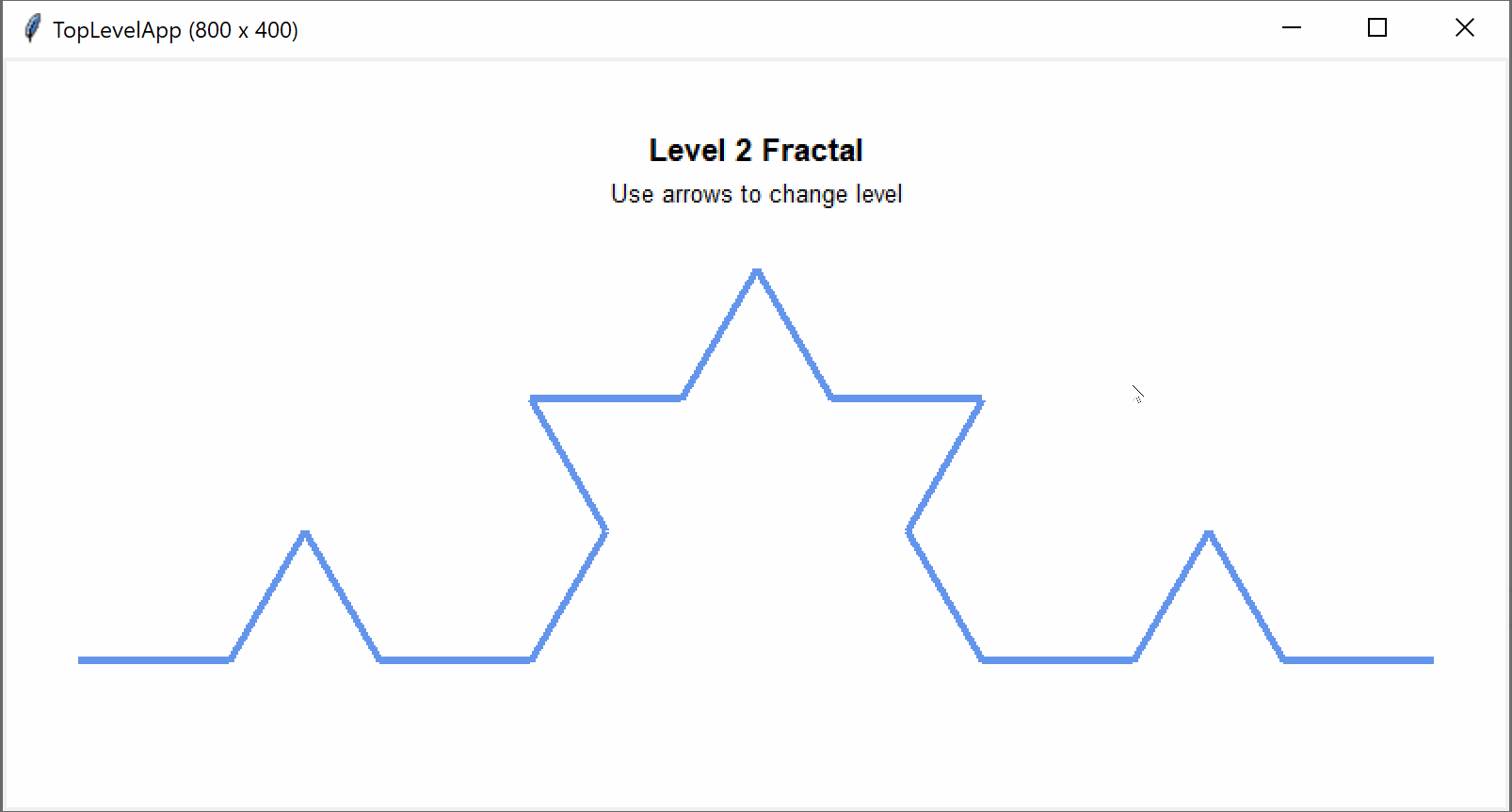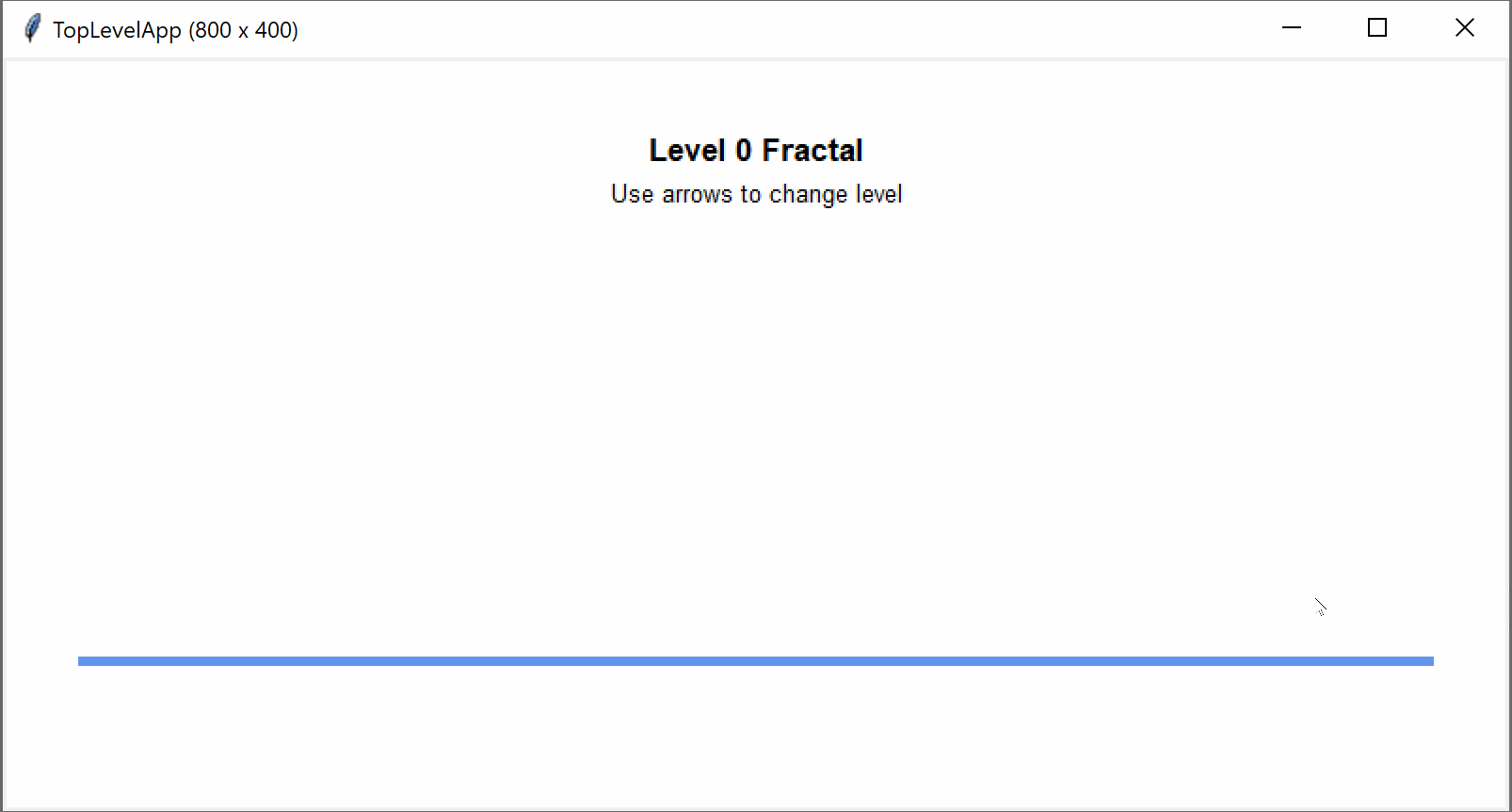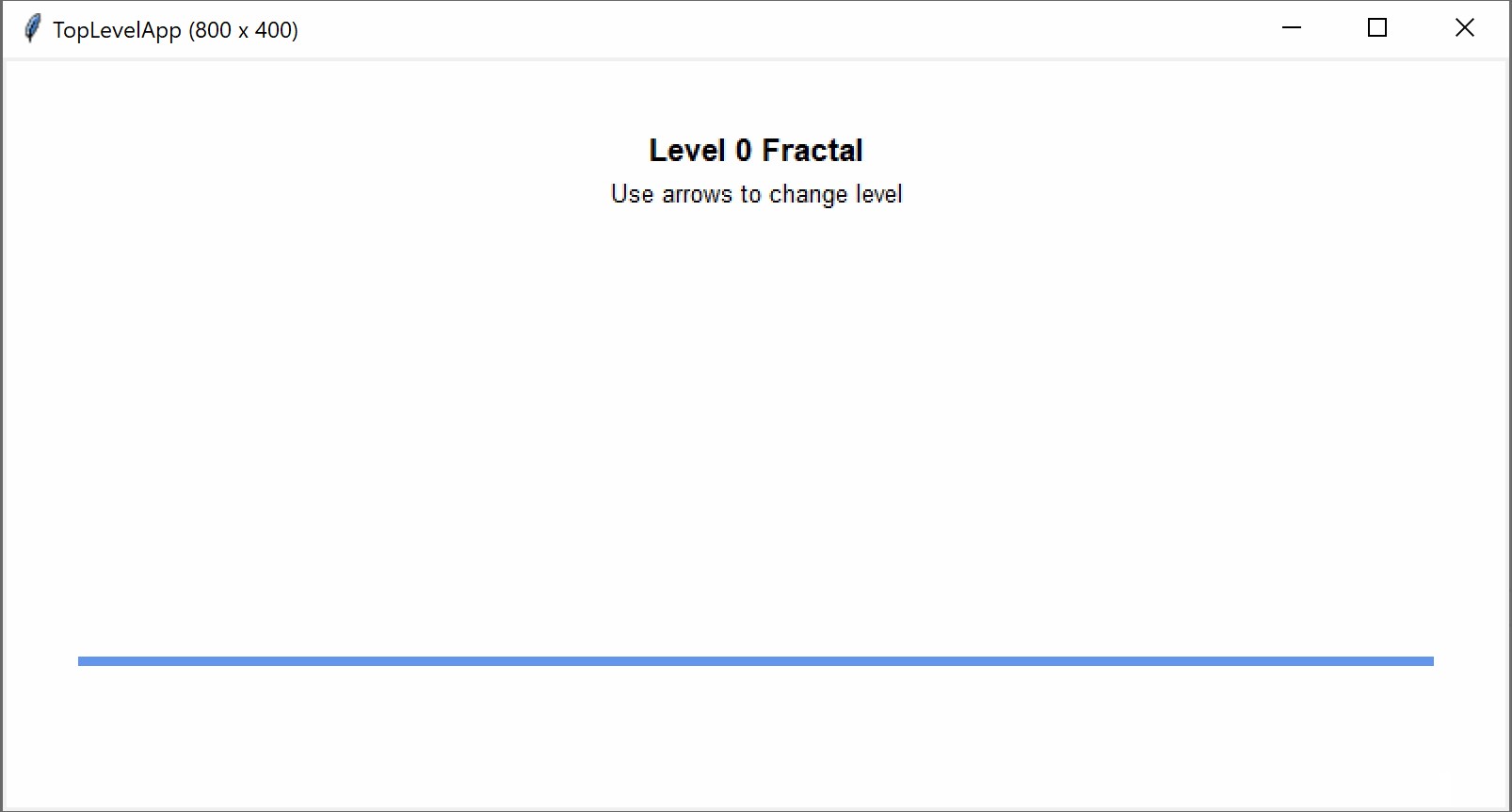
from cmu_112_graphics import *
import math
def newKochCurvePoints(start, end):
# Return three new points that will form the four new lines
# Lines:
# start -> point1 (first third or orginal)
# point1 -> point2
# point2 -> point3
# point3 -> end (last third or orginal)
# Point1
# One third of the way from start to end
point1x = (end[0]-start[0])*1/3 + start[0]
point1y = (end[1]-start[1])*1/3 + start[1]
point1 = (point1x, point1y)
# Point3
# Two thirds of the way from start to end
point3x = (end[0]-start[0])*2/3 + start[0]
point3y = (end[1]-start[1])*2/3 + start[1]
point3 = (point3x, point3y)
# Point2
# Start with halfway between start and end
point2x = (end[0]-start[0])*1/2 + start[0]
point2y = (end[1]-start[1])*1/2 + start[1]
# perpendicular change, scaled appropriately
dy = -(end[0]-start[0])
dx = (end[1]-start[1])
scale = math.sqrt((1/3)**2 - (1/6)**2)/1
point2x += scale*dx
point2y += scale*dy
point2 = (point2x, point2y)
return (point1, point2, point3)
def appStarted(app):
app.level = 0
def drawFractal(app, canvas, level, start, end):
dist = math.sqrt((end[0]-start[0])**2 + (end[1]-start[1])**2)
if level == 0 or dist <= 1:
canvas.create_line(start[0], start[1], end[0], end[1])
else:
point1, point2, point3 = newKochCurvePoints(start, end)
drawFractal(app, canvas, level-1, start, point1)
drawFractal(app, canvas, level-1, point1, point2)
drawFractal(app, canvas, level-1, point2, point3)
drawFractal(app, canvas, level-1, point3, end)
def keyPressed(app, event):
if event.key in ['Up', 'Right']:
app.level += 1
elif (event.key in ['Down', 'Left']) and (app.level > 0):
app.level -= 1
def redrawAll(app, canvas):
margin = min(app.width, app.height)//10
start = (margin, app.height-margin*2)
end = (app.width-margin, app.height-margin*2)
drawFractal(app, canvas, app.level, start, end)
canvas.create_text(app.width/2, 0,
text = f'Level {app.level} Fractal',
font = 'Arial ' + str(int(margin/3)) + ' bold',
anchor='n')
canvas.create_text(app.width/2, margin,
text = 'Use arrows to change level',
font = 'Arial ' + str(int(margin/4)),
anchor='s')
runApp(width=800, height=400)
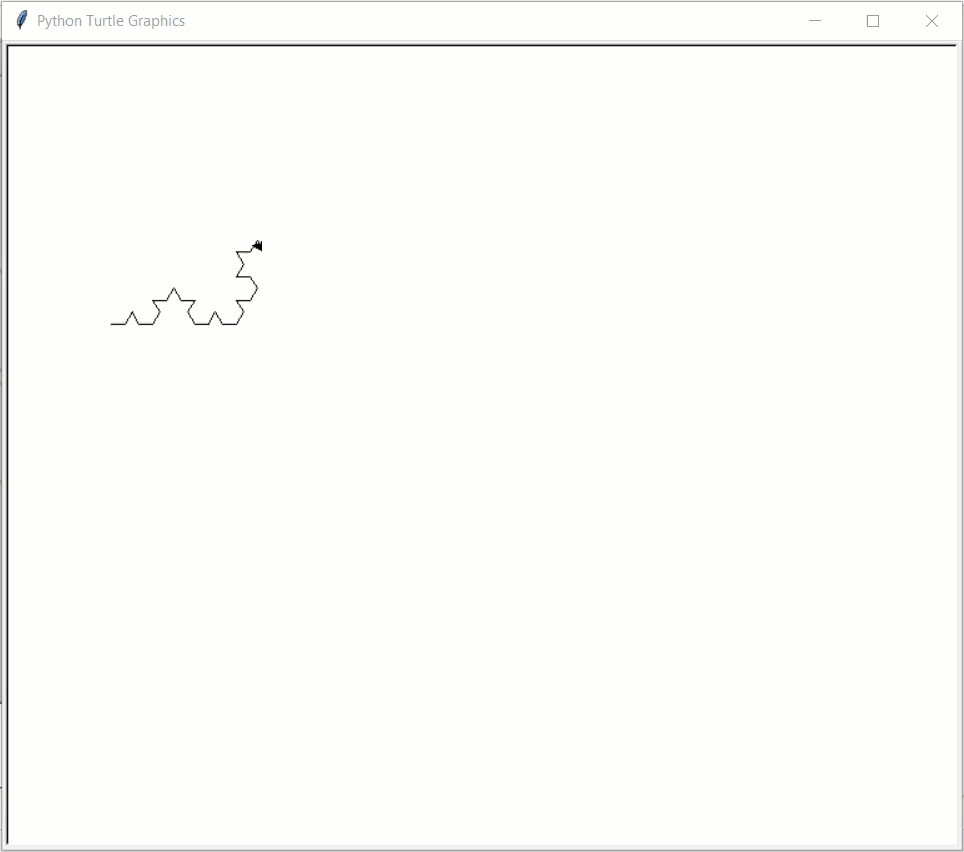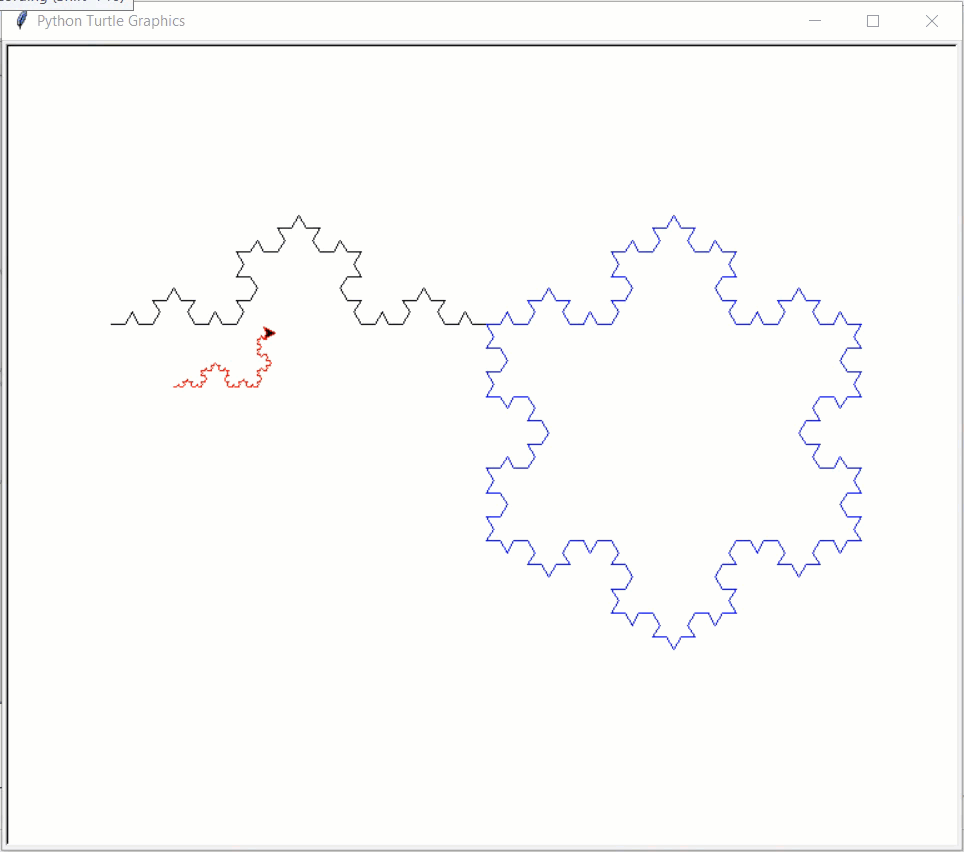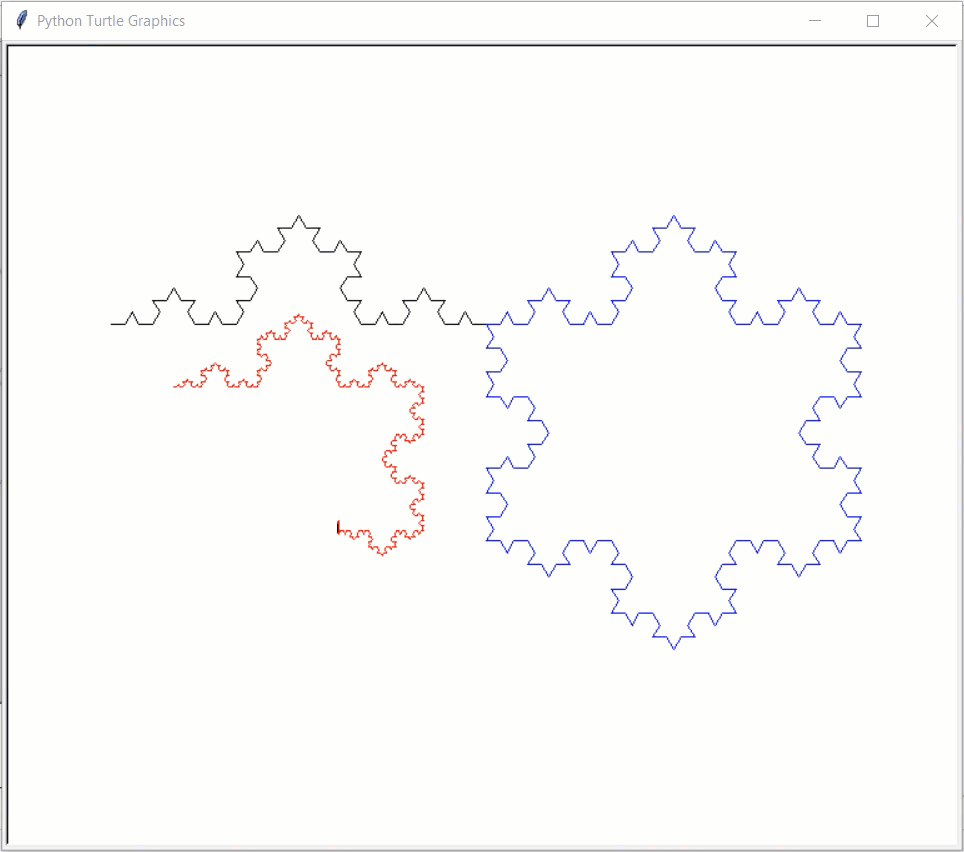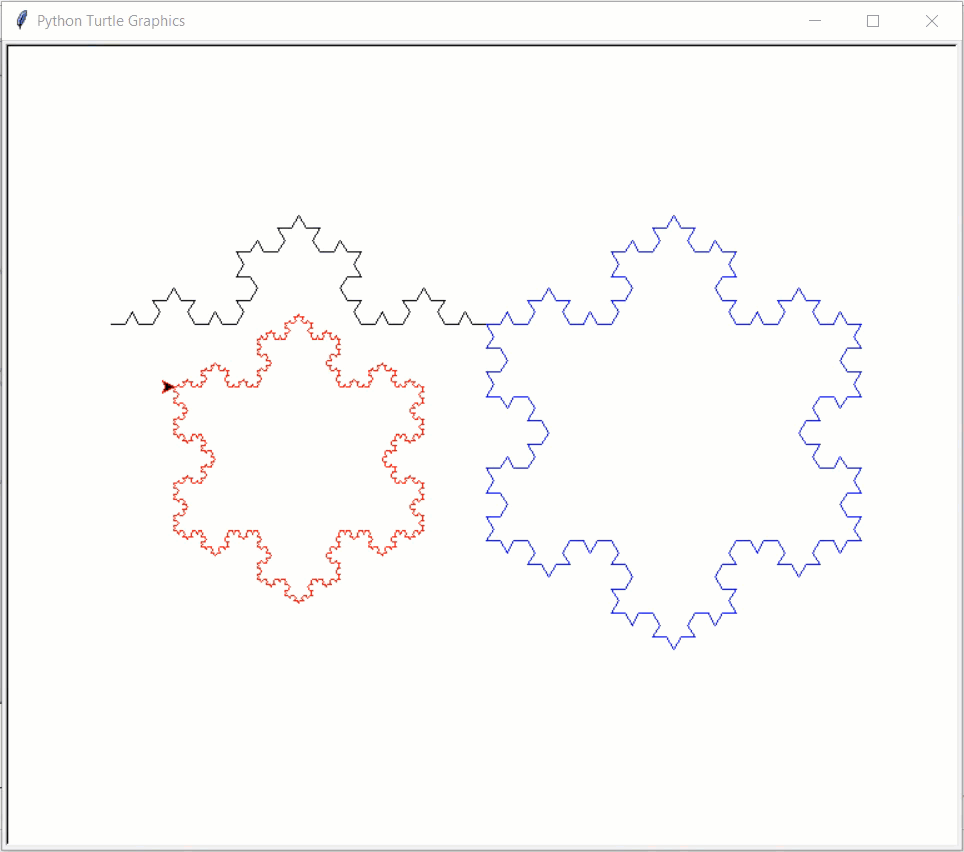
# This example uses turtle graphics, not Tkinter
import turtle
def drawKochSide(length, level):
if (level == 1):
turtle.forward(length)
else:
drawKochSide(length/3, level-1)
turtle.left(60)
drawKochSide(length/3, level-1)
turtle.right(120)
drawKochSide(length/3, level-1)
turtle.left(60)
drawKochSide(length/3, level-1)
def drawKochSnowflake(length, level):
for step in range(3):
drawKochSide(length, level)
turtle.right(120)
def drawKochExamples():
turtle.delay(1)
turtle.speed(0)
turtle.penup()
turtle.goto(-300,100)
turtle.pendown()
turtle.pencolor('black')
drawKochSide(300, 4)
turtle.pencolor('blue')
drawKochSnowflake(300, 4)
turtle.penup()
turtle.goto(-250,50)
turtle.pendown()
turtle.pencolor('red')
drawKochSnowflake(200, 5)
turtle.done()
drawKochExamples()
Result:
Key excerpt:
def solveMaze(app):
visited = set()
path = []
return solve(app, path, visited, 0,0), visited
def solve(app, path, visited, row, col):
maze = app.maze
rows, cols = len(maze), len(maze[0])
targetRow, targetCol = rows-1, cols-1
# Base case: Return None if we've already been here
if (row, col) in visited:
return None
# Add the new location
visited.add((row, col))
path.append((row, col))
# Base case: Return visited if we found the solution
if (row, col)==(targetRow, targetCol):
return path
# Recursive case: Search through next valid directions
else:
for drow, dcol in [app.north, app.south, app.east, app.west]:
if isValid(app, row, col, (drow, dcol)):
result = solve(app, path, visited, row+drow, col+dcol)
if result != None:
return result
# Backtrack if no solution found
#visited.remove((row, col))
path.pop()
return None
Key excerpt:
def nQueens(n):
# Set up an empty board and call our recursive solver
board = [['_']*n for row in range(n)]
return nQueensSolver(board, 0)
def nQueensSolver(board, newQueenRow):
rows, cols = len(board), len(board[0])
if newQueenRow >= rows: # If we are trying to place beyond the board...
return board # ...we're all done! Return the solution.
else:
# For each column in newQueenRow...
for newQueenCol in range(cols):
if isLegalMove(board, newQueenRow, newQueenCol):
# Make the move if it is legal.
board[newQueenRow][newQueenCol] = 'Q'
# Recursively try to solve from this point
result = nQueensSolver(board, newQueenRow + 1)
if result != None: # Return the solution if we found one
return result
# Undo the move if we did not find a solution
board[newQueenRow][newQueenCol] = '_'
return None # Return None if no moves lead to a solution
Memoization is a general technique to make certain recursive applications more efficient. The Big idea: when a program does a lot of repetitive computation, store results as they are computed, then look up and reuse results when available.