Inverting the Eikonal Equation
Using PDE-Constrained Optimization
Arjun Teh
Outline
- The eikonal equation and its inverse
- Solving the inverse problem
- The discrete version
The Eikonal Equation
Scenarios with eikonal
- Gas Flow Reconstruction
- GRIN Lens
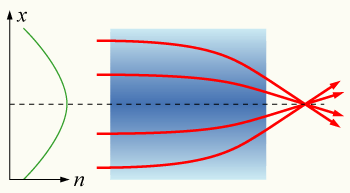
Describes the geometric properties of a wave with small wavelength moving through a medium
The Forward Problem
The eikonal equation is a PDE
∥∇Φ∥2=η2
\lVert \nabla \Phi \rVert^2 = \eta^2
Given a refractive index field, η, what is a configuration, Φ, that satisfies the above equation?
Φ is the phase of the wavefront, and ∇Φ describes how rays will propagate through the volume
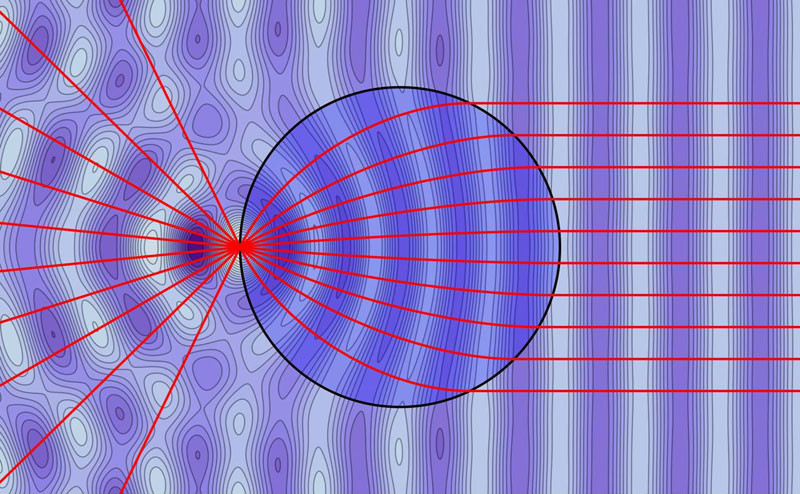
The Forward Problem
The eikonal equation can be solved in different ways
- Fast Marching (wave propagation)
- Raytracing (ray marching)
All of them solve for the phase (Φ) given the underlying refractive field (η)
The Inverse Problem
"I want to find the refractive field, η, that will admit the configuration, Φ, that I observed/desire"
ηmin​∫dΩ​(Φ−Φobserved​)2
\underset{\eta}{\text{min}} {\displaystyle \int_{d\Omega}} \left(\Phi - \Phi_{observed} \right)^2
s.t. ∥∇Φ∥2−η2=0
s.t. ~~\lVert \nabla \Phi \rVert^2 - \eta^2 = 0
Reframe the optimization
ηmin​∫dΩ​(Φ−Φobserved​)2
\underset{\eta}{\text{min}} {\displaystyle \int_{d\Omega}} \left(\Phi - \Phi_{observed} \right)^2
s.t. ∥∇Φ∥2−η2=0
s.t. ~~\lVert \nabla \Phi \rVert^2 - \eta^2 = 0
η,λ,Φmin​ C(η)
\underset{\eta, \lambda, \Phi}{\text{min}} ~~\mathcal{C}(\eta)
−∫Ω​λ(∥∇Φ∥2−η2)
- {\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right)
C(Φ(η))
\mathcal{C}(\Phi(\eta))
Reframe the optimization
η,λ,Φmin​ C(Φ(η))
\underset{\eta, \lambda, \Phi}{\text{min}} ~~\mathcal{C}(\Phi(\eta))
−∫Ω​λ(∥∇Φ∥2−η2)
- {\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right)
L(η,λ,Φ)
\mathcal{L}(\eta, \lambda, \Phi)
With this formulation, we can conceptually treat η,λ, and Φ as independent variables.
If we want to do gradient descent, our new optimization problem will be equivalent to our original problem if we insist that λ and Φ are critical points of L.
Reframe the optimization
dηd​C(Φ(η))=dηd​L(η,λ∗,Φ∗)
\frac{d}{d\eta}\mathcal{C}(\Phi(\eta)) = \frac{d}{d\eta}\mathcal{L}(\eta, \lambda^*, \Phi^*)
dλdL(η,λ∗,Φ∗)​=dΦdL(η,λ∗,Φ∗)​=0
\frac{d\mathcal{L}(\eta, \lambda^*, \Phi^*)}{d\lambda} = \frac{d\mathcal{L}(\eta, \lambda^*, \Phi^*)}{d\Phi} = 0
where,
Finding Φ∗
L=C(Φ)−∫Ω​λ(∥∇Φ∥2−η2)
\mathcal{L} = \mathcal{C}(\Phi) - {\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right)
dλdL​=−∫Ω​(∥∇Φ∥2−η2)=0
\frac{d\mathcal{L}}{d\lambda} = - {\displaystyle \int_{\Omega}} \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right) = 0
Solving the original forward problem yields a critical point with respect to λ.
Finding λ∗
L=C(Φ)−∫Ω​λ(∥∇Φ∥2−η2)
\mathcal{L} = \mathcal{C}(\Phi) - {\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right)
dΦdC​−dΦd​∫Ω​λ(∥∇Φ∥2−η2)=0
\frac{d\mathcal{C}}{d\Phi} - \frac{d}{d\Phi}{\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right) = 0
Assuming we have Φ, we can solve for λ
dΦdL​=
\frac{d\mathcal{L}}{d\Phi} =
Finding λ∗
dΦdC​−dΦd​∫Ω​λ(∥∇Φ∥2−η2)=0
\frac{d\mathcal{C}}{d\Phi} - \frac{d}{d\Phi}{\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right) = 0
dΦdC​−∫Ω​λdΦd​(∥∇Φ∥2−η2)=0
\frac{d\mathcal{C}}{d\Phi} - {\displaystyle \int_{\Omega}} \lambda \frac{d}{d\Phi} \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right) = 0
dΦdC​−∫Ω​λdΦd​∥∇Φ∥2=0
\frac{d\mathcal{C}}{d\Phi} - {\displaystyle \int_{\Omega}} \lambda \frac{d}{d\Phi} \lVert \nabla \Phi \rVert^2 = 0
Finding λ∗
dΦdC​−∫Ω​λdΦd​∥∇Φ∥2=0
\frac{d\mathcal{C}}{d\Phi} - {\displaystyle \int_{\Omega}} \lambda \frac{d}{d\Phi} \lVert \nabla \Phi \rVert^2 = 0
dΦdC​−∫Ω​λ2(∇Φ)T(d∇Φ)=0
\frac{d\mathcal{C}}{d\Phi} - {\displaystyle \int_{\Omega}} \lambda 2\left( \nabla \Phi \right)^T \left(d\nabla \Phi\right) = 0
dxd∥x∥2​=2xT
\frac{d\lVert x \rVert^2}{dx} = 2x^T
dΦdC​−∫Ω​λ2(∇Φ)T(∇dΦ)=0
\frac{d\mathcal{C}}{d\Phi} - {\displaystyle \int_{\Omega}} \lambda 2\left( \nabla \Phi \right)^T \left(\nabla d\Phi\right) = 0
Finding λ∗
dΦd​∫∂Ω​(Φ−Φ^)2−2∫Ω​λ(∇Φ)T(∇dΦ)=0
\frac{d}{d\Phi} {\displaystyle \int_{\partial\Omega}} \left(\Phi - \hat{\Phi}\right)^2 - 2{\displaystyle \int_{\Omega}} \lambda \left( \nabla \Phi \right)^T \left(\nabla d\Phi\right) = 0
∫∂Ω​2(Φ−Φ^)dΦ−2∫Ω​λ(∇Φ)T(∇dΦ)=0
{\displaystyle \int_{\partial\Omega}} 2\left(\Phi - \hat{\Phi}\right)d\Phi - 2{\displaystyle \int_{\Omega}} \lambda \left( \nabla \Phi \right)^T \left(\nabla d\Phi\right) = 0
dΦdC​−∫Ω​λ2(∇Φ)T(∇dΦ)=0
\frac{d\mathcal{C}}{d\Phi} - {\displaystyle \int_{\Omega}} \lambda 2\left( \nabla \Phi \right)^T \left(\nabla d\Phi\right) = 0
Finding λ∗
∫∂Ω​2(Φ−Φ^)dΦ−2∫Ω​λ(∇Φ)T(∇dΦ)=0
{\displaystyle \int_{\partial\Omega}} 2\left(\Phi - \hat{\Phi}\right)d\Phi - 2{\displaystyle \int_{\Omega}} \lambda \left( \nabla \Phi \right)^T \left(\nabla d\Phi\right) = 0
∫Ω​∇uTF=∫∂Ω​u(FTn^)−∫Ω​u(∇⋅F)
{\displaystyle \int_{\Omega}} \nabla u^T \mathbf{F}
= {\displaystyle \int_{\partial\Omega}} u\left( \mathbf{F}^T \mathbf{\hat{n}}\right)
- {\displaystyle \int_{\Omega}} u(\nabla \cdot \mathbf{F})
F=λ∇Φ
\mathbf{F} = \lambda \nabla \Phi
u=dΦ
u = d\Phi
Using Divergence Theorem:
∫∂Ω​(λ∇Φ)Tn^dΦ−∫Ω​∇⋅λ(∇Φ)dΦ
{\displaystyle \int_{\partial\Omega}} \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}} d\Phi - {\displaystyle \int_{\Omega}} \nabla \cdot \lambda \left( \nabla \Phi \right) d\Phi
Finding λ∗
∫∂Ω​2(Φ−Φ^)dΦ−2∫Ω​λ(∇Φ)T(∇dΦ)=0
{\displaystyle \int_{\partial\Omega}} 2\left(\Phi - \hat{\Phi}\right)d\Phi - 2{\displaystyle \int_{\Omega}} \lambda \left( \nabla \Phi \right)^T \left(\nabla d\Phi\right) = 0
0=∫∂Ω​(Φ−Φ^)dΦ−(∫∂Ω​(λ∇Φ)Tn^dΦ−∫Ω​∇⋅λ(∇Φ)dΦ)
0 = {\displaystyle \int_{\partial\Omega}} \left(\Phi - \hat{\Phi}\right)d\Phi \\
- \left({\displaystyle \int_{\partial\Omega}} \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}} d\Phi - {\displaystyle \int_{\Omega}} \nabla \cdot \lambda \left( \nabla \Phi \right) d\Phi \right)
Finding λ∗
0=∫∂Ω​(Φ−Φ^)dΦ−(∫∂Ω​(λ∇Φ)Tn^dΦ−∫Ω​∇⋅λ(∇Φ)dΦ)
0 = {\displaystyle \int_{\partial\Omega}} \left(\Phi - \hat{\Phi}\right) d\Phi\\
- \left({\displaystyle \int_{\partial\Omega}} \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}} d\Phi - {\displaystyle \int_{\Omega}} \nabla \cdot \lambda \left( \nabla \Phi \right) d\Phi \right)
∫∂Ω​(Φ−Φ^)dΦ−∫∂Ω​(λ∇Φ)Tn^dΦ=0
{\displaystyle \int_{\partial\Omega}} \left(\Phi - \hat{\Phi}\right) d\Phi
- {\displaystyle \int_{\partial\Omega}} \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}} d\Phi = 0
∫Ω​∇⋅λ(∇Φ)dΦ=0
{\displaystyle \int_{\Omega}} \nabla \cdot \lambda \left( \nabla \Phi \right) d\Phi = 0
Finding λ∗
∫∂Ω​(Φ−Φ^)dΦ−∫∂Ω​(λ∇Φ)Tn^dΦ=0
{\displaystyle \int_{\partial\Omega}} \left(\Phi - \hat{\Phi}\right)d\Phi
- {\displaystyle \int_{\partial\Omega}} \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}} d\Phi = 0
∫Ω​∇⋅λ(∇Φ)dΦ=0
{\displaystyle \int_{\Omega}} \nabla \cdot \lambda \left( \nabla \Phi \right) d\Phi = 0
In order for both of these equations to be true, they need to be true for the whole domain of the integral
Finding λ∗
(Φ−Φ^)=(λ∇Φ)Tn^; on ∂Ω
\left(\Phi - \hat{\Phi}\right)
= \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}}; ~\text{on}~ \partial \Omega
∇⋅λ(∇Φ)=0; on Ω
\nabla \cdot \lambda \left( \nabla \Phi \right)= 0; ~\text{on}~ \Omega
This is known as the adjoint equation, and λ is referred to as the adjoint state.
Recap so far
dλdL​=0
\frac{d\mathcal{L}}{d\lambda} = 0
∫Ω​(∥∇Φ∥2−η2)=0
{\displaystyle \int_{\Omega}} \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right) = 0
dΦdL​=0
\frac{d\mathcal{L}}{d\Phi} = 0
(Φ−Φ^)=(λ∇Φ)Tn^; on ∂Ω
\left(\Phi - \hat{\Phi}\right)
= \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}}; ~\text{on}~ \partial \Omega
∇⋅λ(∇Φ)=0; on Ω
\nabla \cdot \lambda \left( \nabla \Phi \right)= 0; ~\text{on}~ \Omega
Forward System
Adjoint System
The Adjoint State
We now know Φ∗ and λ∗ by solving for the stationary points.
L=∫∂Ω​(Φ−Φ^)2−∫Ω​λ(∥∇Φ∥2−η2)
\mathcal{L} = {\displaystyle \int_{\partial\Omega}} (\Phi - \hat{\Phi})^2 - {\displaystyle \int_{\Omega}} \lambda \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right)
dηd​L=∫Ω​λ(−dηd​η2)
\frac{d}{d\eta}\mathcal{L} = {\displaystyle \int_{\Omega}} \lambda \left( - \frac{d}{d\eta}\eta^2 \right)
The Adjoint State
We now know Φ∗ and λ∗ by solving for the stationary points.
dηd​L=∫Ω​λ(−dηd​η2)
\frac{d}{d\eta}\mathcal{L} = {\displaystyle \int_{\Omega}} \lambda \left( - \frac{d}{d\eta}\eta^2 \right)
dηd​L=−∫Ω​2λη
\frac{d}{d\eta}\mathcal{L} = -{\displaystyle \int_{\Omega}} 2\lambda \eta
The Adjoint State
To solve the problem:
dηd​L=−∫Ω​2λη
\frac{d}{d\eta}\mathcal{L} = -{\displaystyle \int_{\Omega}} 2\lambda \eta
ηmin​ L(η,λ∗,Φ∗)
\underset{\eta}{\text{min}} ~~\mathcal{L}\left(\eta, \lambda^*, \Phi^* \right)
We can use these equations:
∫Ω​(∥∇Φ∥2−η2)=0
{\displaystyle \int_{\Omega}} \left( \lVert \nabla \Phi \rVert^2 - \eta^2 \right) = 0
(Φ−Φ^)=(λ∇Φ)Tn^; on ∂Ω
\left(\Phi - \hat{\Phi}\right)
= \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}}; ~\text{on}~ \partial \Omega
∇⋅λ(∇Φ)=0; on Ω
\nabla \cdot \lambda \left( \nabla \Phi \right)= 0; ~\text{on}~ \Omega
Using the adjoint
Using a known light source, or initial conditions, we can use the adjoint system to guess what the refractive index is and then refine the guess using gradient descent.
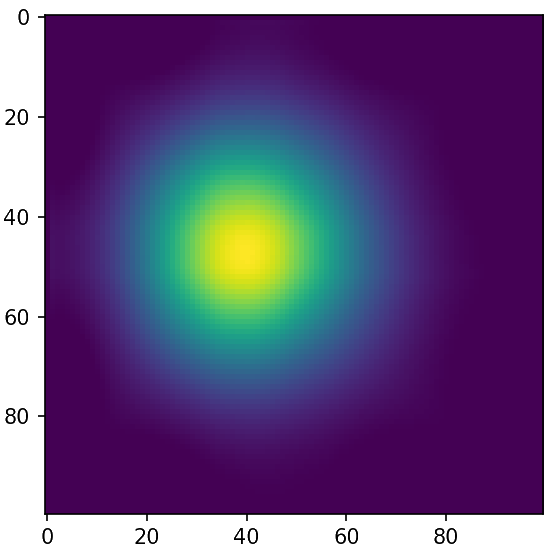
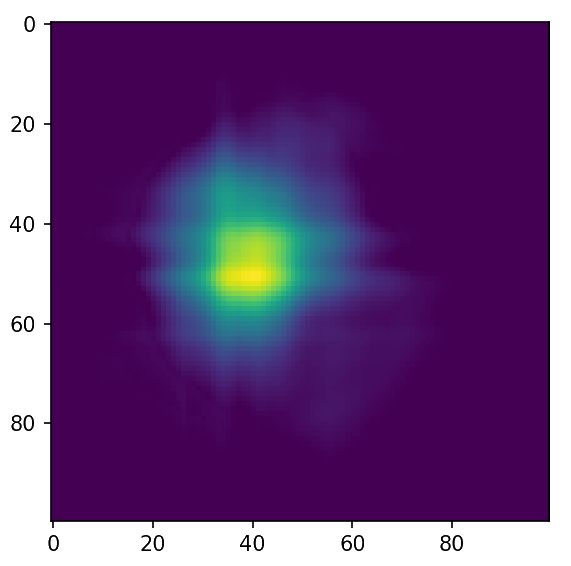
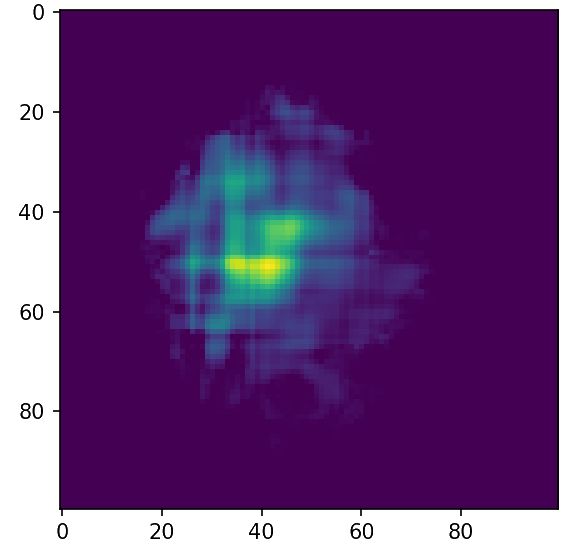
Back to the adjoint equation
λ is effectively the derivative we are looking for.
What does it represent conceptually?
(Φ−Φ^)=(λ∇Φ)Tn^; on ∂Ω
\left(\Phi - \hat{\Phi}\right)
= \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}}; ~\text{on}~ \partial \Omega
∇⋅λ(∇Φ)=0; on Ω
\nabla \cdot \lambda \left( \nabla \Phi \right)= 0; ~\text{on}~ \Omega
Back to the adjoint equation
The observed residual only contributes to λ along the normal of our volume
In other words, measurements that are parallel to the direction of rays will give us the most contribution to the derivative.
(Φ−Φ^)=(λ∇Φ)Tn^; on ∂Ω
\left(\Phi - \hat{\Phi}\right)
= \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}}; ~\text{on}~ \partial \Omega
∇⋅λ(∇Φ)=0; on Ω
\nabla \cdot \lambda \left( \nabla \Phi \right)= 0; ~\text{on}~ \Omega
Back to the adjoint equation
Expanding the above equation with product rule, yields:
∇λT∇Φ+λΔΦ=0
\nabla \lambda^T \nabla \Phi + \lambda \Delta \Phi = 0
One way to interpret this is that the adjoint state propagates parallel to the rays traveling through the medium
(Φ−Φ^)=(λ∇Φ)Tn^; on ∂Ω
\left(\Phi - \hat{\Phi}\right)
= \left(\lambda \nabla \Phi\right)^T \mathbf{\hat{n}}; ~\text{on}~ \partial \Omega
∇⋅λ(∇Φ)=0; on Ω
\nabla \cdot \lambda \left( \nabla \Phi \right)= 0; ~\text{on}~ \Omega
Back to the adjoint equation
∇λT∇Φ+λΔΦ=0
\nabla \lambda^T \nabla \Phi + \lambda \Delta \Phi = 0
Solving the adjoint can then be described as propagating rays through the medium and then backtracing the residual value back through the volume.
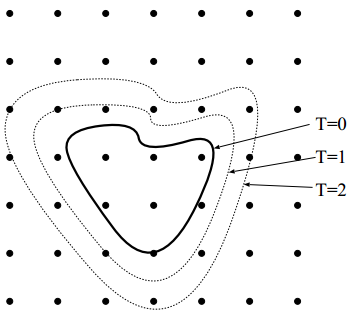
The discrete adjoint
If we instead use a discretized version of the eikonal equation, our Lagrangian becomes
L=i∈meas∑​(Φi​−Φ^i​)2−i∈Ω∑​λi​((Dx​Φi​)2+(Dy​Φi​)2−ηi2​)
\mathcal{L} = \underset{i \in \text{meas}}{\sum} \left(\Phi_i - \hat{\Phi}_i \right)^2 \\
- \underset{i \in \Omega}{\sum} \lambda_i \left((\mathbf{D}_x\Phi_i)^2 + (\mathbf{D}_y \Phi_i)^2 - \eta^2_i \right)
We differentiate with respect to each Φi​ and λi​ to get a linear system
The discrete adjoint
L=i∈meas∑​(Φi​−Φ^i​)2−i∈Ω∑​λi​((Dx​Φi​)2+(Dy​Φi​)2−ηi2​)
\mathcal{L} = \underset{i \in \text{meas}}{\sum} \left(\Phi_i - \hat{\Phi}_i \right)^2 \\
- \underset{i \in \Omega}{\sum} \lambda_i \left((\mathbf{D}_x\Phi_i)^2 + (\mathbf{D}_y \Phi_i)^2 - \eta^2_i \right)
[0Φ−Φ^​]−⎣⎢⎢⎢⎡​dΦ0T​dΦ1T​⋯dΦiT​​⎦⎥⎥⎥⎤​λ=0
\begin{bmatrix}
0 \\
\Phi - \hat{\Phi}
\end{bmatrix} -
\begin{bmatrix}
d\Phi_0^T \\ d\Phi_1^T \\ \cdots \\ d\Phi_i^T
\end{bmatrix} \lambda = 0
λ here acts exactly in the same way as the continuous version
Concluding Thoughts
- Adjoint State Method is Lagrange Multipliers in disguise
- The broad theory for the adjoint state method can be used to tackle inverse problems
- The adjoint state in the eikonal case amounts to backtracing rays back through the volume to deposit the gradient value
References and Links
- Nice explanation of the adjoint state:
- Presentation on Cea's Method for shape optimization:
- Adjoint State Method used in tomography
Inverting the Eikonal Equation Using PDE-Constrained Optimization Arjun Teh