In many problems we are required to test a hypothesis about a population mean. Typical examples:
In each case there is a null hypothesis that the population mean of a random variable $X$ is $\mu_0$. Our alternate hypothesis contradicts this null hypothesis. We may make a one-sided counter claim, e.g. that the actual population mean is greater than $\mu_0$, or it may be two-sided, where our counter claim is merely that the real population mean $\mu$ is not equal to $\mu_0$, but may be greater or lesser.
The testing procedure samples $N$ instances of data (e.g. $N$ bulbs, or $N$ movies) and obtains $N$ readings $X_1, X_2, \cdots, X_N$. For the bulbs example, $X$ is the life expectancy of a bulb, and $X_1, \cdots, X_N$ are the be the observed life of the $N$ bulbs. For the movies, $X_1, \cdots, X_N$ may be the actual error between the predicted and true ratings of the $N$ movies.
From these $N$ samples, we compute a sample mean $Y = \frac{1}{N}\sum_{i=1}^N X_i$. We will now conduct the test as follows.
Large sample tests
We first deal with the case where the number of samples $N$ is large (at least 100). We will address the issue of smaller sample sizes below.
We note that $Y$ is a point estimate of the mean of the probability distribution of $X$. As we saw in the discussion of point estimators, the expected value of $Y$ is the true mean of the distribution: $E[Y] = \mu$ and the variance of $Y$ is $var(Y) = \frac{1}{N}\sigma^2$, where $\sigma^2$ is the true variance of $X$.
Under the null hypothesis, $\mu = \mu_0$. In some cases, the null hypothesis may also propose a value $\sigma_0^2$ for the true variance of $X$ (e.g. the manufacturer may claim that the mean life of bulbs is 1000 hours with a standard deviation of 100 hours). Thus, under the null hypothesis, $E[Y] = \mu_0$ and $var(Y) = \frac{\sigma_0^2}{N}$, and $stdev(Y) = \frac{\sigma_0}{\sqrt{N}}$.
We can now define the following normalized statistic, which can be computed from $Y$ and the parameters proposed by the null hypothesis: \[ Z = \frac{Y - E[Y]}{stdev(Y)} \\ = \frac{Y - \mu_0}{\frac{\sigma_0}{\sqrt{N}}} \]
More commonly, however, the variance $\sigma_0^2$ of the variable being tested will not be specified under the null hypothesis. For large enough $N$ ($N > 100$), we can use the point estimate $\hat{\sigma}^2_N = \frac{1}{N-1}(X_i - Y)^2$, instead. In this case, we must define \[ Z = \frac{Y - \mu_0}{\frac{\hat{\sigma}_N}{\sqrt{N}}} \]
From the central limit theorem, we know that the PDF of $Z$ is a standard normal. So, we can now operate directly on $Z$ to conduct our tests.
Left-sided test: In the left-sided test, our alternate hypothesis is that the true $\mu$ is less than the one proposed by the null hypothesis, $\mu_0$. This claim can be validated if the sample average $Y$ is sufficiently smaller than the proposed mean, $\mu_0$. Alternately, the claim can be validated if $Z$ is sufficiently negative (to the left of 0). We must now find a threshold value $z_\alpha$ such that if $Z \leq z_\alpha$ we can confidently reject the null hypothesis.
We set a desired confidence value, or, alternately, a required upper bound on the probability of type-1 error, $\alpha_z$. Subsequently, we use the standard normal tables to find a threshold $z_\alpha$, such that $\Phi(z_\alpha) = \alpha_z$.
As noted in the discussion on testing Bernoulli variables, the standard normal table only specifies $\Phi(z)$ values for $z \geq 0$. We can nevertheless find the desired $z_\alpha$ value since the standard normal is symmetric. We must find the smallest $C$ such that $\Phi(C) > 1 - \alpha_z$, and set $z_\alpha = -C$.
For example, if we specify that the desired confidence in our test is 95%, i.e. $\alpha_z = 0.05$, we must look up the smallest $C$ value for which $\Phi(C) \geq 0.95$. We find this to be 1.65. Hence $z_\alpha = -1.65$.
We compare the computed $Z$ to this $z_\alpha$. If $Z \leq z_\alpha$, we can conclude that $\mu < \mu_0$ and the null hypothesis can be rejectedisewrong..
Right-sided test: In the right-sided test, our alternate hypothesis is that the true $\mu$ is greater than $\mu_0$. This claim can be validated if the sample average $Y$ is sufficiently greater than $\mu_0$. Alternately, the claim can be validated if $Z$ is sufficiently greater than 0. Hence, we must now find a threshold value $z_\alpha$ such that if $Z \geq z_\alpha$ we can confidently reject the null hypothesis.
Given the specified confidence level, or, alternately, the required upper bound on the probability of type-1 error $\alpha_z$. We use the standard normal tables, which specifies $\Phi(Z)$ values for $Z \geq 0$, to find a threshold $z_\alpha$, such that $1- \Phi(z_\alpha) = \alpha_z$. To do so, we find the smallest $C$ such that $\Phi(C) \geq 1-\alpha_z$ and set $z_\alpha = C$.
If the $Z$ value computed from the samples exceeds $z_\alpha$, i.e. if $Z \geq z_\alpha$, we can reject the null hypothesis with the desired confidence.
For example, if we specify that the desired confidence in our test is 95%, i.e. $\alpha_z = 0.05$, we must look up the smallest $C$ value for which $\Phi(C) \geq 0.95$. We find this to be 1.65. Hence $z_\alpha = 1.65$. If the computed $Z \geq 1.65$, we can conclude that $\mu > \mu_0$ and the null hypothesis can be rejected.
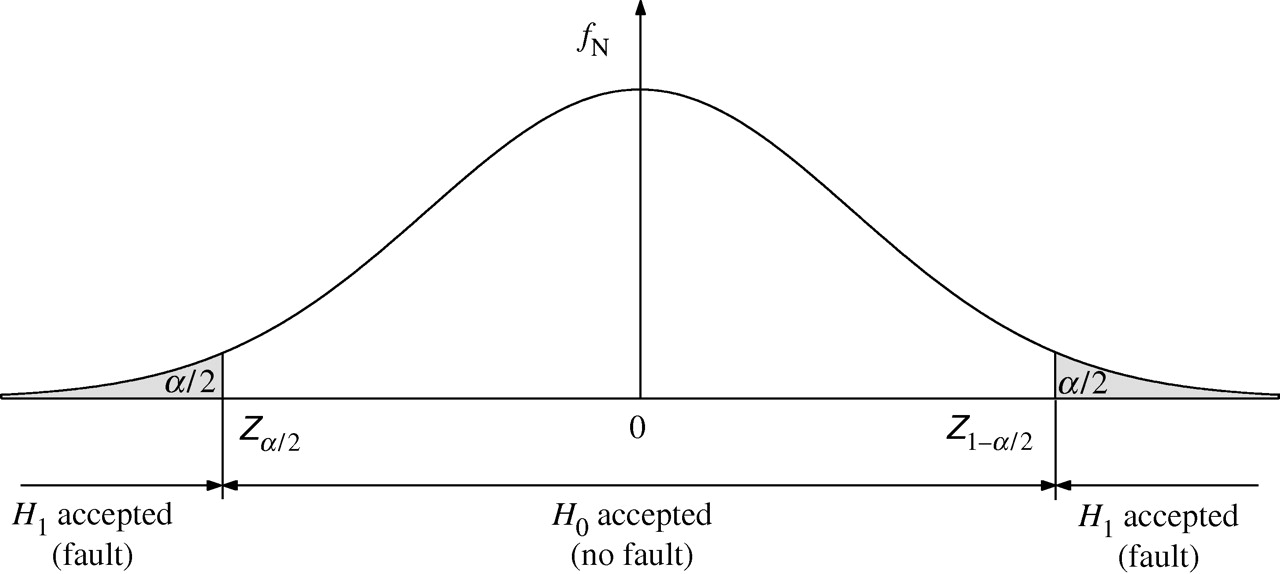
Two-sided test: In the two-sided test our alternate hypothesis is that $\mu \neq \mu_0$, without specifying a direction.
The test for our alternate hypothesis is that if $\mu \neq \mu_0$, $Y$ will not be close to $\mu_0$, and hence $Z$ will not be close to 0. Thus, we must verify that $|Z|$ is greater than a threshold, where the threshold is chosen such that the probability if type-1 error is no larger than a specified $\alpha_z$.
Since the standrd normal is symmetric, $P(|Z| \geq C) = 2 \Phi(C)$ for any $C$ as shown in the figure below.
Caption: $|Y| \geq z_{\frac{\alpha}{2}})$ represents the regions of the axes under the shaded area. The two shaded regions are symmetric, and equal in area. The area of the left shaded region is $\Phi(z_{\frac{\alpha}{2}})$. Thus, $P( |Y| \geq z_{\frac{\alpha}{2}}) = 2\Phi(z_{\frac{\alpha}{2}})$.
Therefore, to find the threshold we must find the smallest $z_{\frac{\alpha}{2}}$ from the normal table (which only shows $\Phi(z)$ values for $z \geq 0$) such that $\Phi(z_{\frac{\alpha}{2}}) \geq 1 - \frac{\alpha_z}{2}$.
We can reject the null hypothesis if $|Z| \geq z_{\frac{\alpha}{2}}$.
For our bulb example, if we desire a confidence of 95%, i.e. $\alpha_z = 0.05$, then $\frac{\alpha}{2} = 0.025$. We must look for the $z_{\frac{\alpha}{2}}$ as the smallest value $C$ where $\Phi(C) \geq 0.975$. Scanning the table, we find that $z_{\frac{\alpha}{2}} = 1.96$. If the magnitude of the $Z$ value computed from the samples exceeds 1.96, we can reject the null hypothesis.
Small sample tests: Using the Student-t
In the discussion on large-sample tests, when the variance of $X$ was not specified by the null hypothesis, we assumed we could estimate it directly from the samples. When $N$ is small, however, the sample variance $\hat{\sigma}_N^2$ is not a good approximation to the true variance of $X$ well. As a result, the PDF of $Z = \frac{Y - \mu}{\frac{\hat{\sigma}_N}{\sqrt{N}}}$ is no longer Gaussian.
In this case, we cannot use the standard normal approximation for the tests. In this case, we must use the student-t. In order to do so, however, we must be reasonably able to assume that the actual distribution of $X$ is Gaussian. Under that assumption the PDF of $Z$ is a student-t with $N-1$ degrees of freedom..
To restate everything explicitly, if we have $N$ samples $X_1, \cdots, X_N$ drawn from a Gaussian with mean $\mu_0$ (as specified by the null hypothesis), then, if we define the statistic \[ Y = \frac{1}{N}\sum_{i=1}^N X_i \] and the estimated variance \[ \hat{\sigma}_N^2 = \frac{1}{N-1}\sum_{i=1}^N(X_i - Y)^2 \] then the variable $Z$ defined as \[ Z = \frac{Y - \mu_0}{\frac{\hat{\sigma}_N}{\sqrt{N}}} \] is distributed according to a student-t distribution with $N-1$ degrees of freedom.
The rest of the test is exactly as we would perform the large-sample test, except that intead of using the CDF $\Phi(Z)$ of a standard normal RV, we will now use the CDF of a student-t with $N-1$ degrees of freedom. We will represent this as $P(Z \leq T) = t(T,N-1)$. In the description below we assume $\alpha_z$, the highest acceptable probability of type-1 error, has been specified.
Student-t table:To obtain CDF values for the student-t distribution, we must refer to a student-t table. Here is an excellent table provided by NIST. Note that the table is presented differently from the manner in which the CDF of normal RVs is presented. Here, the left most column represents the degrees of freedom. The top (header) row shows the CDF. The table entries themselves show the $T$ value at which this CDF is obtained. So, for example, the third column (corresponding to header value 0.975) in the fourth row is 2.776. This indicates that $t(2.776,4) = 0.975$. Since the student-t distribution is symmetric, This also means that $t(-2.776,4) = 1 - 0.975 = 0.025$.
Let us now look at the tests themselves.
Left-sided test: When the alternate hypothesis $H_a$ is that $\mu < \mu_0$, then we find the largest tabulated $T$ value for which $t(T,N-1) \leq \alpha_z$, i.e. we find $T_\alpha = \arg\max_T (t(T,N-1) \leq \alpha_z)$. If $Z \leq T_\alpha$ we reject the null hypothesis.
Consider our bulb example. If we suspect that $\mu < \mu_0$, our sample comprises 20 bulbs, and if we desire a confidence of 95%, i.e. $\alpha_z = 0.05$ in rejecting $H_0$, then we need a $T_\alpha$ value such that $t(T_\alpha, 19) = 0.05$. From the student-t table we find that $t(1.729,19) = 0.95$, from which we deduce that $t(-1.729,19) = 0.05$, so our $T_\alpha = -1.729$. If $Z \leq -1.729$, we can reject the null hypothesis.
Right-sided test: When the alternate hypothesis $H_a$ is that $\mu > \mu_0$, then we find the smallest tabulated $T$ value for which $t(T,N-1) \geq 1-\alpha_z$, i.e. we find $T_\alpha = \arg\min_T (t(T,N-1) \geq 1-\alpha_z)$. If $Z \geq T_\alpha$ we reject the null hypothesis.
In our bulb example, if we suspect that $\mu > \mu_0$, our sample comprises 20 bulb, and if we desire a confidence of 95%, i.e. $\alpha_z = 0.05$ in rejecting $H_0$, then we need a $T_\alpha$ value such that $t(T_\alpha, 19) = 0.95$. From the student-t table we find that $t(1.729,19) = 0.95$, so our $T_\alpha = 1.729$. If $Z \geq 1.729$, we can reject the null hypothesis.
Two-sided test: When the alternate hypothesis $H_a$ is simply that $\mu \neq \mu_0$, then we must verify that $|Z|$ exceeds a threshold that provides the necessary confidence in the test. To find the threshold we must find the smallest $T_{\frac{\alpha}{2}}$ from the student-t table such that $t(T_{\frac{\alpha}{2}}, N-1) \geq 1 - \frac{\alpha_z}{2}$. If $ |Z| \geq T_{\frac{\alpha}{2}}$, we can reject the null hypothesis.
In our bulb example, if we suspect simply that $\mu \neq \mu_0$, and $\alpha_z = 0.05$ as before, then we need a $T_\alpha$ value such that $t(T_\alpha, 19) = 0.025$. From the student-t table we find that $t(2.093,19) = 0.975$, so our $T_\alpha = 2.093$. If $|Z| \geq 2.093$, we can reject the null hypothesis.