Advanced BST Operations
Topics Discussed
Tree Traversals, Delete operation
(more examples) and AVL trees
Traversing Trees
One of the important operations on a BST is to find a way to traverse all the nodes in the tree. As we know traversing a linked list or array is easy. We just start from the first node and traverse linearly until we come to the end of the list. But, it is not so trivial in a BST. Consider the binary search tree
38
/ \
5 45
/ \ \
1 9 47
/ \ /
8 15 46
/
13
There are several methods of traversing trees. Among them are the inorder, preorder and postorder traversal of nodes. Each of these traversal algorithms visit every node of the BST in a particular order.
InOrderTraversal : The idea of inorder traversal is that we visit the nodes in the order left-root-right, meaning for any subtree in the path, left node must be visited first followed by root and right node.
- Left, Root, Right
- Prints the values in ascending order
In the above example, the in-order traversal is
1, 5, 8, 9, 13, 15, 38, 45, 46, 47
Inorder traversal is always symmetrical.
Implementation: The implementation of inorder traversal is fairly straightforward.
private void inorder(Node root){
if (root != null) {
inorder(root.leftChild);
// visit root;
inorder(root.rightChild);
}
PreOrderTraversal
- root, left, right
- processed as the node is visited
In the above example, the pre-order traversal is
38, 5, 1, 9, 8, 15, 13, 45, 47, 46
Imagine a car, which goes around a tree, starting with a root and keeping the tree on a left side.
PostOrderTraversal
- left, right, root
- node is not processed until the children are
In the above example, the post-order traversal is
1, 8, 13, 15, 9, 5, 46, 47, 45, 38
This picture demonstrates the order of node visitaion in postorder, preorder, and inorder traversals:

LevelOrderTraversal
- Processing nodes from top to bottom, left to right
In the above example, the level-order traversal is
38, 5, 45, 1, 9, 47, 8, 15, 46, 13
We can implement the level-order traversal using the API's LinkedList class.
There are number of other operations that can be performed on BSTs. Among them finding the height of a tree, depth of a node, counting the total nodes, computing the balance factor of a node is important.
Path from Node A to Node B
First we must define the notion of a path. We say there is a path from node A to node B if there is a (unique) way to get from A to B. The path length is defined as the number of edges in the path from A to B. Note that number of nodes is one more than the number of edges. The height of a tree is defined as the length of the longest path from root to any leaf node. Depth of a node is defined as the path length from root to node. The height of a node is defined as path length from node to the deepest leaf node in the tree.
Euler
The three common traversal algorithms can be represented as a single algorithm by assuming that we visit each node three times. An Euler tour is a walk around the perimeter of a binary tree where each edge is a wall, which you cannot cross. In this walk each node will be visited (touched) either on the left, or in the below, or on the right. For a left these three visits happen one right after the other, whereas for interior nodes that is not a case. The Euler tour in which we visit nodes on the left produces a preorder traversal. When we visit nodes from the below, we get an inorder traversal. And when we visit nodes on the right, we get a postorder traversal.
Exercise : Is it possible that the preorder traversal of a binary tree with more than one node visits the nodes in the same order as the postorder traversal?
Exercise: Draw a binary tree T such that : each node stores a single character , a preorder traversal of T yields BINARY, a postorder traversal of T yields NRYAIB
B
/
I
/ \
N A
/ \
R Y
Delete Operation
Algorithm: (two steps)
· 1. Find a node to be deleted (throw an exception otherwise)
· 2. Delete the node
Depending on where the node is found, we will consider three sub-cases: Deleting a leaf node, deleting a node with one child; and deleting an internal node( node with 2 children).
· node.left == null
- make a parent node point to a right child;
· node.right == null
- make a parent node point to a left child;
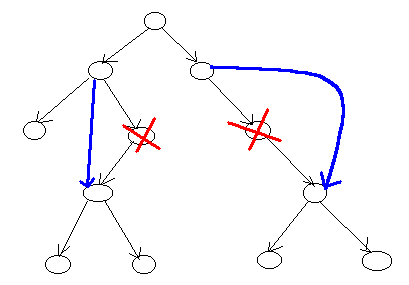
Deleting a Node with one child
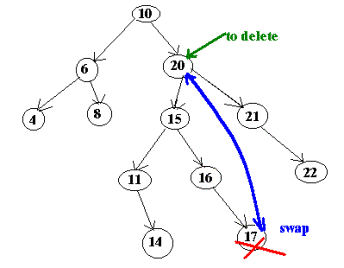
Deleting an internal Node

Deleting the root of the tree
Implementation (part I):
public void delete (Comparable d){root = deleteHelper(root, d);
}
private BNode deleteHelper (BNode r, Comparable d)
{ if (r == null)throw new RuntimeException("cannot delete.");
elseif (d.compareTo(r.data) < 0)
r.left = deleteHelper (r.left, d);
elseif (d.compareTo(r.data) > 0)
r.right = deleteHelper (r.right, d);
else { size--;if (r.left == null)
return r.right;
elseif (r.right == null)
return r.left;
else {// to be continued...
}
}
return r;}
Consider the binary search tree
38
/ \
5 45
/ \ \
1 9 47
/ \ /
8 15 46
/
13
and suppose we want to delete a node with the label 15. Here is a stack of recursive calls:
38.left = deleteHelper(5_node, 15)
5.right = deleteHelper(9_node, 15)
9.right = deleteHelper(15_node, 15)
deleteHelper(15_node, 15) returns 13_node
Because of the last two lines, the node 9 is be connected to 13, and the node 15 is deleted (since there is no references pointed to it).
· delete a node with TWO children
- find the rightmost node in the left subtree and
swap data between these two nodes.
The rightmost node will be the node with the greatest value in the left subtree. Why do we need this node? One way of thinking about it is that you want to replace the node to be deleted with a node that has the biggest value in the left subtree. Alternatively, you can swap data between the node to be deleted and the leftmost node in the right subtree.

Implementation (part II):
r.data = getNode(r.left).data; // swap data
where
private BNode getNode(BNode r)
{while (r.right != null) r = r.right;
return r;}
-Note.A node to be _actually_ deleted can have a left subtree:

To delete 15 you need to go to 9 and change the right reference to 15's left reference.
Implementation (part III):
r.left = getLink(r.left); //why do we need an assignment here??
where
private BNode getLink(BNode r)
{if (r.right != null)
r.right = getLink(r.right);
else r = r.left; return r;}
Answer: Consider a tree
38
/ \
5 45
in which you want to delete 38. On the first step you will move 5 to 38 node
5
/ \
5 45
On the second step you will need to remove the left subtree. If you do not do the assignment you will never set a left reference to null.
Exercise : If you delete a node from a BST and then insert it back, will you change the shape of the tree?
Traversing Trees using the Iterator class
Iterator
is the API interface. A class which implements Iterator
should implement three methods
booleanhasNext()- Returns true if the iteration has more elements.Object next()- Returns the next element in the iteration.voidremove()- (optional operation) Removes from the underlying collection the last element returned by next().
We implement a preorder traversal by ading a new
method iterator
to the BSTree class. This method returns an iterator over the nodes of a binary tree in pre-order:
public Iterator iterator()
{return new PreOrderIterator();
}
Class preOrderIterator
is an inner private class of BSTree. This class
implements the Iterator interface. We use the Stack
as an intermediate storage:
private class PreOrderIterator implements Iterator
{private Stack stk = new Stack();
// Construct the iterator.public PreOrderIterator()
{stk.push(root);
}
< ...skip...>
}
We
implement next()
public Object next(){BNode cur = (BNode) stk.peek();
if(cur.left != null)
{stk.push(cur.left);
}
else {//if a left child is null
BNode tmp = (BNode) stk.pop();while(tmp.right == null)
{if (stk.isEmpty()) return cur;
tmp = (BNode) stk.pop();
}
stk.push(tmp.right);
}
return cur;}
Algorithm - If there is a left child, we push the child on a stack and return a parent node. If there is no left child, we check for a right child. If there is a right child, we push the right child on a stack and return a parent node. If there is no right child, we move back up the tree (while-loop) until we find a node with a right child.
Here is a stack after returning 38 and 5:
| | cur | | | ||1 | <--- tmp | | | |
|5 | |5 |<--- tmp |9 |<--- tmp
|38| |38| |38|
---- ---- ----
We shall leave the method remove()
unimplemented. Since a binary tree has a nonlinear structure, removing a node
might cause the major tree rearrangement, which will lead to incorrect output
from next():
public void remove(){throw new java.lang.UnsupportedOperationException();
}
Balanced Trees
One strength of binary search trees (over other data structures) is its ability to maintain items in a way that search can be performed in O(log n)
Time, where n is the number of nodes. However this requires that we maintain the tree in a “balanced” form where entries are distributed evenly
among left and right sub trees of each node. Since most data sets in real life situations may come almost sorted or in some kind of order
(reverse sorted, already sorted). Therefore a naïve insertion into the tree may cause the tree to grow unbalanced. There are two ways to deal with
this situation. One option is to randomize the data before inserting to the tree. The cost of doing this operation is O(n). The drawback in this approach is that we need to know all the data in advance in order to randomize the set. Later when new data is inserted, we may not be able to apply the randomized algorithm again (unless we randomize the whole set). Therefore we need to think of ways to maintain a tree balanced (at low cost), when frequent insertions are performed.
AVL Trees
AVL trees, named after G. M. Adelson-Velskii and E. M. Landis were invented in 1962. The definition of an AVL tree is as follows. First we define the balanced factor of a node to be the absolute difference in heights of its left subtree and right subtree. For example, a given node with a left sub tree of height 4 and right sub tree of height 7 will have a balance factor of 3. We define an AVL tree to be a tree such that the balance factor of each node is
less or equal to 1.

In order to maintain a tree in AVL order, one must consider four cases. It is important to observe that when a new node is inserted into an AVL tree, a tree may become unbalanced as a result. Only the nodes in path of the tree will have their balanced conditions altered. So we need to consider few cases.
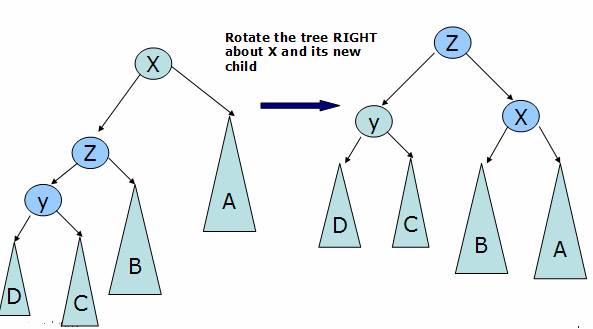
Case 1: The balance condition is violated for a node X by the left child of its left sub tree

In this case we rotate the tree right over x and fix the tree
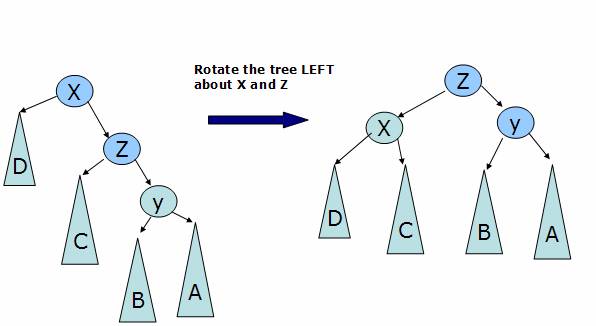
Case 2 : The balance condition is violated for a node X by the right child of its right sub tree

In this case we rotate the tree left over x and fix the tree
Case 3: The balance condition is violated for node X by the right child of the left sub tree. In this case we fix the tree by doing two operations

Next we do the following
Case 4: The balance condition is violated for node X by the left child of the right sub tree. In this case we fix the tree by doing two operations

And then we do the following
AVL trees are good data structures to maintain an “almost” balanced tree. However, AVL trees are no longer used in practice. For the most part
practical applications use other types of trees, in particular, “Splay Trees” (invented by CMU Professor Danny Sleator). Splay trees maintain access
to most frequently accessed elements by bringing them closer to the root. The discussion of splay trees is an appropriate topic for 15-211