15-212-X: Homework Assignment 2

Due Wednesday, September 24, 2:00 pm (electronically; papers at recitation.)

Maximum Points: 100

Guidelines

Strive for elegance in your code! Not every program which runs deserves full credit. Make sure to state invariants in comments which are sometimes implicit in the informal presentation of an exercise. If auxiliary functions are required, describe concisely what they implement. Do not reinvent wheels and try to make your functions small and easy to understand. Use tasteful layout and avoid longwinded and contorted code. None of the problems requires more than a few lines of SML code.
Make sure that your file compiles and runs. A program which doesn't run will not get full credit and is likely to incur a heavy penalty.
Homeworks must be all your own work.
Late homeworks will be accepted only until start lecture on Thursday, with a 25% penalty.
If you have any questions about the assignment, contact Matt Kraai at kraai@andrew.cmu.edu or use cmu.andrew.academic.15-212-X.discuss.

Please include the definitions from the file /afs/andrew/cmu.edu/scs/cs/15-212-X/assignments/ass2/ass2.sml in your solution file.

Problem 1: Shape Datatypes (30 pts)

In this exercise we investigate some of the data structures underlying drawing programs. If the drawing package has the primitives shapes circle and rectangle, and also allows groups of arbitrary shapes, we could use the following datatypes.

datatype Point = Pt of real * real;  (* The point (x,y) *)

datatype BareShape = 
    Circle of Point * real	(* Center and radius r, r >= 0 *)
  | Rectangle of Point * Point  (* Opposite corners *)
  | Group of BareShape list;    (* Group, non-empty *)

We do not enforce or expect any other invariants besides the stated ones. For example, a rectangle might degenerate to a line or point. Bare shapes are not general enough to represent information like color, area, or bounding boxes with each shape. To allow this kind of additional information, we generalize the above datatype of BareShape to be polymorphic.

datatype 'a Shape =
   Circle of Point * real * 'a      (* Center and radius, r >= 0 *)
 | Rectangle of Point * Point * 'a  (* Opposite corners *)
 | Group of ('a Shape) list * 'a;   (* Group, non-empty *)

Note that all shapes in a group must be annotated with information of the same type. A shape's bounding box is the smallest rectangle which encloses all points in the shape. The bounding box is always kept in canonical form (Pt(x1,y1), Pt(x2,y2)) where x₁ <= x₂ and y₁ <= y₂. Many operations for a drawing program can be implemented more efficiently if we store the shape's bounding box together with the shape. We therefore create a new type for bounding boxes, and an instance of 'a Shape where each shape has a bounding box, and possibly other information associated with it.

(* Box(Pt(x1,y1), Pt(x2,y2)) with x1 <= x2 and y1 <= y2 *)
datatype Box = Box of Point * Point;

type 'a BoxedShape = (Box * 'a) Shape;

Question 1.1 (20 pts)

Write a function which creates a shape with a bounding box from a shape, copying all other information which might be associated with a shape. The function should have the type

val boxShape : 'a Shape -> 'a BoxedShape

Make sure to organize your code into small functions and document each one of them.

Question 1.2 (10 pts)

You can use boxed shapes to speed up selecting an object on the screen. The core of picking an object is the function

val pointInShape : Point -> 'a BoxedShape -> bool

which returns true if the point is in the otherwise it returns false. Create a pointInShape function which uses bounding box information to quickly reject shapes which do not apply. Note that the function (pointInShape p) may return true for several overlapping objects.

Problem 2: Fibonacci Trees (40 pts)

Leonardo da Pisa, son of Bonacci, better known as Fibonacci ("Filius Bonaccii") is nowadays well-known mainly to mathematicians and computer scientists for the sequence of numbers that bear his name:

f₀ = 1

f₁ = 1

f_n+2 = f_n+1 + f_n

One of his major concerns in life (1180-1250) were however rabbits. In particular, he was interested in knowing how rabbits reproduce and, assuming to start with one male and one female rabbit, how many rabbits he would get after any fixed amount of time. For this purpose, he came up with the following (admittedly approximate) discrete model of rabbit reproduction:

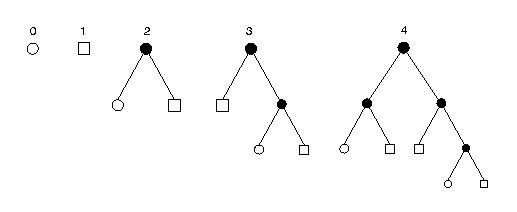
A couple of adult rabbits engenders another couple of rabbits every month;
it takes exactly one month for a young rabbit to become adult.

Starting from one couple of young rabbits, the evolution of the rabbit population can be represented by the infinite sequence of Fibonacci trees whose first five elements are as follows:

Couples of young rabbits are represented as empty circles, while adults are pictured as squares. Internal nodes contribute to the tree structure and can serve the purpose, for example, of computing the age of the rabbits.

The n-th element of this sequence, that we will denote as T_n, is a snapshot of the rabbit population at month n.

The following declaration describes the structure of Fibonacci trees

datatype fibTree = Young | Adult | Node of fibTree * fibTree

Note, however, that not every ML value of type fibTree has the form T_n.

Question 2.1 (10 pts)

Write an SML function nextFibTree, of type fibTree -> fibTree, that, given an object of type fibTree, expands its leaves according to Fibonacci's specification of rabbit reproduction, as exemplified in the figure above.

Note that your function should work for any value of type fibTree, not just for T_n.

Use nextFibTree to write a function createFibTree of type int -> fibTree that, given a natural number n, generates T_n.

Question 2.2 (15 pts)

One curious fact about Fibonnaci trees is that for any n, T_n+2 is a binary tree having T_n as its left subtree and T_n+1 as its right subtree. This is illustrated in the picture below.

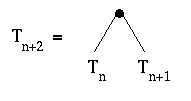On the basis of this property and of examples shown in class, devise an efficient implementation of the function createFibTree' performing the same task as the function createFibTree from the previous question. Carefully state and prove its correctness.

Question 2.3 (15 pts)

Write an SML function countLeaves, of type fibTree -> int, that returns the total number of leaves of a given tree (which may not be of the form T_n). Prove that countLeaves returns f_n when given the representation of T_n. Notice that this is the number of rabbit couples in the n^th month.

Problem 3: Rational Numbers (30 pts)

Standard ML does not contain a built-in library for operations on rational numbers. In this part of the assignment, you will create your own structure which provides many of the operations provided by the Standard ML Basis Library on reals and integers.

Implement a structure Rational which matches the signature RATIONAL.

Rationals should be stored as a pair of integers. In order to avoid unnecessary overflow, ensure that numerator and denominator have no common factors. Your functions should assume this invariant on their arguments and guarantee it for their results. Make sure to avoid unnecessary work.

All of the function results should be evident from their names (i.e., leq returns true if and only if its first argument is less than or equal to its second argument).

The fraction function should return the tuple of numerator and denominator, in reduced form. In case of a divide by zero, the divide function should raise the Div exception.

signature RATIONAL =
sig
  (* types *)
  type rational

  (* constants *)
  val zero : rational
  val one : rational

  (* conversions *)
  val rational : int * int -> rational
  val real : rational -> real
  val fraction : rational -> int * int

  (* operations *)
  val plus : rational * rational -> rational
  val minus : rational * rational -> rational
  val times : rational * rational -> rational
  val divide : rational * rational -> rational (* may raise exception Div *)

  (* relations *)
  val equal : rational * rational -> bool
  val leq : rational * rational -> bool
end;

Handin instructions

Put your SML code into a file named ass2.sml in your ass2 directory. All of your definitions should be in this one file. Your handin directory is

/afs/andrew/scs/cs/15-212-X/studentdir/<your andrew id>/ass2

Hand in your proofs for Questions 2.2 and 2.3 on paper at recitation.

last modified: Mon Sep 8 14:32:43 1997