Repulsive Curves
ACM Transactions on Graphics 2021
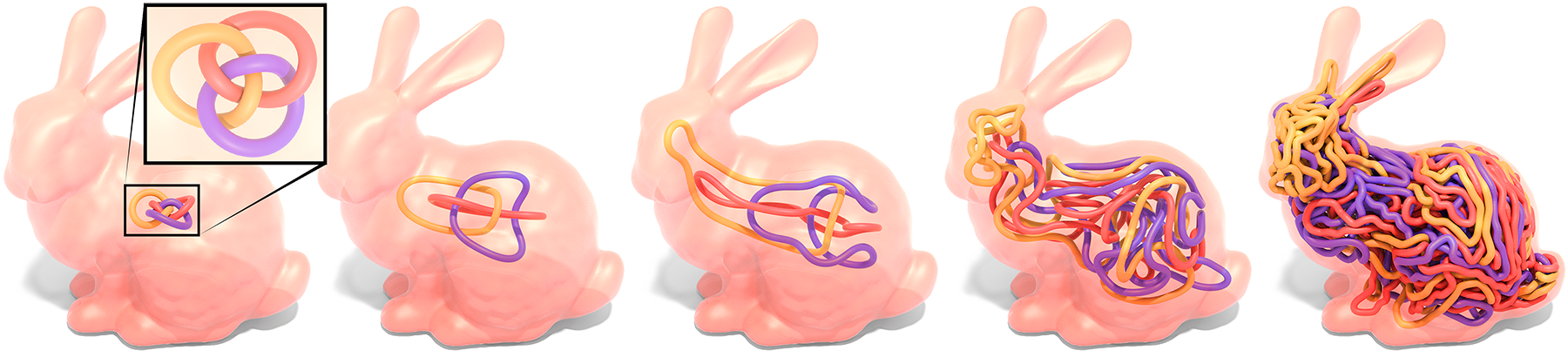
Curves play a fundamental role across computer graphics, physical simulation, and mathematical visualization, yet most tools for curve design do nothing to prevent crossings or self-intersections. This paper develops efficient algorithms for (self-)repulsion of plane and space curves that are well-suited to problems in computational design. Our starting point is the so-called tangent-point energy, which provides an infinite barrier to self-intersection. In contrast to local collision detection strategies used in, e.g., physical simulation, this energy considers interactions between all pairs of points, and is hence useful for global shape optimization: local minima tend to be aesthetically pleasing, physically valid, and nicely distributed in space. A reformulation of gradient descent, based on a Sobolev-Slobodeckij inner product enables us to make rapid progress toward local minima—independent of curve resolution. We also develop a hierarchical multigrid scheme that significantly reduces the per-step cost of optimization. The energy is easily integrated with a variety of constraints and penalties (e.g., inextensibility, or obstacle avoidance), which we use for applications including curve packing, knot untangling, graph embedding, non-crossing spline interpolation, flow visualization, and robotic path planning.
Video
|
This archive contains two datasets: Knot128 and Trefoil100. Both datasets are “stress tests” for knot untangling algorithms, i.e., highly-tangled configurations that can be difficult to smooth out into a canonical knot embedding. Knot128 is comprised of knots from 128 different isotopy classes; for each class we provide a tangled embedding, and a canonical embedding (for reference). Trefoil100 contains 100 tangled embeddings of the trefoil knot. To date, no algorithm—including ours—succeeds at untangling 100% of these knots (see paper/supplemental for statistics), though we get pretty close!
|
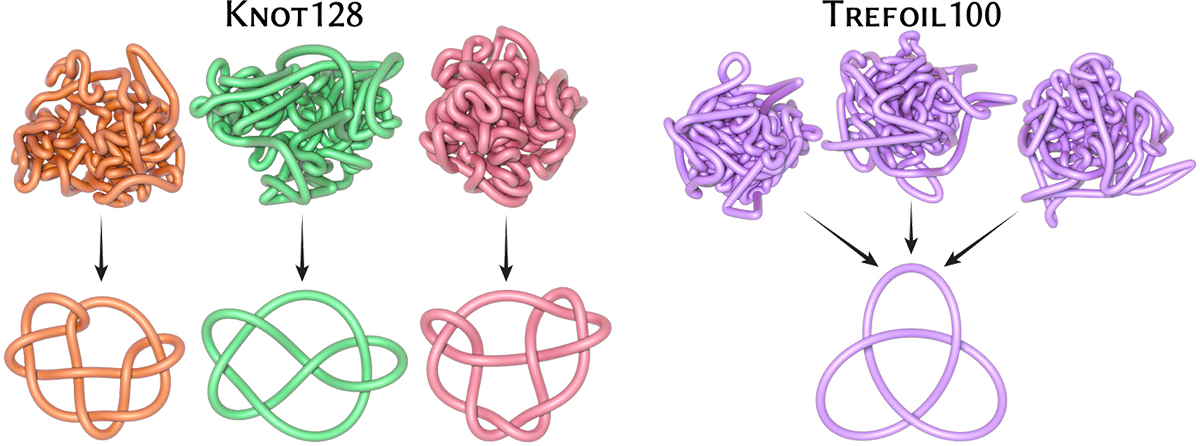
ZIP, 9.3MB
|
repulsive-curves—C++ implementation, with interactive visualization via Polyscope. Curves and constraints can be specified by a simple "scene file," which is solved to produce a sequence of optimized curves. Scenes support a wide variety of constraints and objectives, as described here.
Thanks to Stelian Coros for early discussion of these ideas. The bunny mesh is used courtesy of the Stanford Computer Graphics Laboratory. This work was supported by a Packard Fellowship, NSF awards 1717320 and 1943123, and gifts from Autodesk, Adobe, Activision Blizzard, Disney, and Facebook. The second author was supported by a postdoctoral fellowship of the German Academic Exchange Service (DAAD) and by the German Research Foundation (DFG) under project 282535003: Geometric curvature functionals: energy landscape and discrete methods. The third author was also supported by NSF award DMS-1439786 and Sloan award G-2019-11406 while in residence at ICERM.
@article{Yu:2021:RC,
author = {Yu, Chris and Schumacher, Henrik and Crane, Keenan},
title = {Repulsive Curves},
journal = {ACM Trans. Graph.},
volume = {40},
number = {2},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
Supplemental
Supplemental Material — We performed extensive comparison with 19 alternative preconditioning and optimization methods, finding that in general the fractional Sobolev scheme works significantly better than state-of-the-art optimization schemes for geometric energies. This document also details how we generated our knot dataset.
|
This archive contains meshes (at several resolutions) of the unknot from the paper “Möbius Energy of Knots and Unknots” by Freedman, He, and Wang, which is used as a performance benchmark in our paper.
|
ZIP, 1.8MB
|
Figures
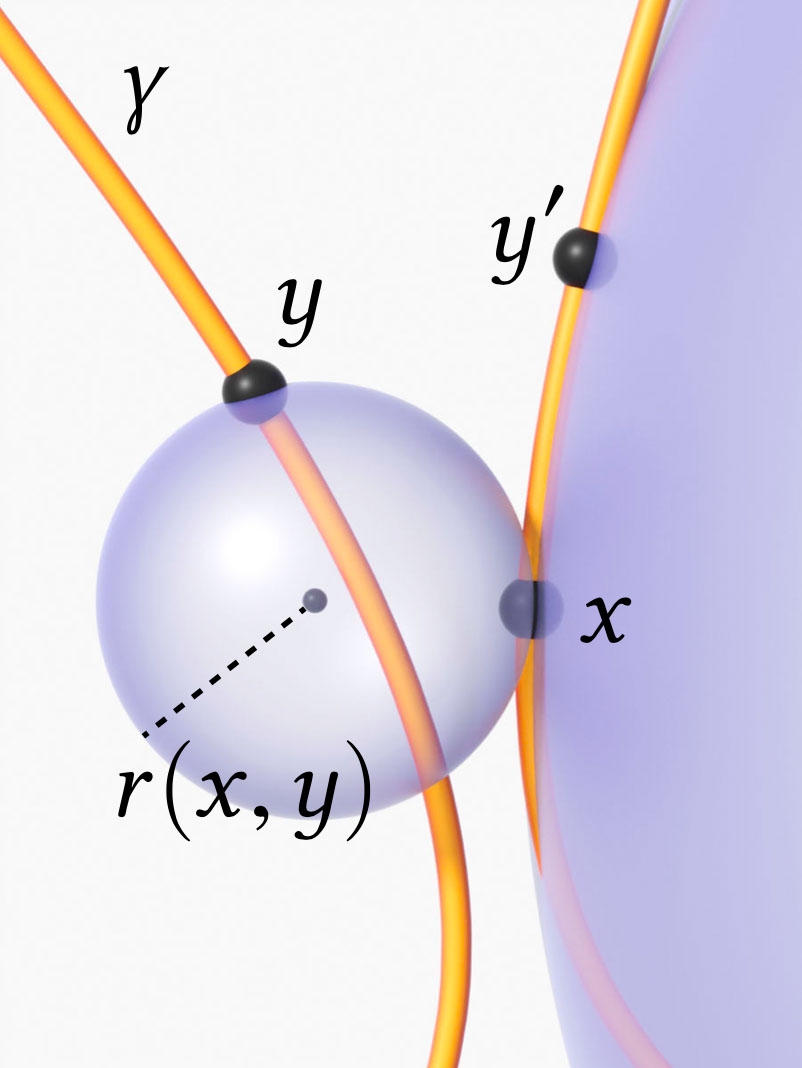
Our starting point is the tangent-point energy of Buck & Orloff (1995), which for each pair of points x and y on a curve considers the radius r of the smallest sphere tangent to x and passing through y. By penalizing the reciprocal of the radius 1/r(x,y), the energy provides an infinite barrier to collisions—while naturally ignoring points that are close in space merely because they are close along the curve itself.

Untangling the highly tangled Freedman unknot (top left) to the unit circle. For the same wall clock time, standard L2 gradient descent makes almost no progress, whereas conventional Sobolev descent fails to smooth out low (H1) or high (H2) frequencies. By carefully matching the inner product to the energy, our fractional Hs descent quickly flows to the circle.
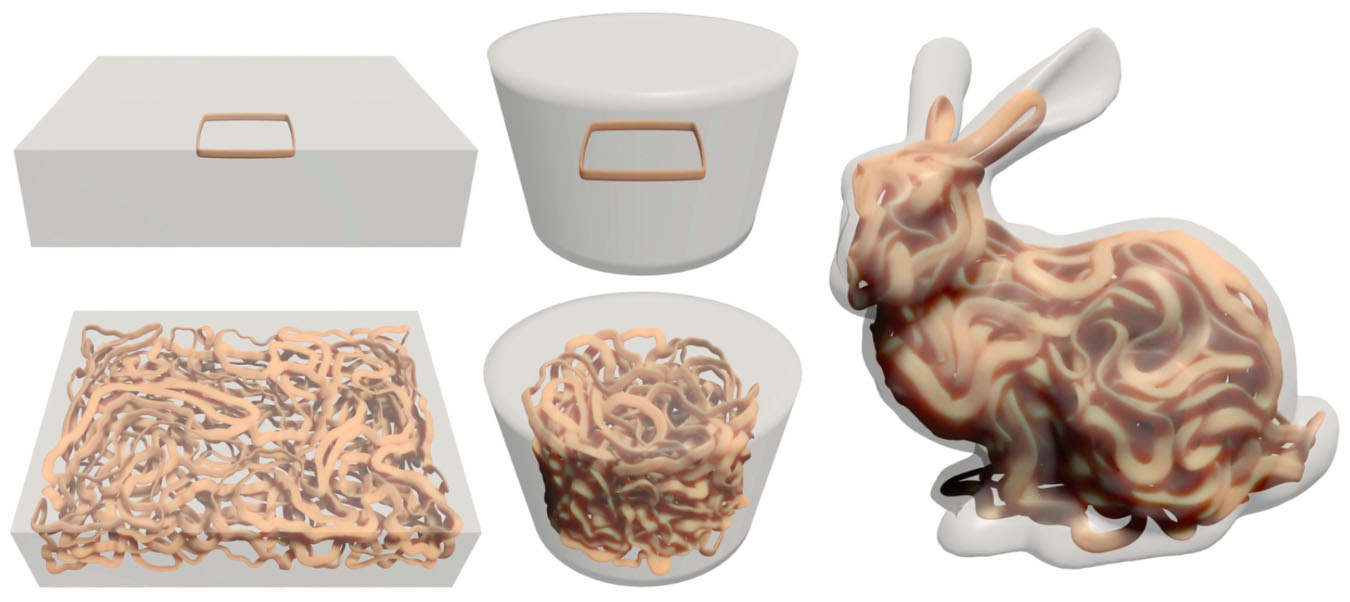
We can pack curves into a domain by penalizing their proximity to its boundary, and progressively increasing edge length. (Here we render curves with a non-circular cross section, which is not modeled by the energy.)

Patterns obtained by constraining a collection of repulsive curves to a surface and increasing their lengths (initial states shown above their final configurations).
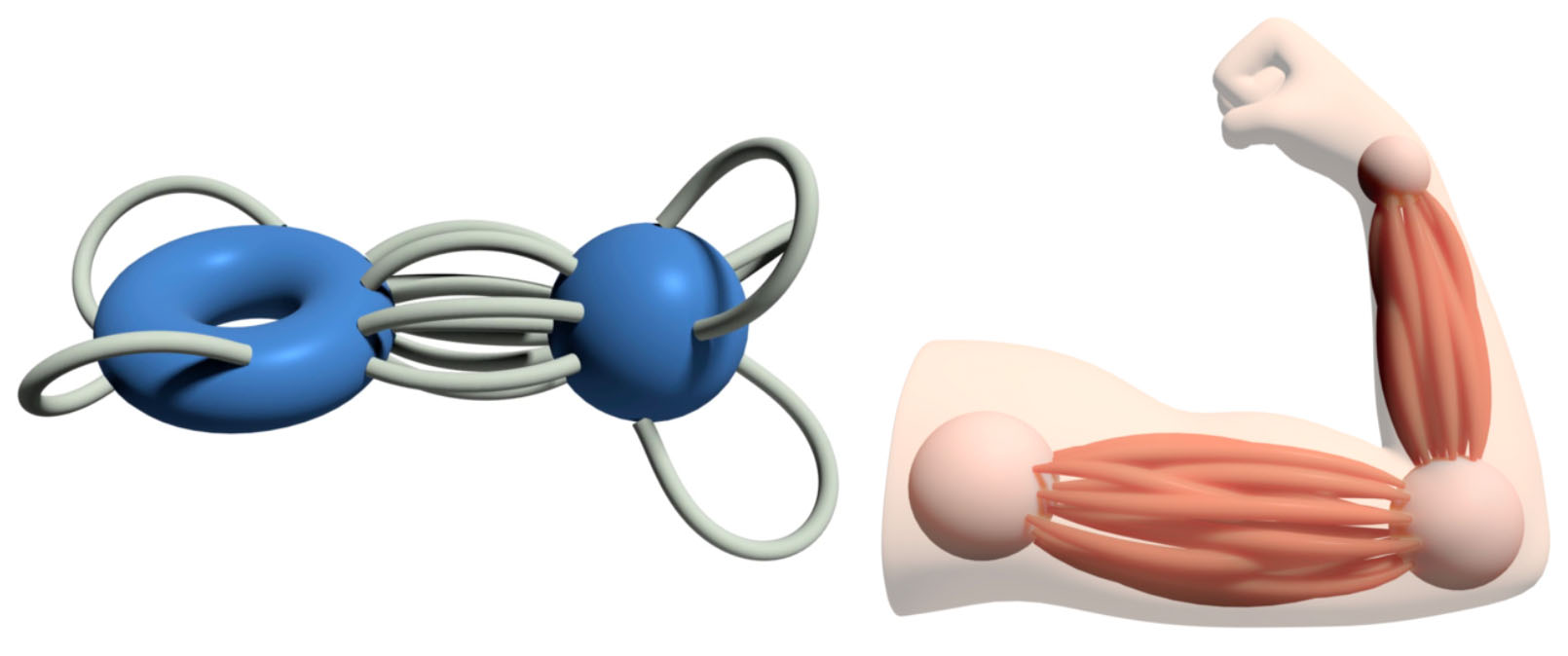
Allowing curve endpoints to slide freely over constraint surfaces (left) enables design tasks like arranging networks of muscles or muscle fibers (right).
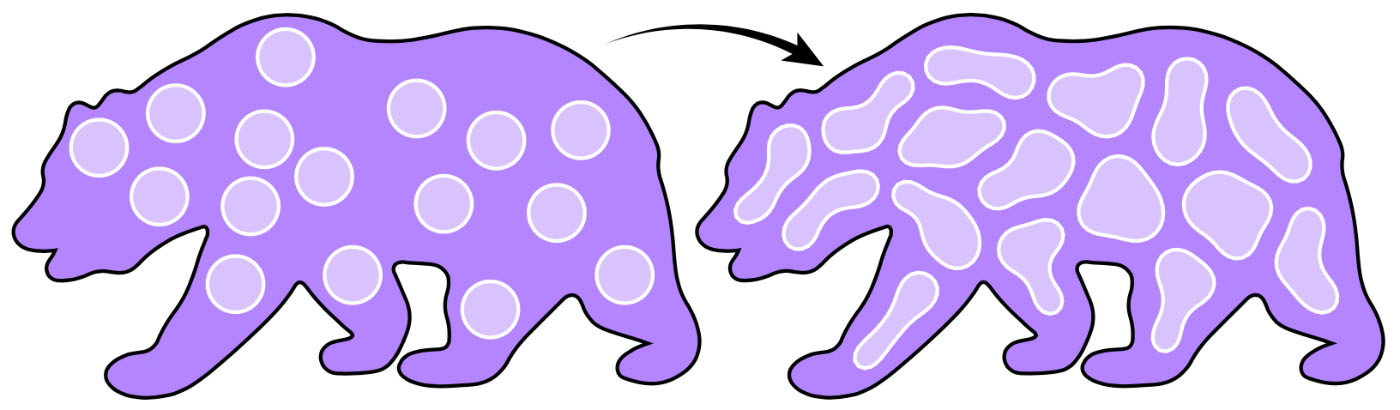
Just as repulsive potentials are used to equally-distribute points, we can compute collections of equally-spaced curves (here constrained to a region via a fixed curve potential).
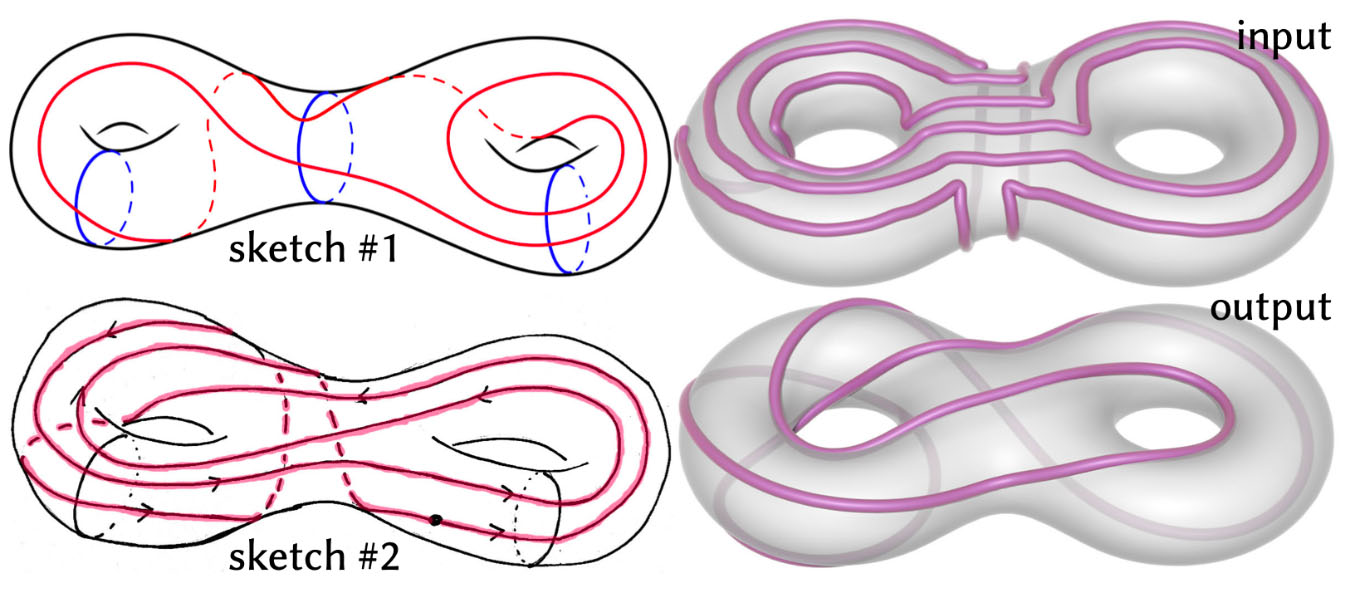
Topologically intricate loops can be difficult to draw by hand---the sketches at left (drawn by Nathan Dunfield) illustrate Dehn-Thurston coordinates. At right we generate an equispaced version of this curve by flowing a rough sketch, subject to an implicit surface constraint.
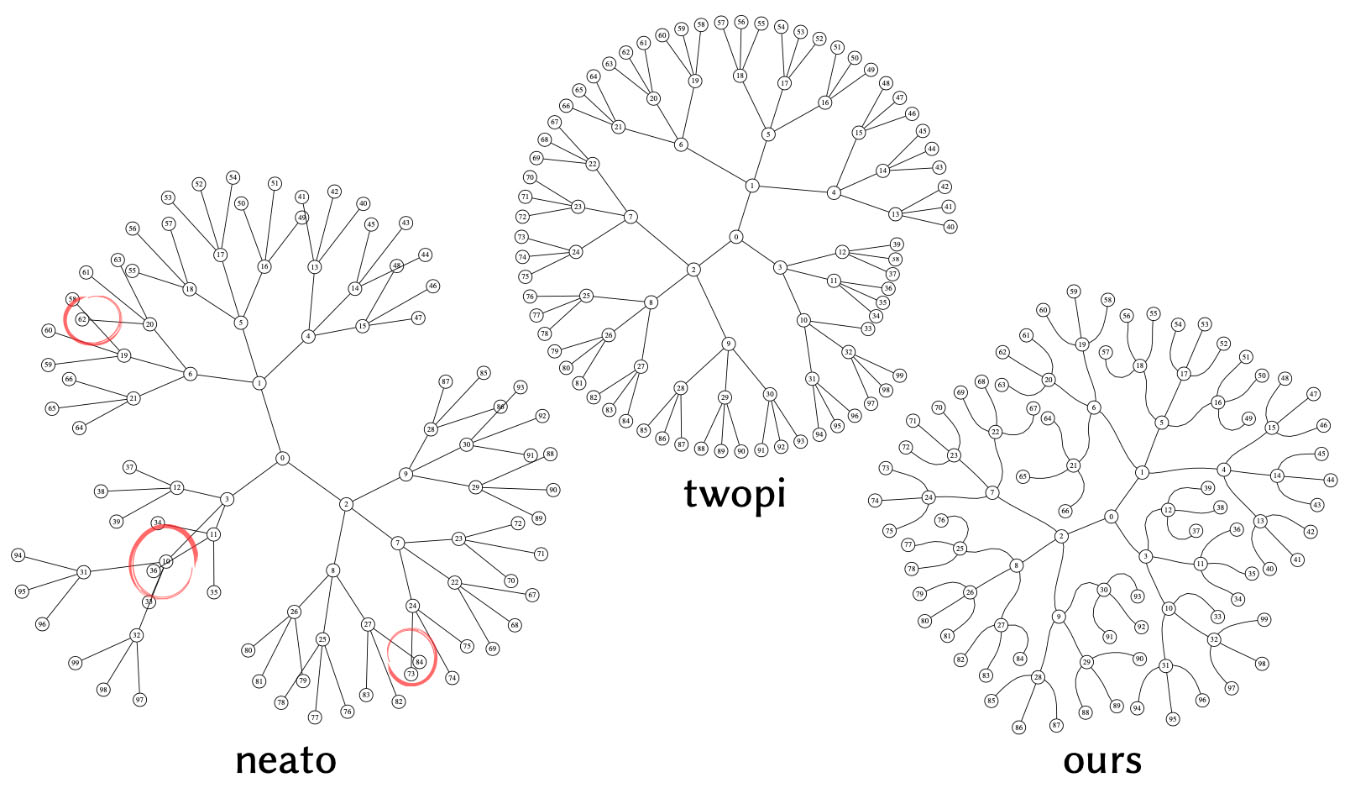
Traditional 2D graph drawing algorithms based on nodal proximity may cause edges to cross (left) or position nodes extremely close together (center); these layouts were produced by the popular Graphviz library. By treating edges as repulsive curves, we can obtain graph drawings that are both more compact and more legible (right).
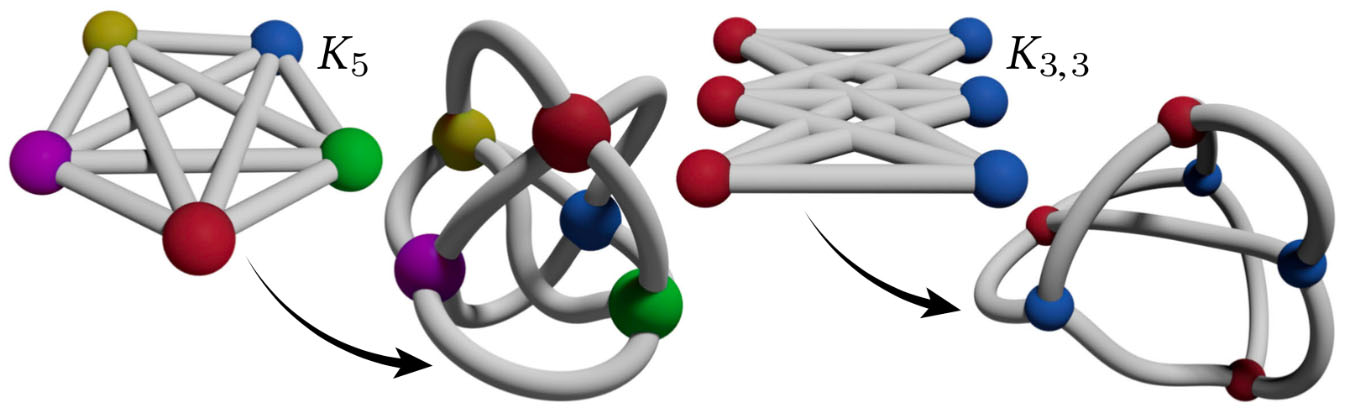
Isometric embedding: by jittering 2D drawings of non-planar graphs (which necessarily have crossings), curve repulsion with length constraints yields nicely spaced embeddings in R3 with prescribed edge lengths.
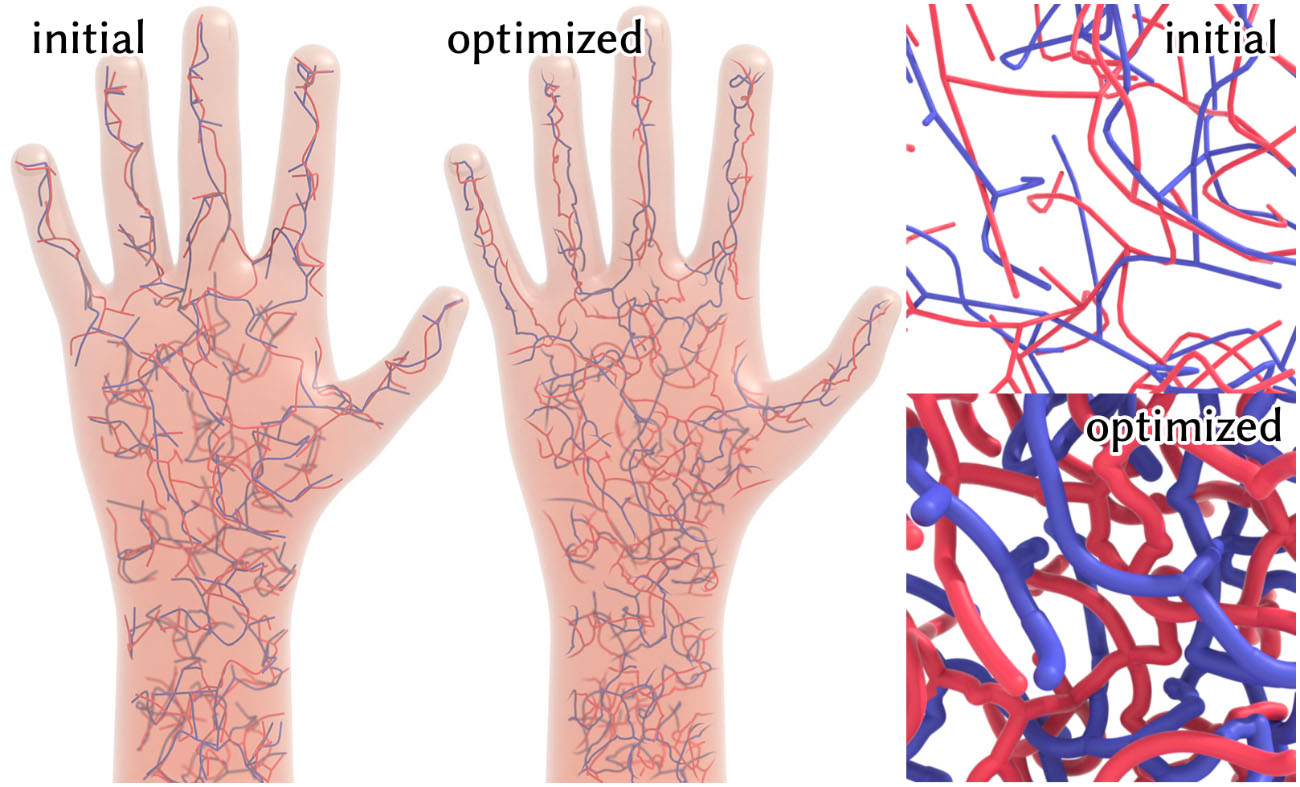
Left: a crude initial topology for a synthetic vascular network is optimized to achieve more uniform delivery of nutrients throughout a volume. Right: plotting the maximum collision-free thickness helps to visualize the improvement in uniformity.

As with Bézier curves, we can also control curve tangents at both interior and endpoints. Here we flow a polygonal curve (left), to a smooth interpolant with fixed points (red), and fixed points and tangents (blue).

Standard curve interpolation methods in 2D drawing programs can cause curves to self-intersect (center), even when the control polygon (left) does not. By starting from the control polygon and constraining the control points, we obtain a smooth, non-intersecting interpolant (right).
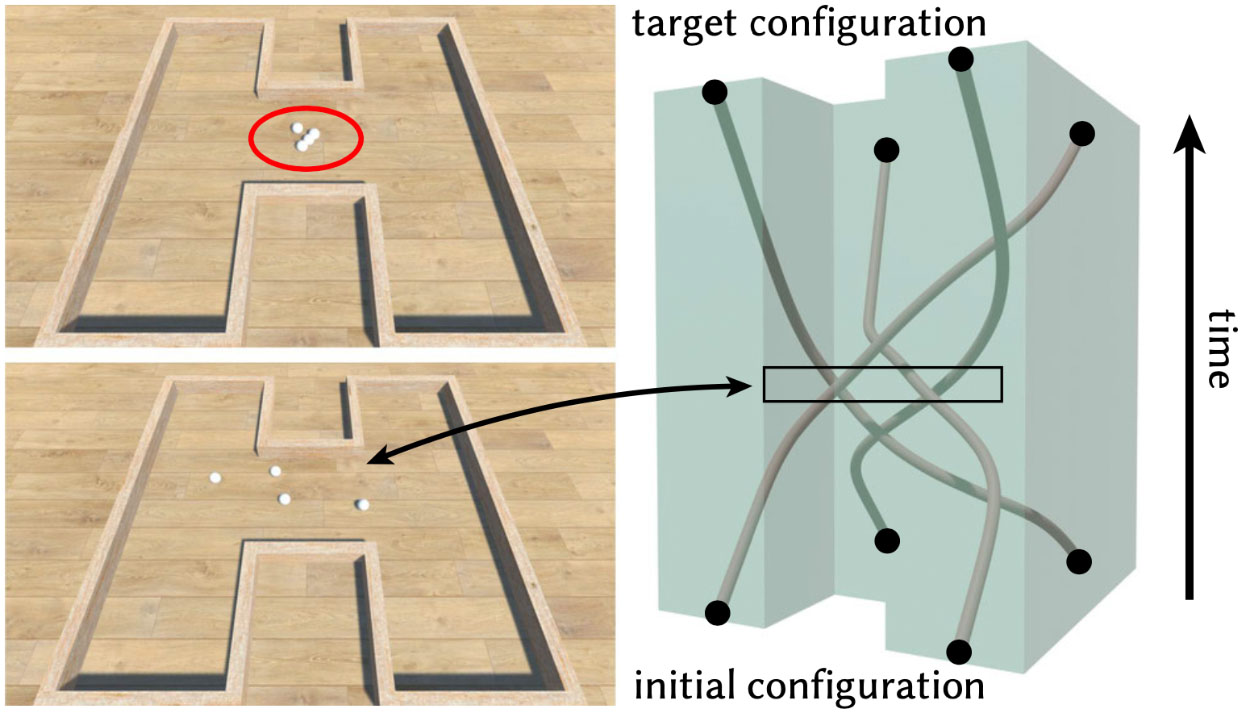
Top-left: In this path planning scenario, an initial trajectory brings the four agents dangerously close together. Bottom-left: By treating trajectories as curves in space-time, our system provides solutions that maximally avoid collisions, making them more robust to control errors. Right: Finding 2D trajectories is equivalent to optimizing a 3D braid with fixed endpoints constrained to an extrusion of the given environment. This same construction can easily be generalized to 3D environments.
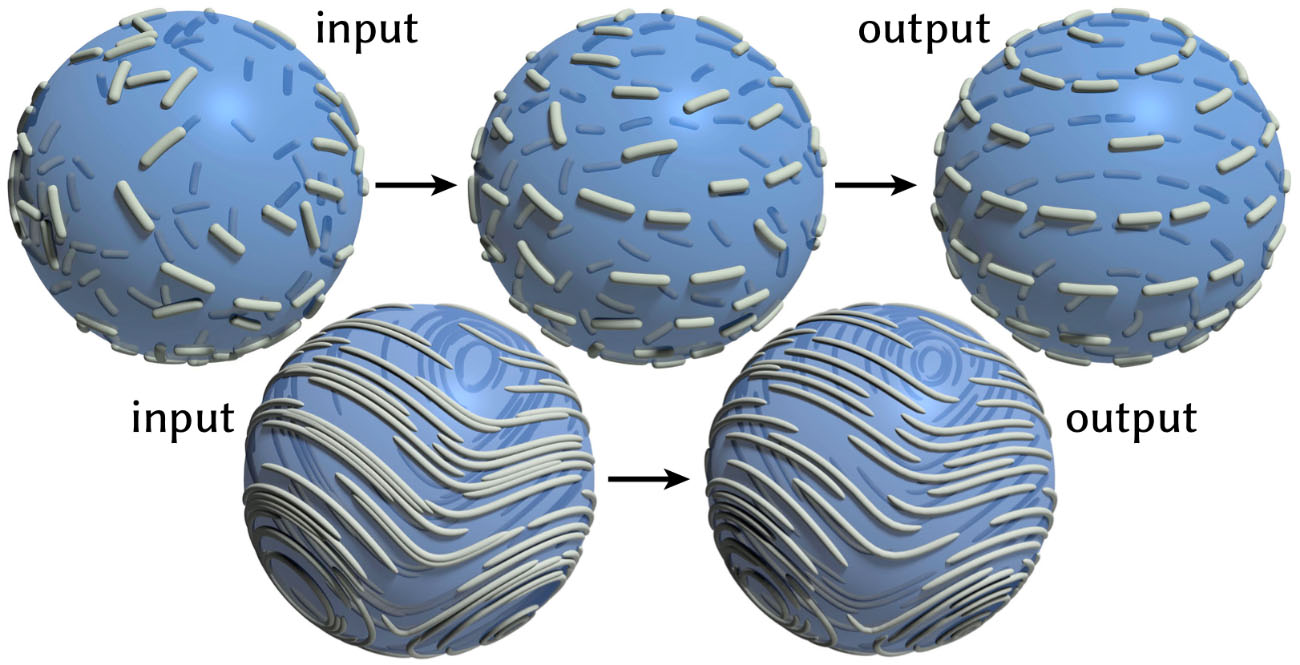
Encouraging curve tangents to align with a given vector field improve the quality of streamline visualization. Here, a random set of curve segments (top) aligns itself with a rotational vector field; we can also optimize randomly sampled streamlines (bottom) to improve their spacing.

Untangling a pair of earbuds via repulsion (see supplemental video).

Local minimizers of the tangent-point energy E2α. When α = 2 the tangent-point energy is scale-invariant and can exhibit “tight spots”; for larger values of α local interactions are penalized more than distant ones.
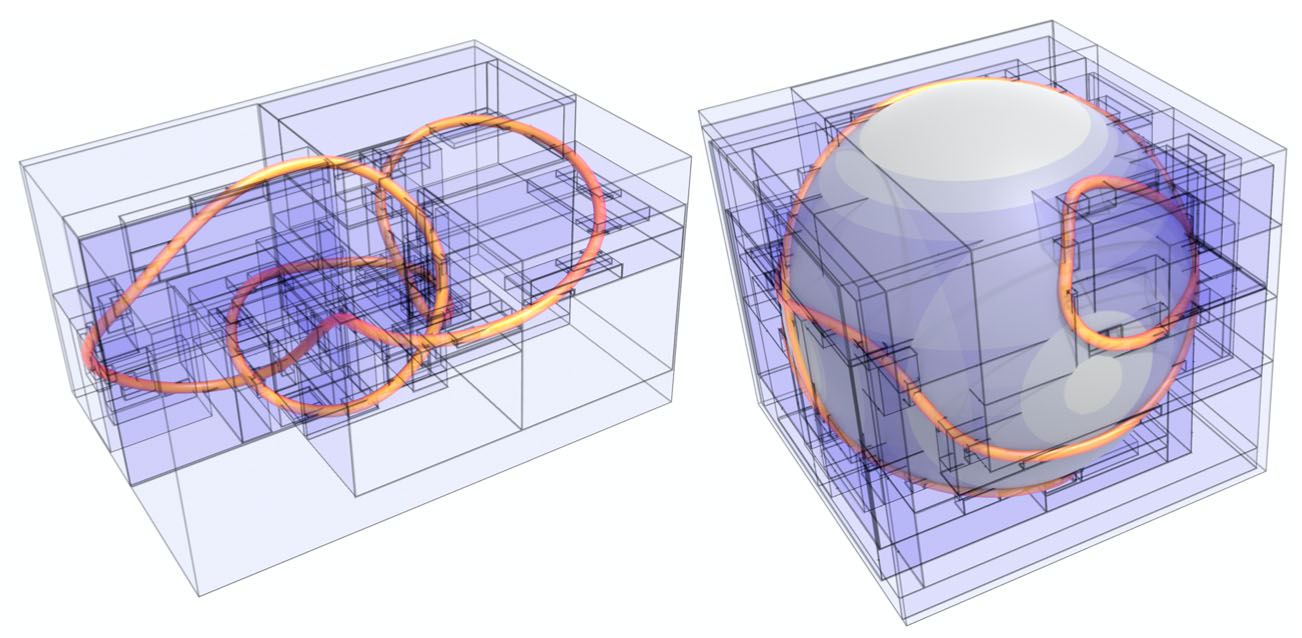
To accelerate evaluation of the tangent-point energy, we build a bounding volume hierarchy that partitions both positions (left) and tangent directions (right), here drawn as a curve on the unit sphere.
