Keenan Crane - Repulsive Shells

Repulsive Shells

ACM Transactions on Graphics 2024

Best Paper Award

Josua Sassen	Henrik Schumacher	Martin Rumpf	Keenan Crane
University of Bonn and École Normale Supérieure Paris-Saclay	Chemnitz University of Technology	University of Bonn	Carnegie Mellon University

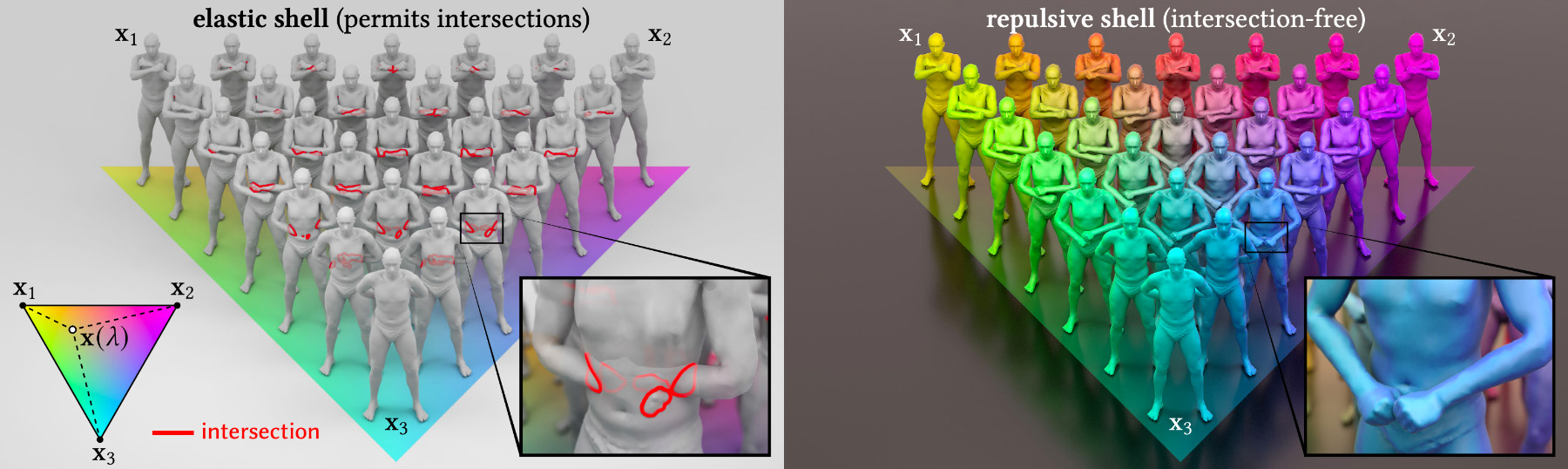
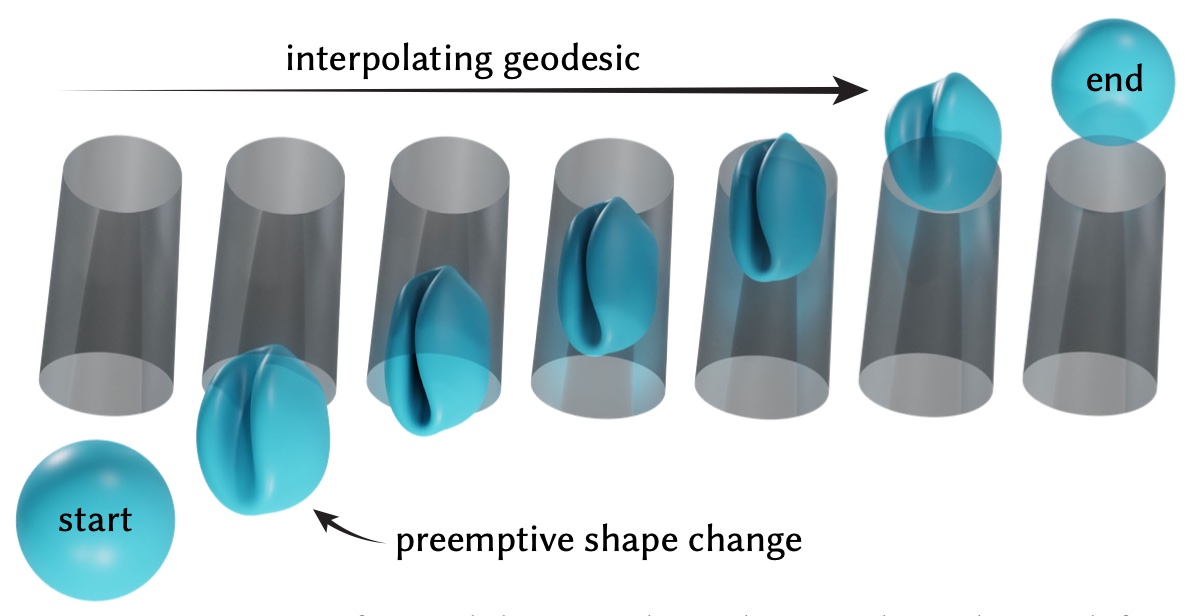
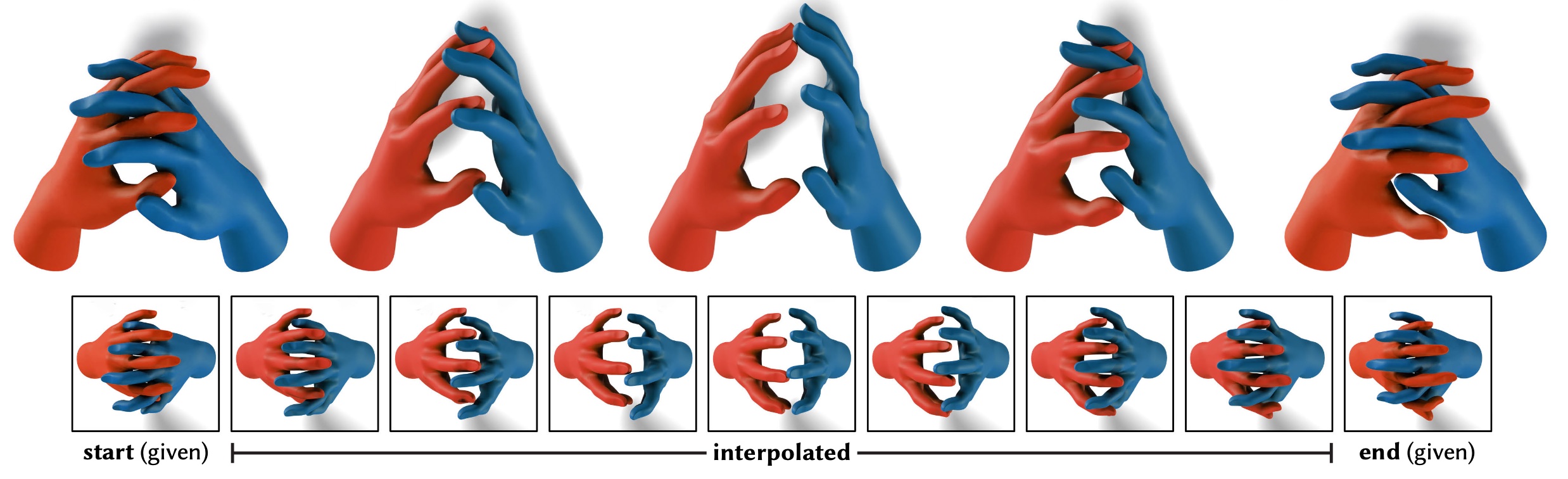
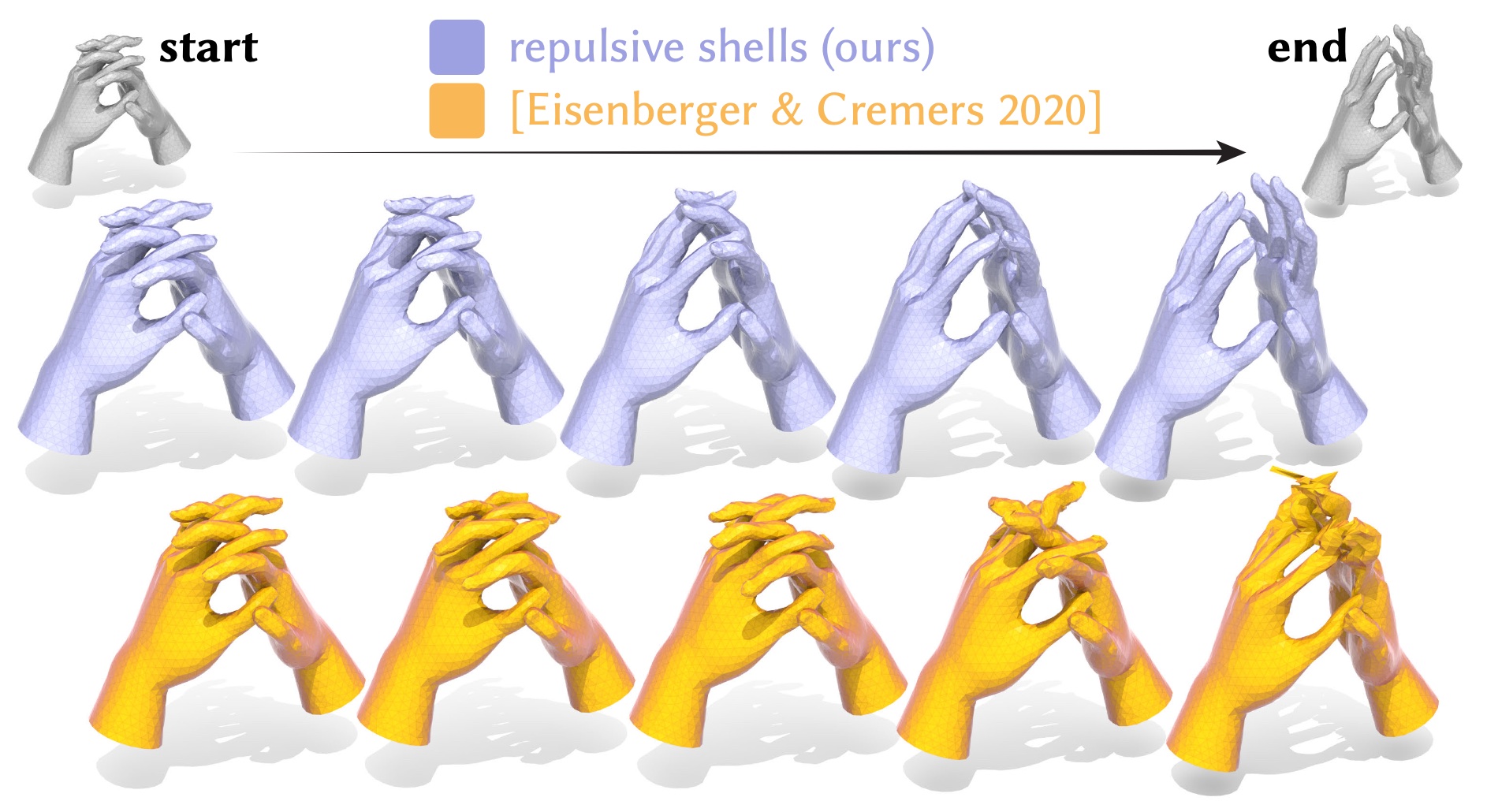
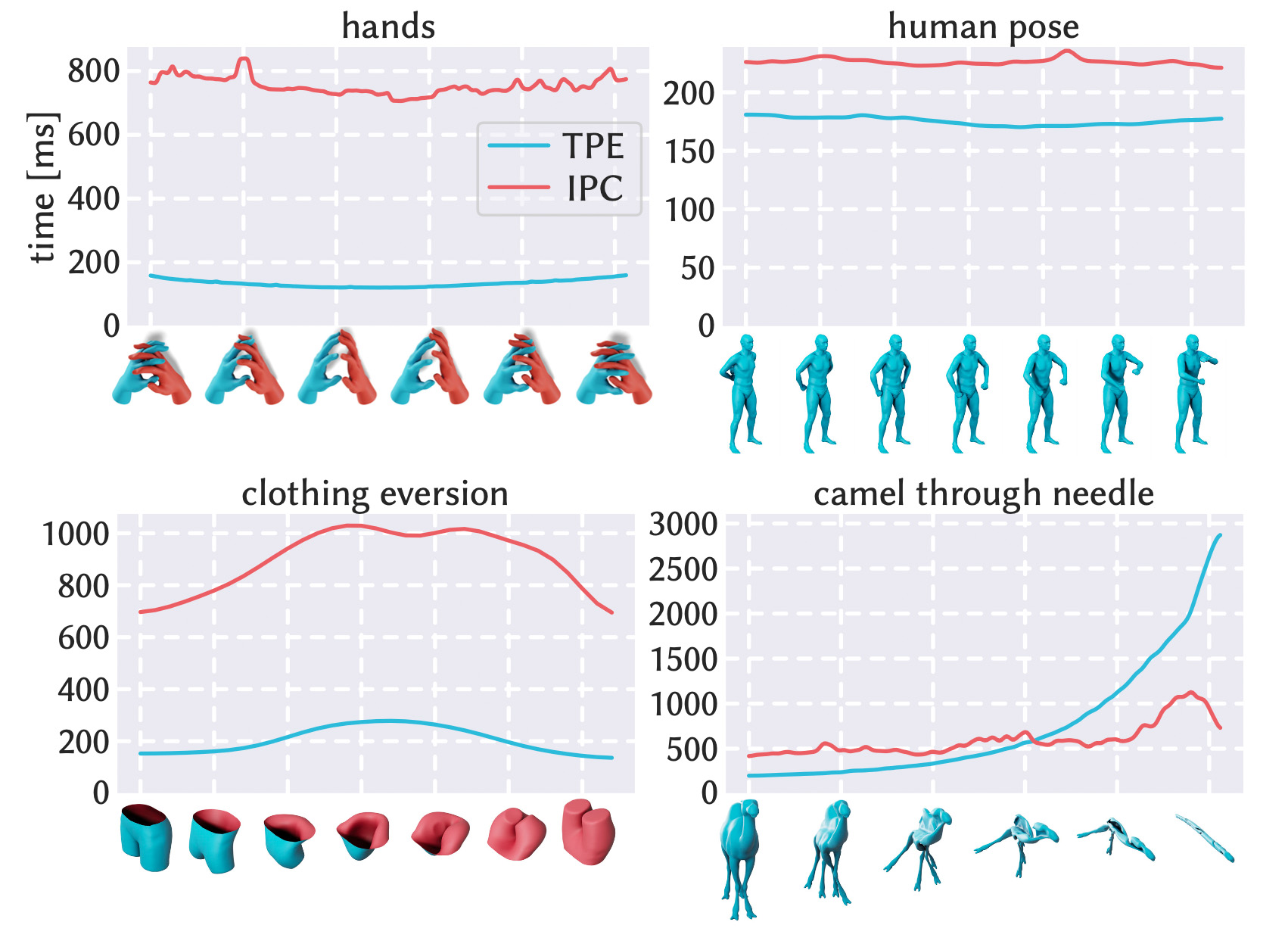
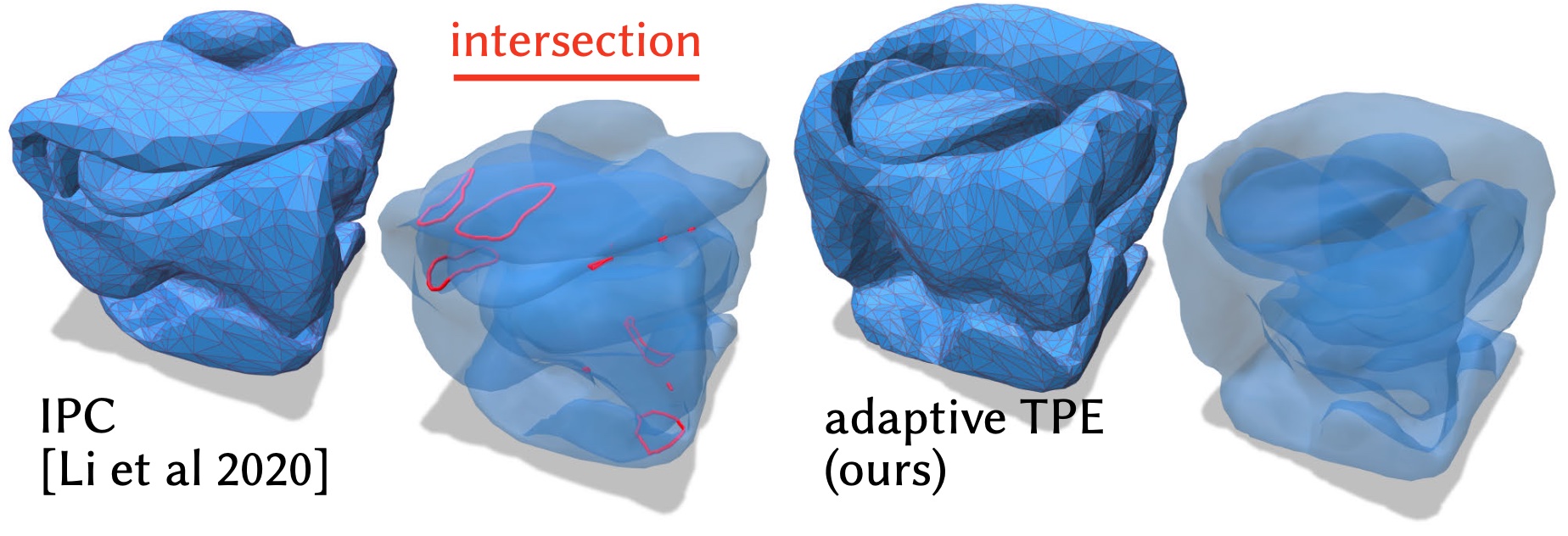
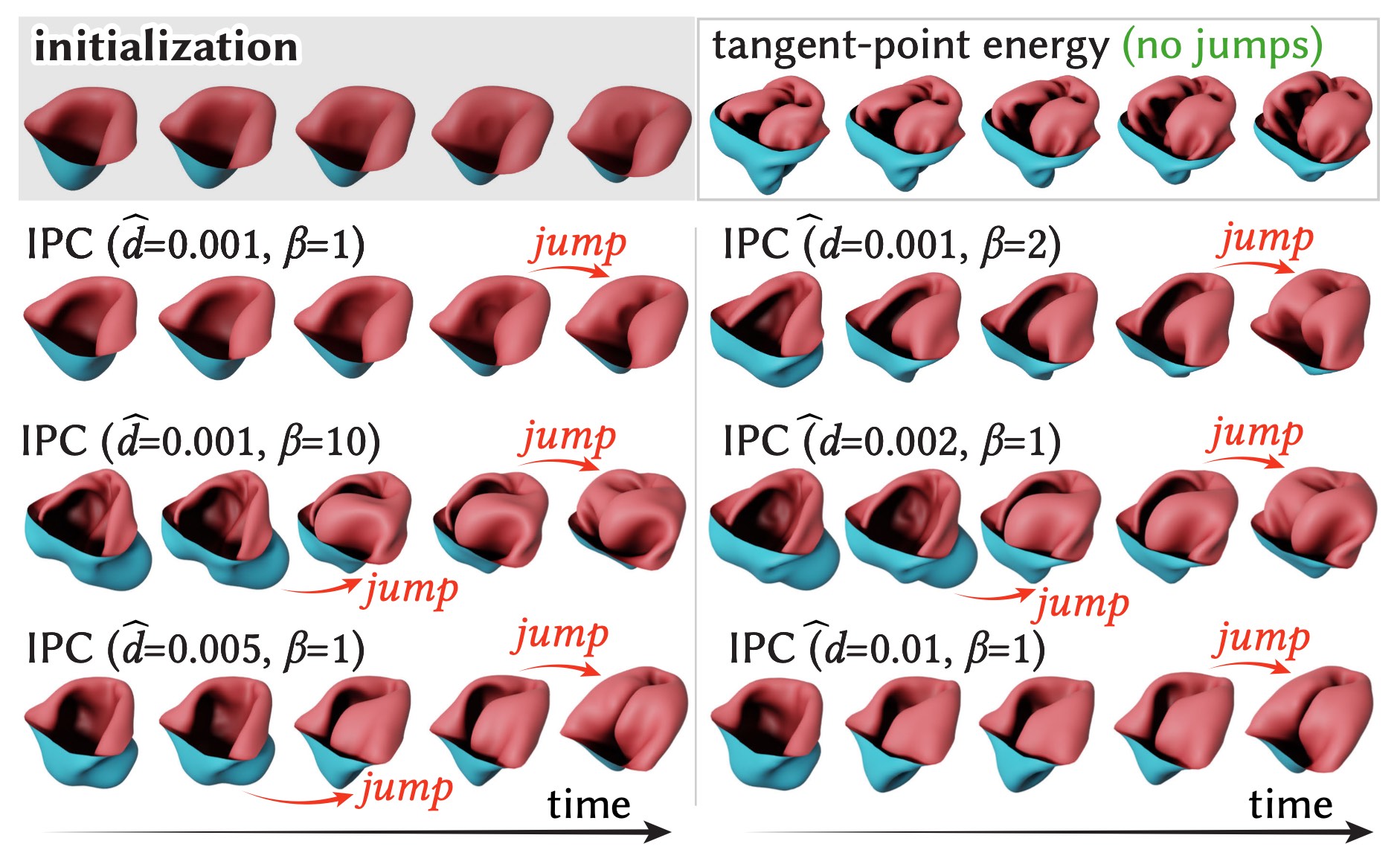
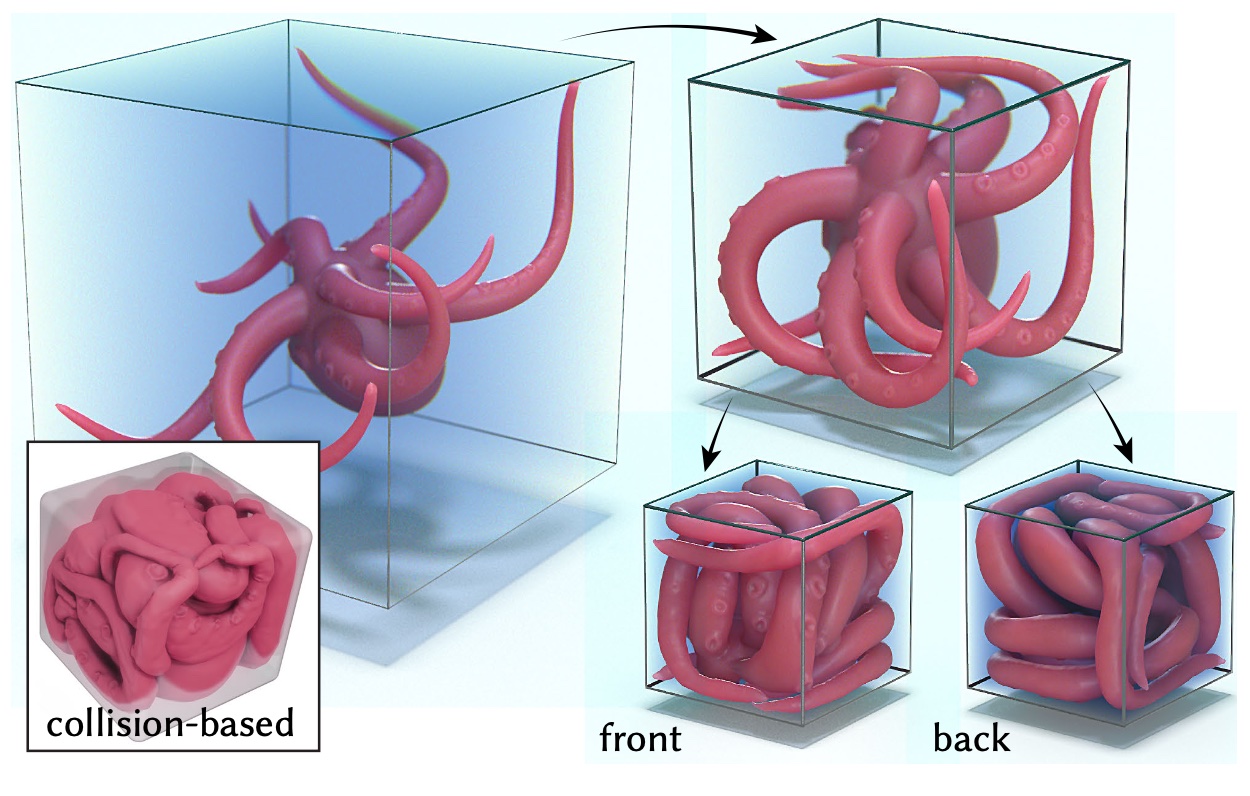
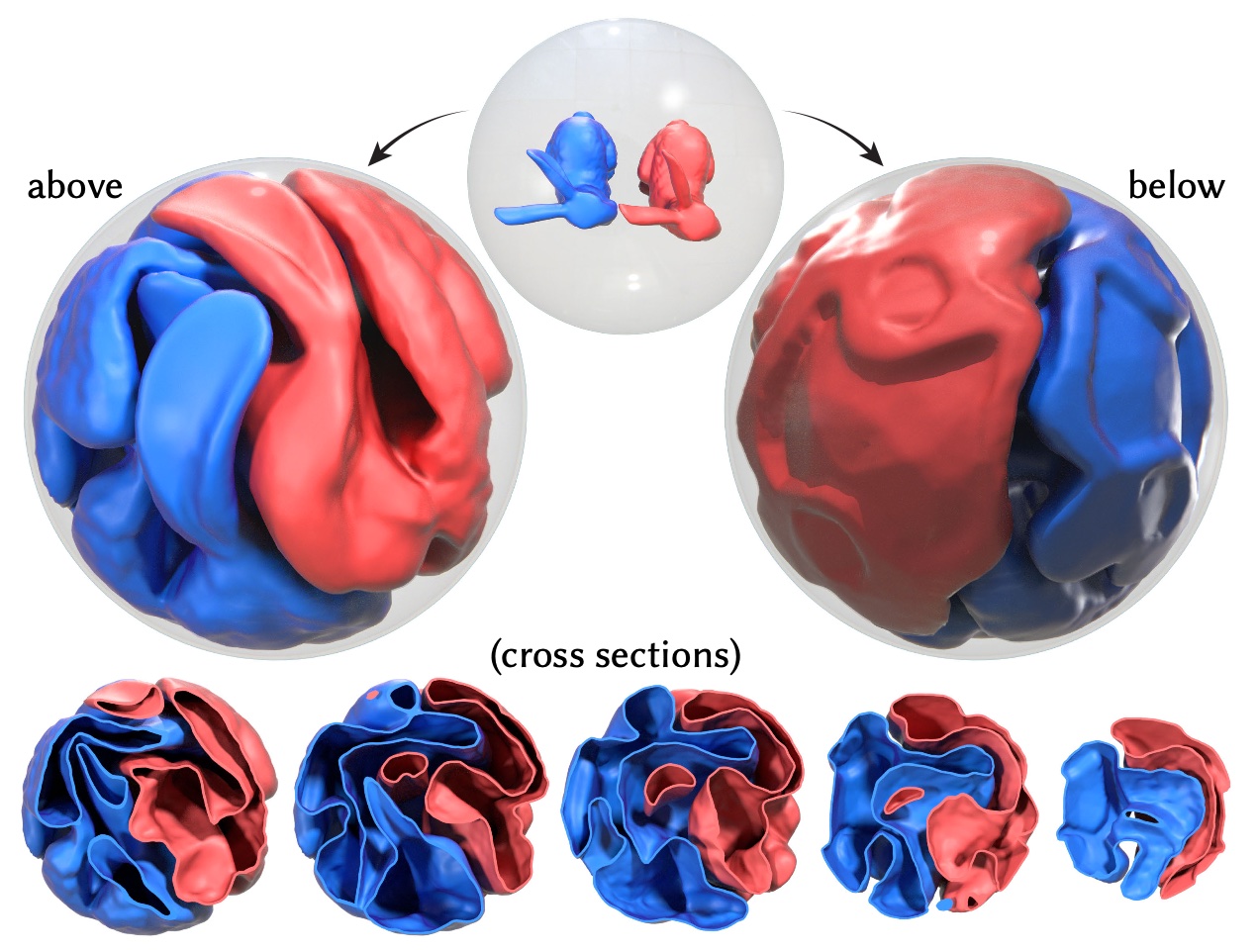
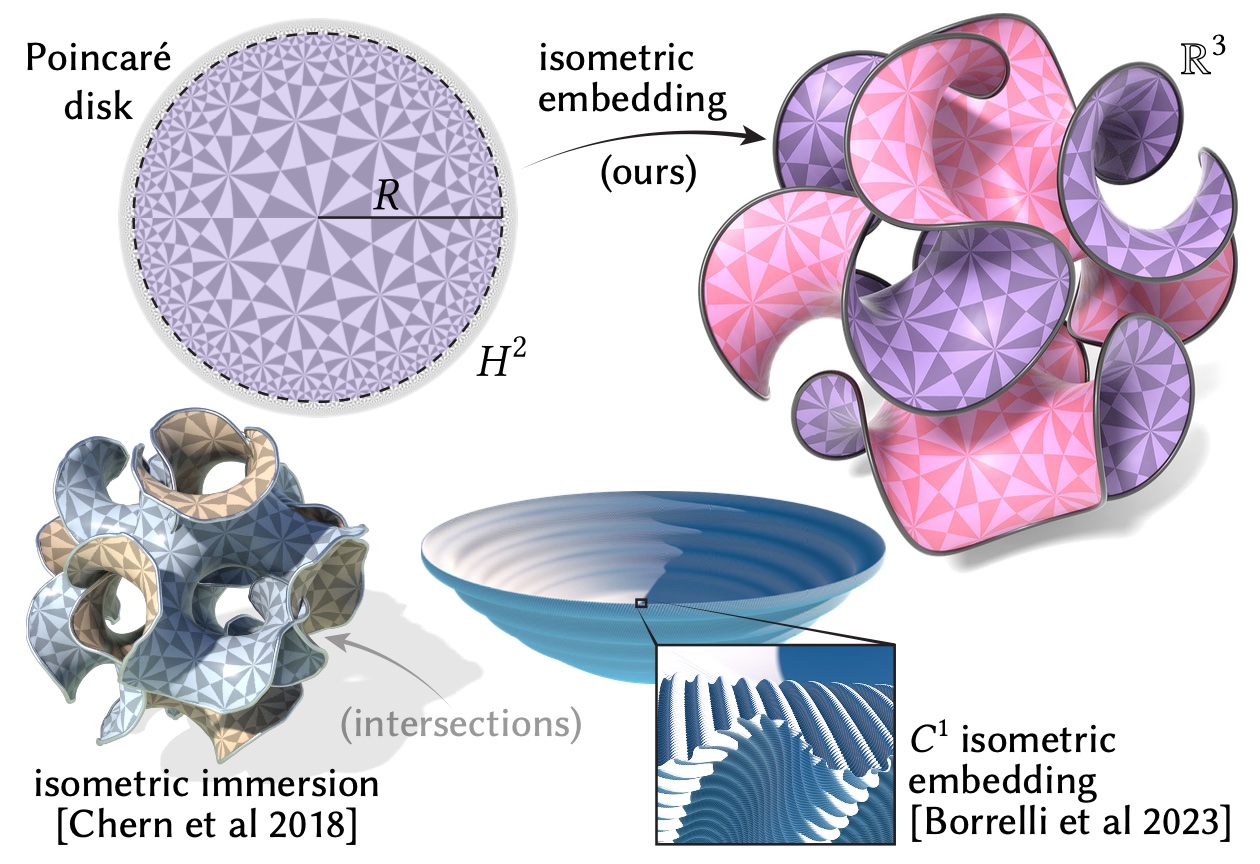
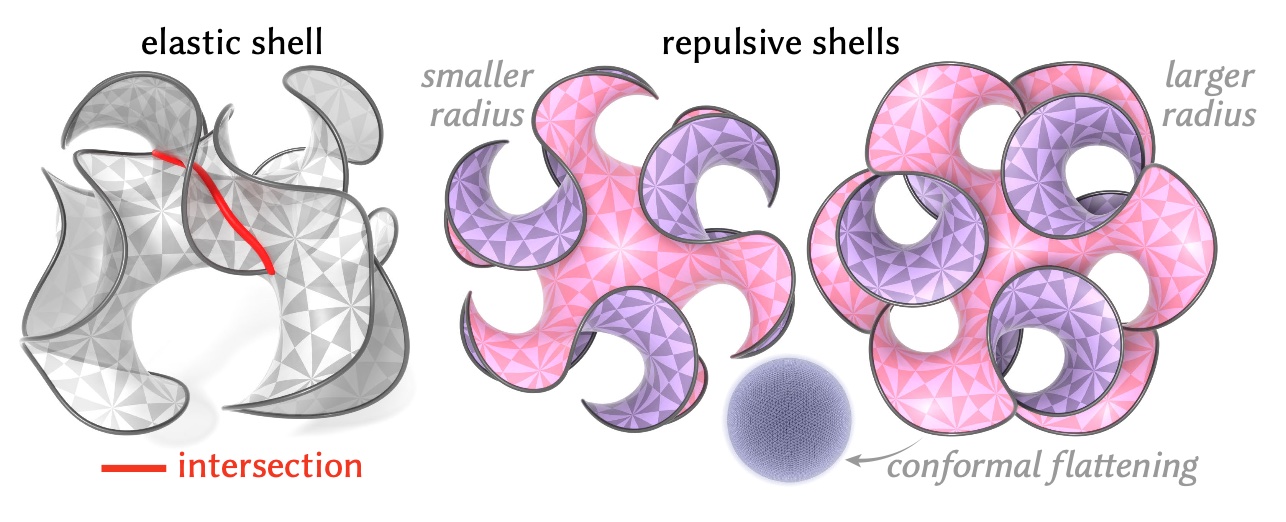
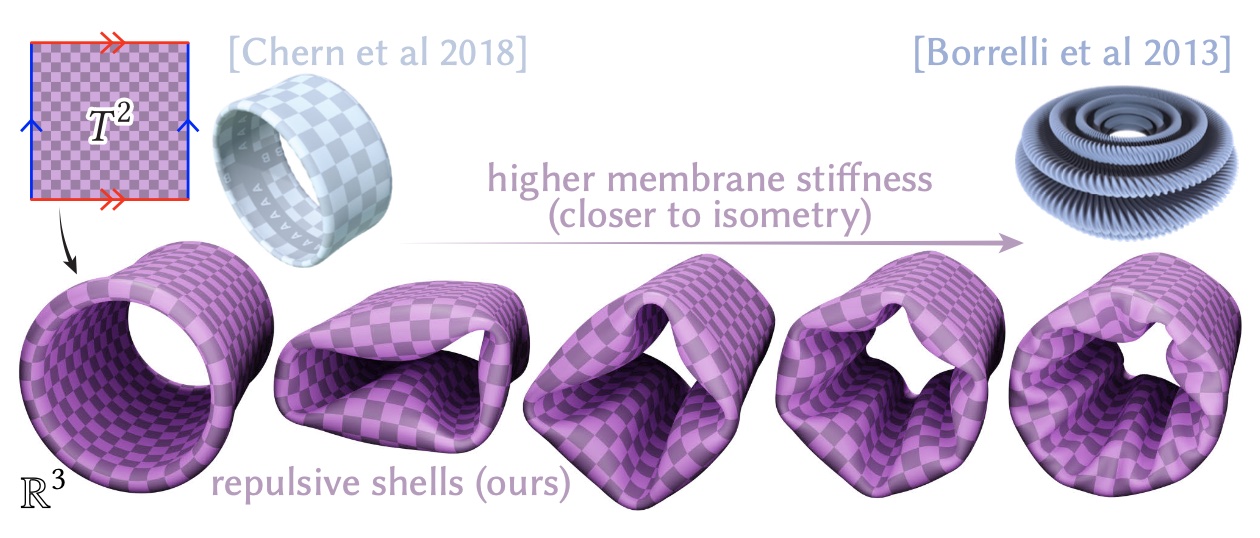
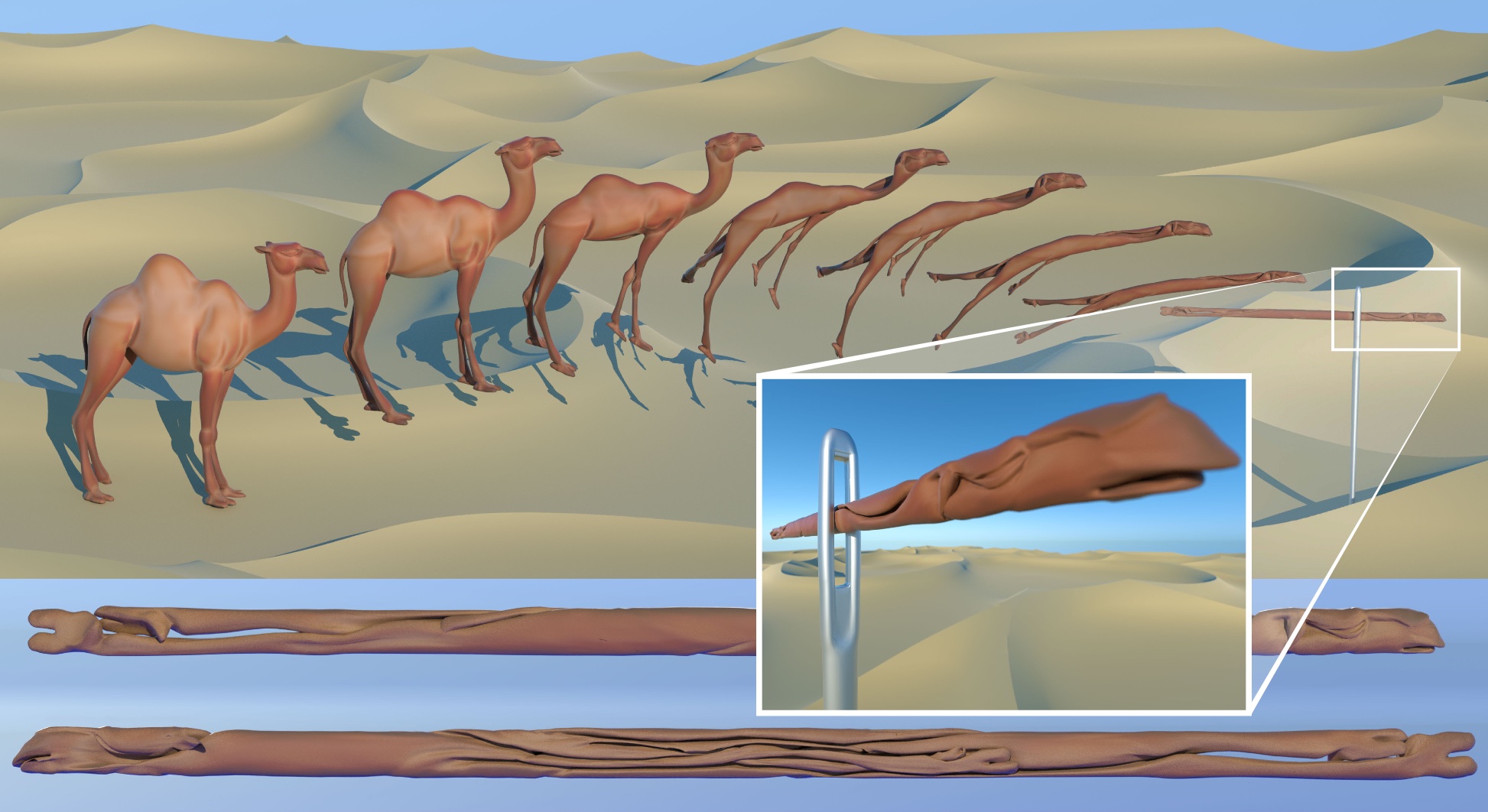
This paper develops a shape space framework for collision-aware geometric modeling, where basic geometric operations automatically avoid interpenetration. Shape spaces are a powerful tool for surface modeling, shape analysis, nonrigid motion planning, and animation, but past formulations permit nonphysical intersections. Our framework augments an existing shape space using a repulsive energy such that collision avoidance becomes a first-class property, encoded in the Riemannian metric itself. In turn, tasks like intersection-free shape interpolation or motion extrapolation amount to simply computing geodesic paths via standard numerical algorithms. To make optimization practical, we develop an adaptive collision penalty that prevents mesh self-intersection, and converges to a meaningful limit energy under refinement. The final algorithms apply to any category of shape, and do not require a dataset of examples, training, rigging, nor any other prior information. For instance, to interpolate between two shapes we need only a single pair of meshes with the same connectivity. We evaluate our method on a variety of challenging examples from modeling and animation.

PDF, 25MB

Video

This work was supported by the Deutsche Forschungsgemeinschaft (German Research Foundation) via project 212212052, project 211504053 – Collaborative Research Center 1060, and Germany’s Excellence Strategy project 390685813 – Hausdorff Center for Mathematics, an NSF CAREER Award (IIS 1943123), NSF Award IIS 2212290, a Packard Fellowship, the German-Israeli Foundation for Scientific Research and Development (grant number I-1339-407.6/2016), and gifts from Facebook Reality Labs, and Google, Inc. Furthermore, this project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 101034255.

Mesh diagrams were created with Penrose.

@article{Sassen:2024:RS, author = {Sassen, Josua and Schumacher, Henrik and Rumpf, Martin and Crane, Keenan}, title = {Repulsive Shells}, journal = {ACM Trans. Graph.}, volume = {43}, number = {4}, year = {2024}, publisher = {ACM}, address = {New York, NY, USA}, }

Figures

Simply penalizing the total repulsive potential over a time-varying trajectory yields undesirable deformation: between the fixed start/end configurations, the surface “explodes” away from itself to reduce potential.

In contrast to forward dynamical simulation, where shapes deform in response to impact, geodesics in our shape space preemptively deform geometry to avoid collisions. Here for instance, a spherical shell “folds up” in anticipation of squeezing through a narrow tube.

Geodesics in the space of repulsive shells correspond to intersection-free trajectories that exhibit natural deformation behavior. Here, for instance, we change the way the fingers of two hands are interleaved by interpolating between two given poses (far left and right), avoiding any intersection even at moments of near-contact. Note also the natural bending of the fingers and wrist to avoid collision, despite the lack of any skeletal rig.

Interpolation between far-left and far-right poses, using a skeletal rig (top), a geodesic in the space of elastic shells (center), and a geodesic in our repulsive shell space (bottom). Notice that the repulsive metric does not merely resolve local intersections near moments of contact—rather, it alters the overall motion plan, yielding different global poses that proactively avoid intersection.

Methods based on injectively deforming the space around an object can struggle with shapes in near-contact due to insufficient spatial resolu- tion. Here we compare shape interpolation via our method (top) versus a method based on divergence-free volumetric flows (bottom).

Timings of energy evaluations. We show the time it takes to evaluate the IPC barrier energy and our adaptive TPE penalty along various trajectories. Notice that in most cases it is faster to evaluate TPE than IPC, even though TPE is an “all pairs” energy. The reason is that we use a fast multipole scheme that reduces evaluation cost from O(n²) to O(n log n).

IPC relies on continuous collision detection (CCD) as a failsafe, since it uses only weak (logarithmic) repulsive forces that do not prevent surface-surface interpenetration in smooth setting. Left: without CCD, using the IPC penalty can yield large self-intersections. Right: our adaptive tangent-point energy still nicely prevents collision, even without expensive collision checks.

When using the IPC barrier as potential energy in our framework, we struggle to find geodesics without sudden “jumps” (more obvious in supplementary video), even with good initialization (top left). Here using the IPC barrier energy for repulsion fails to yield a smooth surface eversion, even after extensive parameter tuning (bottom three rows). A TPE-based formulation easily finds smooth trajectories without jumps (top right).

Progressively packing an octopus (top left) into a small box (bottom right) with a long-range repulsive potential yields a well-separated packing that nicely preserves local geometric features. The result is qualitatively different from a collision-based packing (inset, using reference IDP code), which prevents interpenetration but may not yield a nice global arrangement.

Progressively packing two bunnies into a smaller and smaller sphere (top) yields surfaces that are not only intersection-free, but also nicely distributed throughout the volume (bottom).

We can use our framework to faithfully visualize abstract metrics. Here we isometrically embed a large piece of the hyperbolic plane, obtaining an surface that is both intersection-free and more regular than previous embeddings.

Without the repulsive term, attempts at hyperbolic embedding yield large self-intersections (left). Long-range repulsive forces also help to encourage global symmetry (center, right). A conformal flattening of the final embedded mesh helps verify that the embedding is indeed nearly isometric (bottom right).

Here we compute near-isometric embeddings of a flat metric on the torus. As we increase membrane stiffness (hence get closer to isometry), corrugations naturally arise (bottom)—reminiscent of a Nash–Kuiper embedding (top right), and suggesting better agreement with the target metric than Chern et al. [2018] (top left).

Turning laundry right side out. For each article of clothing we compute a geodesic between a mesh with original and reversed dihedral angles. Intricate, collision-free deformation, like fingertips being inverted as they are pulled through the glove, emerge naturally from the definition of our repulsive metric.

Twisting two cylinders via extrapolation starting from the two leftmost pairs. Without repulsive term, extrapolation would move the cylinders through each other and twist them apart (inset image). However, the repulsive shells exponential map twists the surface into tight configurations.

A leaf naturally rolls up by extrapolating a tiny bend at the tip (top left). Since the initial motion from x⁰ to x¹ slightly increases repulsive energy, the exponential map gradually brings the leaf closer and closer to itself, approaching self-intersection only at time t = ∞. Meanwhile, the elastic part of the metric preserves surface detail and guides the overall motion.

Inversion of cut-open sphere. Top: Discrete geodesic interpolation without repulsion (green to purple). Bottom: Geodesic interpolation with repulsion (blue to red). The fixed surface boundary is shown as yellow curve.

The optimal trajectory of a surface depends on the interaction between elastic and repulsive forces—here we show variations of Figure 4 with stronger (top) and weaker (bottom) bending stiffness. The full obstacle geometry is shown in the inset.

Passing a camel through the eye of a needle. The initial mesh (far left) is first progressively compressed into a cylinder (far right); we then find a geodesic between initial and compressed states (left to right). Bottom: close-up of compressed geometry from left/right sides; inset shows occluded piece.