Repulsive Surfaces
ACM Transactions on Graphics 2021

Functionals that penalize bending or stretching of a surface play a key role in geometric and scientific computing, but to date have ignored a very basic requirement: in many situations, surfaces must not pass through themselves or each other. This paper develops a numerical framework for optimization of surface geometry while avoiding (self-)collision. The starting point is the tangent-point energy, which effectively pushes apart pairs of points that are close in space but distant along the surface. We develop a discretization of this energy for triangle meshes, and introduce a novel acceleration scheme based on a fractional Sobolev inner product. In contrast to similar schemes developed for curves, we avoid the complexity of building a multiresolution mesh hierarchy by decomposing our preconditioner into two ordinary Poisson equations, plus forward application of a fractional differential operator. We further accelerate this scheme via hierarchical approximation, and describe how to incorporate a variety of constraints (on area, volume, etc.). Finally, we explore how this machinery might be applied to problems in mathematical visualization, geometric modeling, and geometry processing.
Video
Talk Video
repulsive-surfaces—implementation in C++
The authors thank Saul Schleimer and Henry Segerman for helpful discussions about topological examples, and Nick Stadie for perspective on molecular symmetries. This work was supported by a Packard Fellowship, NSF Award 1943123, and gifts from Autodesk, Activision Blizzard, Adobe, Disney, and Facebook. The third author was supported by DFG-Project 282535003: Geometric curvature functionals: energy landscape and discrete methods.
@article{Yu:2021:RS,
author = {Yu, Chris and Brakensiek, Caleb and Schumacher, Henrik and Crane, Keenan},
title = {Repulsive Surfaces},
journal = {ACM Trans. Graph.},
volume = {40},
number = {6},
year = {2021},
publisher = {ACM},
address = {New York, NY, USA},
}
Figures
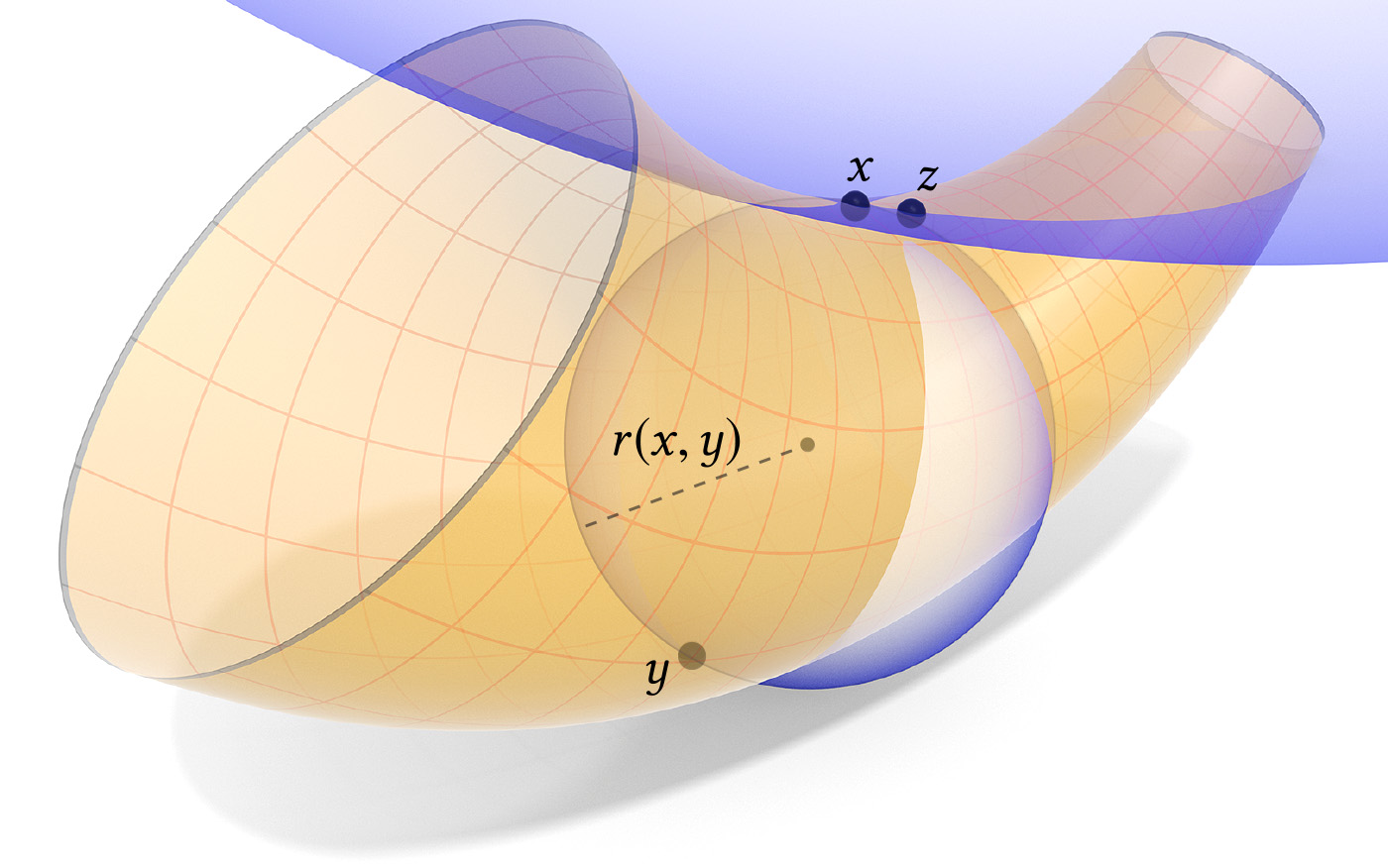
For each pair of points x,y on the surface, the tangent-point energy considers the radius r(x,y) of the smallest sphere tangent to x and passing through y, penalizing 1/r(x,y). Hence, the contribution will be very large for points y close in space but distant along the surface—and small for points z nearby along the surface, where the radius is huge.
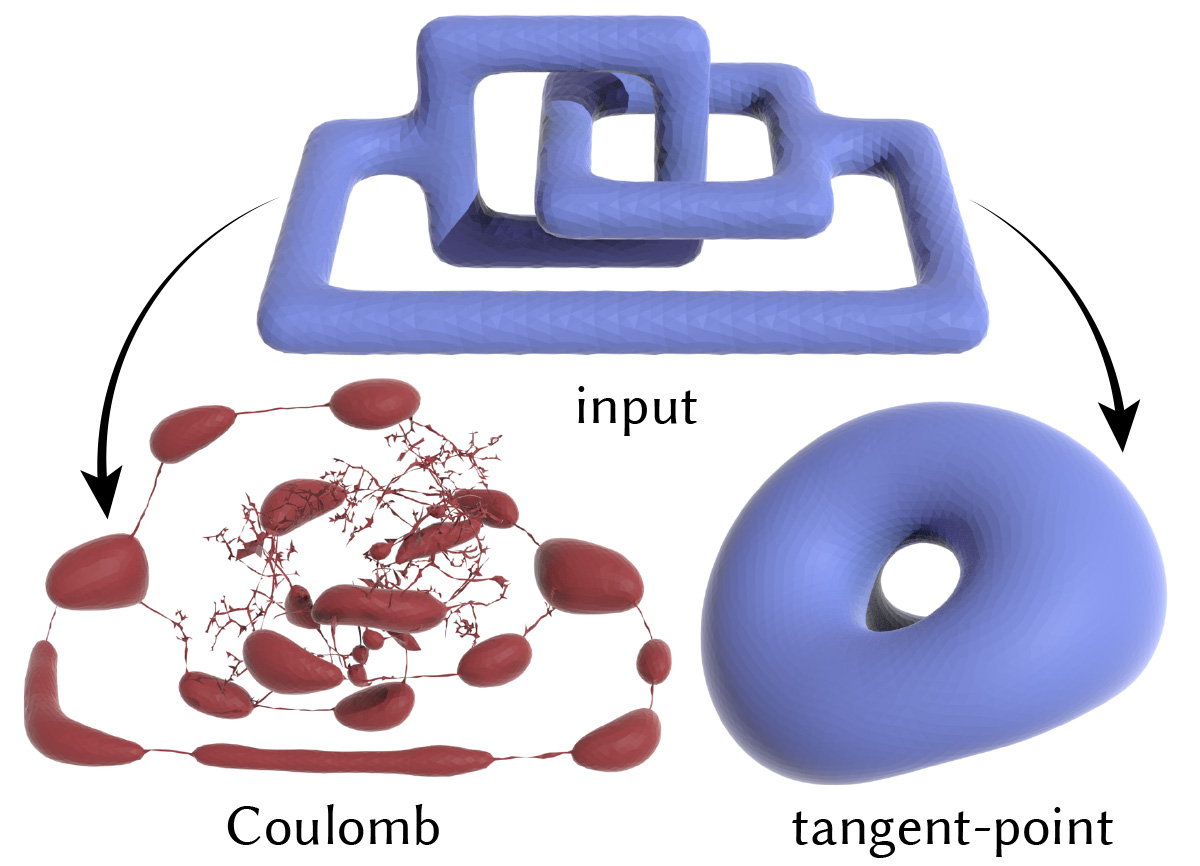
Ad-hoc schemes such as vertex-vertex Coulomb forces do not correspond to a meaningful smooth energy and can be numerically unstable. Here we minimize Coulomb and tangent-point energies subject to a fixed area constraint.
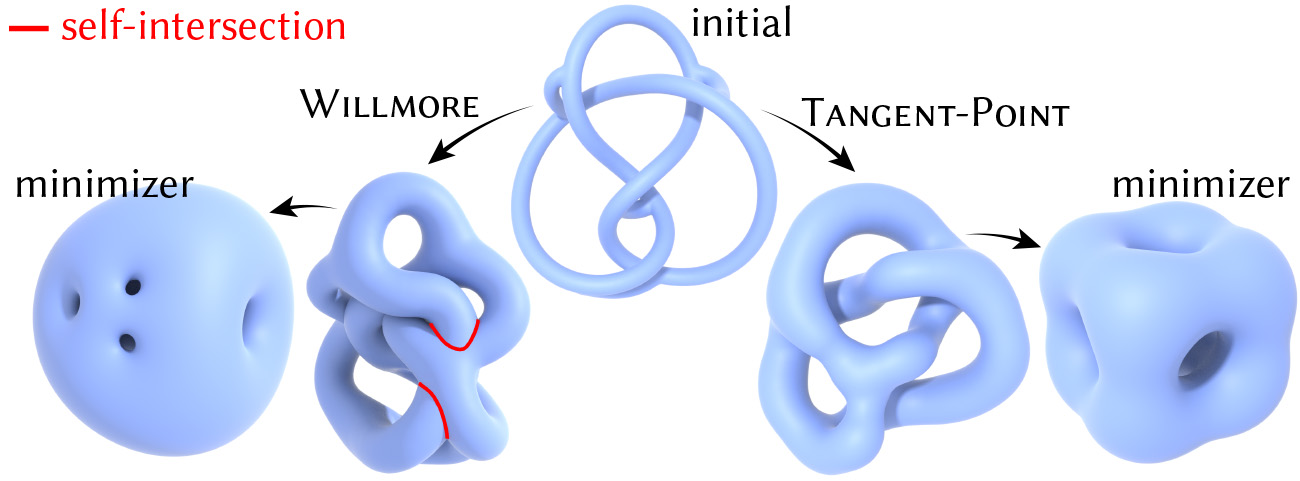
Willmore energy does nothing to prevent intersections (in red), and can have minimizers that asymmetrically distribute curvature over the surface. Right: tangent-point energy avoids intersections and tends to provide a more uniform curvature distribution.

Unlike other numerical schemes, our fractional preconditioner does not suffer from a mesh-dependent time step restriction. Here for example we take 300 optimization steps of maximum size (determined by line search) for each scheme. As resolution increases, all methods but Hs make slower and slower progress. Note also that schemes based on H1 preconditioning (H1, H1 L-BFGS, AQP, BCQN) quickly eliminate high-frequency details but are slower to smooth the bulk shape; conversely, H2 quickly smooths out the bulk shape but fine details remain. Using Hs for 1 < s < 2 nicely handles both local and global features.

Gallery of isotopies obtained by minimizing tangent-point energy—notice that highly knotted surfaces, as well as surfaces with thin sheets and handles, successfully flow to their canonical embeddings. Surfaces are grouped by their isotopy equivalence classes, which are extremely difficult to determine via visual inspection (and also not simply determined by Euler characteristic—see table of knotted embeddings below).

Top: even careful illustrations of topological phenomena (here drawn by mathematician Peter Lynch) can be difficult to understand without a good visual imagination. Bottom: our method automatically generates continuous motions that are easier to interpret (see video), enabling exploration by students and researchers who do not have significant artistic training.
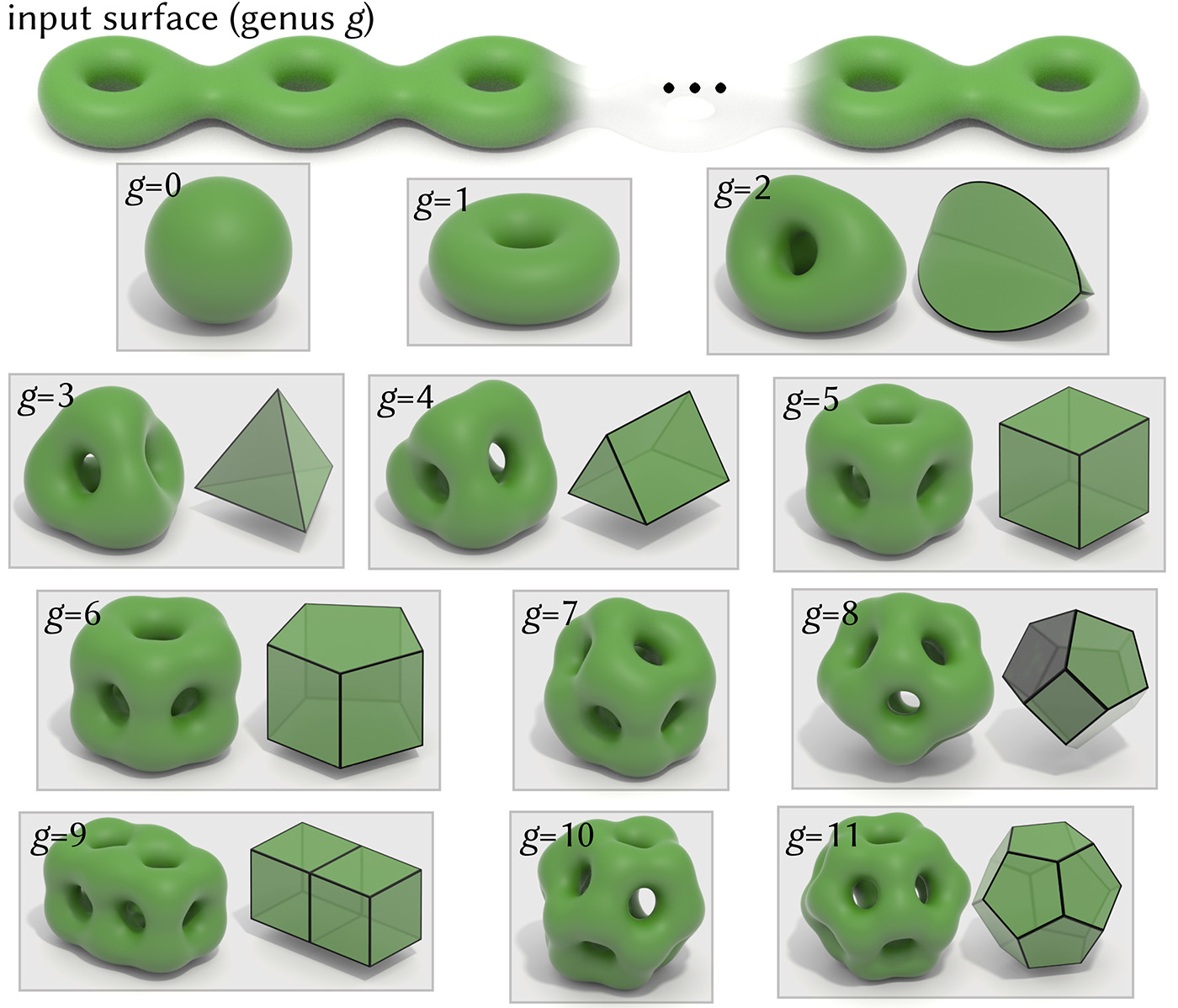
Global minimizers of geometric energies provide canonical domains that can be used to map between surfaces of the same topology, or simply help visualize a topological space. Here we show conjectured minimizers of the tangent-point energy for unknotted surfaces of genus g; adjacent figures illustrate symmetries (when present).

Geometric functionals provide a bridge between topology and geometry by enabling one to construct canonical geometric representatives of a given topological space. Here, minimizers of tangent point energy are used to visualize nontrivial isotopy classes of a genus-2 surface. (Numbers indicate number of crossings; subscripts index trivalent graphs from Ishii et al 2012, Table 1).
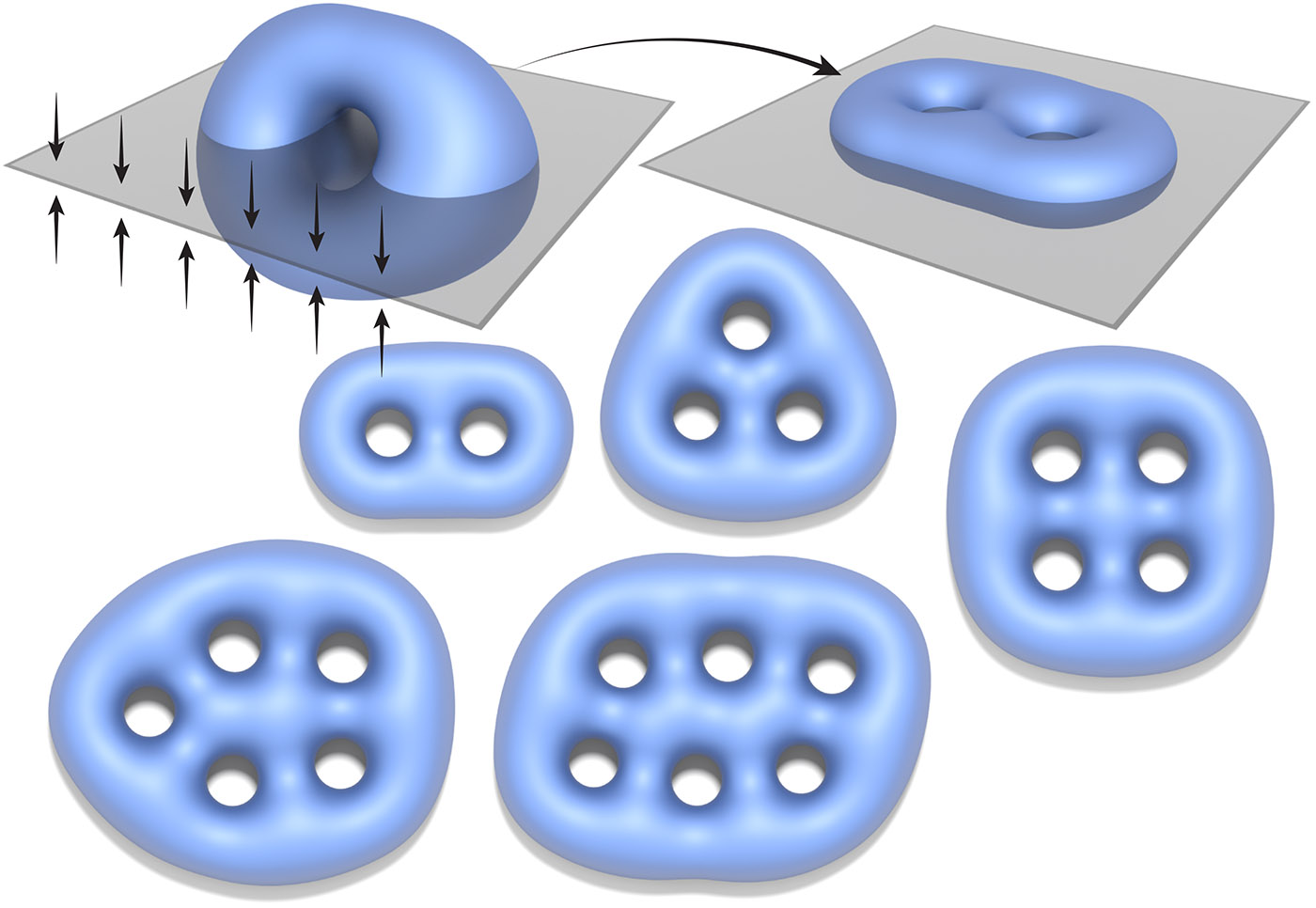
Top: minimizers of tangent-point energy often exhibit three-dimensional symmetries which can be difficult to understand from a single view—by adding an attracting plane, we get embeddings that can be nicely displayed in two-dimensional illustrations. Bottom: constrained minimizers for genus 2 through 6.

Surprisingly, one can remove a handle of a double torus from a loop or pole without cutting or pinching the surface. Top: hand-drawn illustration by David Wells. Bottom: isotopy computed automatically by our method (see video); no keyframing or boundary conditions were used.
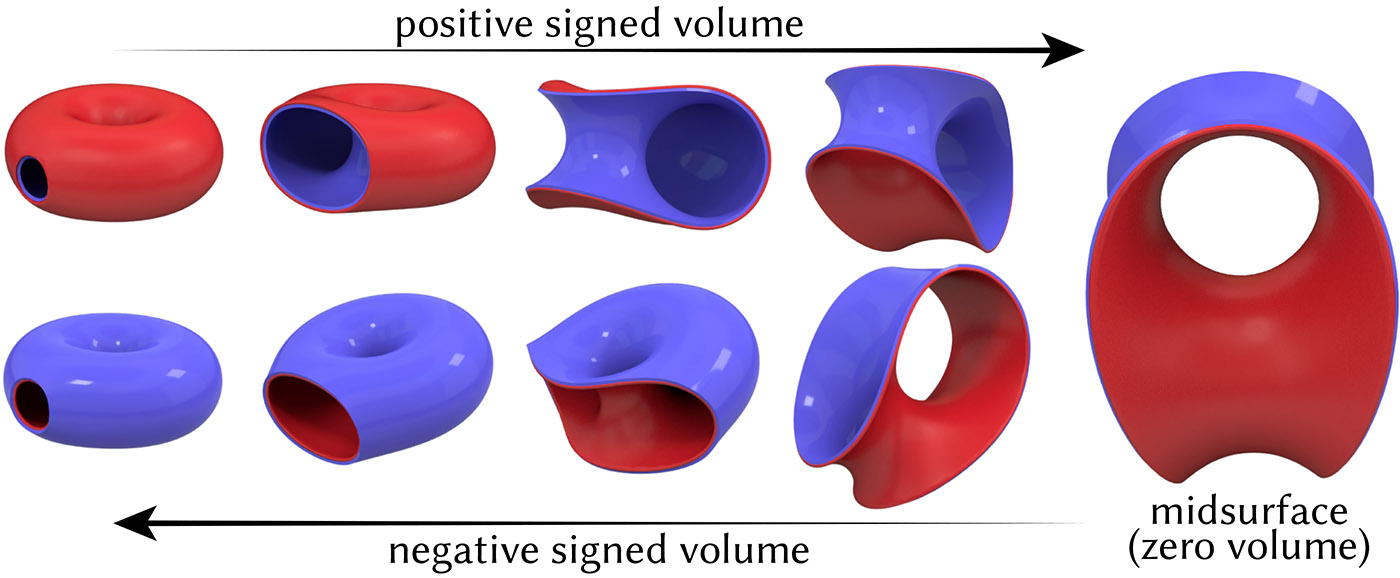
Minimizing the tangent-point energy of a punctured torus while pushing signed volume toward zero yields a surface with reflection symmetry. Applying a reflection and reversing the flow hence yields an eversion that turns the surface ``inside-out'' while avoiding self-intersections.

The tangent-point energy can be used to make variational surface modeling responsive to proximity, rather than just collisions. Here for instance we pin a sparse or dense set of points and modify volume and surface area to adjust the appearance of some text (in some cases enclosed in a box). Like Willmore energy (top right), we get smooth behavior near point constraints (see magnified portion), but avoid overlap.
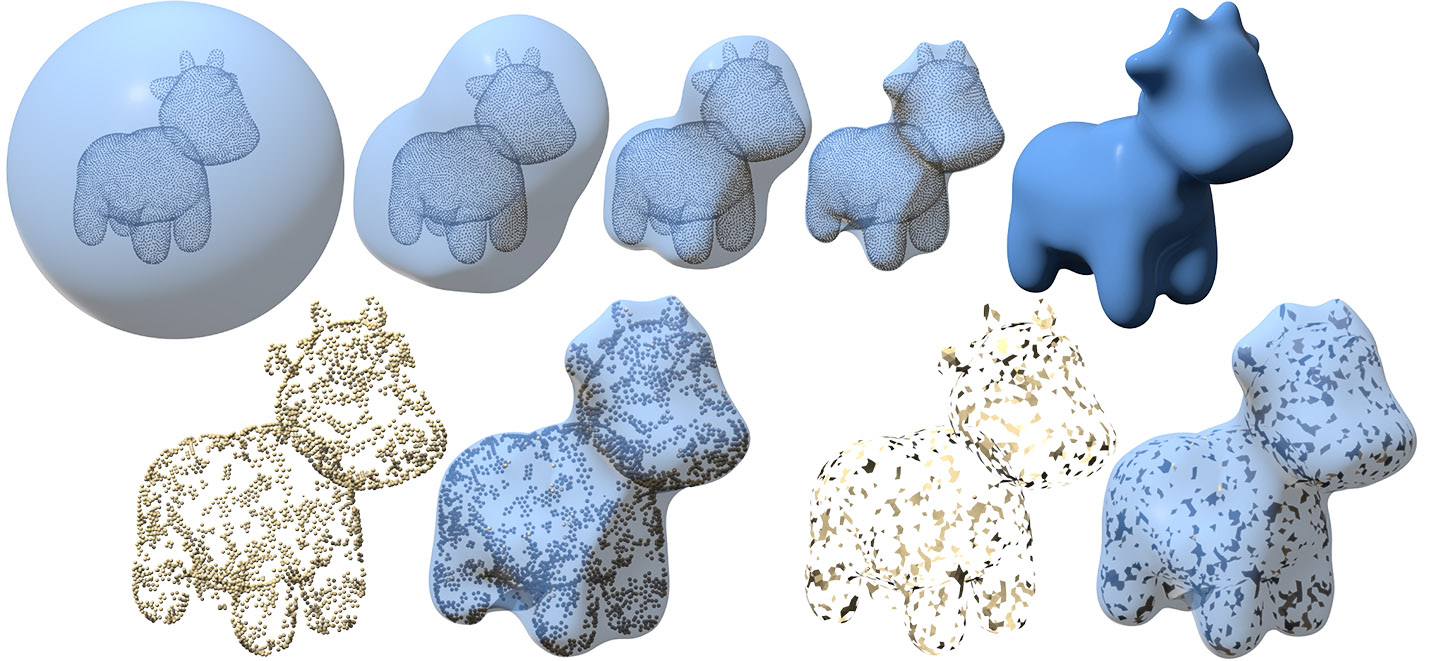
Here we perform a simple ``shrink wrapping'' to obtain a manifold, intersection-free reconstruction (top), which works well even for points or polygon soup with severe holes and missing data.

We can also ``shrink wrap'' a model to get a sequence of progressively coarser approximating envelopes that exhibit a strict containment property, and are free of self-intersection. Here we aim for a 1.15x increase in volume at each level.

We can also use tangent-point energy for generative modeling by ``growing'' a surface subject to constraints. Top: confining to a sphere while increasing area leads to a wrinkled shape reminiscent of a walnut. Bottom: growing many small spheres inside a slab yields a tileable cobblestone pattern.

Fast positional constraints enable Dirichlet boundary conditions. Here, minimizing tangent-point energy on a cylinder yields a nearly spherical geometry (left). Using tangent-point energy to regularize area minimization avoids the usual pinch-off singularities in minimal surfaces (center). We can also compute (near-)minimal surfaces with obstacles, in the spirit of [Giusti 1973] (right).
