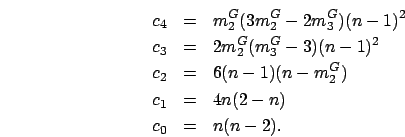- ... time1.1
-
The response time of a job refers to
the time from when the job arrives until it is
completed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variables)1.2
-
We consider only continuous time systems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
system1.3
- An M/M/
 /FCFS system has a single queue and
/FCFS system has a single queue and  servers, where jobs arrive according to a Poisson process, and the
service demand has an exponential distribution. The jobs are served
in the order of their arrivals (first-come-first-served, FCFS).
servers, where jobs arrive according to a Poisson process, and the
service demand has an exponential distribution. The jobs are served
in the order of their arrivals (first-come-first-served, FCFS).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
systems1.4
- These systems refer to a single server system and a
multiserver system with the same service capacity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
policies1.5
- These common task assignment policies include the
round robin policy, the shortest queue policy, and the least remaining
work policy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... subset2.1
-
Likewise, the Complete and Positive solutions are not
numerically stable for a small subset of input distributions, but
this is not a problem in practice, since distributions lying in
the small subset can be perturbed to move out of the subset. (In
[146,145], we also provide a version of the Complete
solution that is numerically stable for all input distributions.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... chain2.2
-
Throughout, a Markov chain is assumed to be a continuous time Markov chain.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
background process3.1
-
We also assume that there exists a level
 in the background process such that the behavior of the
foreground process stays the same while the background process is in
levels
in the background process such that the behavior of the
foreground process stays the same while the background process is in
levels  . For example, in an M/M/2 queue with two priority
classes, the behavior of the low priority jobs (foreground process)
stays the same while there are
. For example, in an M/M/2 queue with two priority
classes, the behavior of the low priority jobs (foreground process)
stays the same while there are  high priority jobs (background
process is in levels
high priority jobs (background
process is in levels  ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 3.2
3.2
-
In the literature, the standard notation is ``
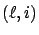 ,''
where the level is followed by the phase. In this thesis, we choose
,''
where the level is followed by the phase. In this thesis, we choose
 , because a level (respectively, phase) corresponds to a column (respectively, row)
in our figures of Markov chains. Notice that (row,column) is a standard matrix notation.
, because a level (respectively, phase) corresponds to a column (respectively, row)
in our figures of Markov chains. Notice that (row,column) is a standard matrix notation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
equation3.3
-
Any other nonnegative solution
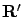 of (3.5)
satisfies
of (3.5)
satisfies
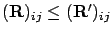 for all
for all  and
and
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model3.4
- The coupled processor model is
related to cycle stealing without switching cost
(Figure 3.1(a)). In this model two processors each serve
their own class of jobs, and if either is idle it may help the other,
increasing the rate of the other processor. This help incurs no
switching time and has a benefit even if only a single job is present
(i.e. two processors can work on the single job).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
process3.5
-
In [151,152], we analyze this system by reducing the
2D Markov chain into a 1D Markov chain but without modeling it as a
GFB process. The approach in [151,152] requires
identifying and analyzing multiple types of busy periods for this
particular system.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
process3.6
-
In [67], we analyze the SBCS-CQ with an additional
technique to reduce mean response time, renaming of servers (see Chapter 5).
With renaming, the SBCS-CQ does not appear to be modeled as a GFB
process, and in [67] we introduce an approximation in
the analysis via DR.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zero3.7
- A motivation for using threshold-based policy under zero switching times may be to
reduce some ``cost,'' such as money and risk, involved in the
switching.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... satisfied3.8
-
The first condition is based on the assumption that the sample mean has a normal distribution when
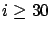 ,
and the second condition is based on the Chebyshev's inequality on the sample mean. In both cases,
the true variance is assumed to equal to the sample variance.
,
and the second condition is based on the Chebyshev's inequality on the sample mean. In both cases,
the true variance is assumed to equal to the sample variance.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution3.9
-
To determine
the parameters of the two phase Coxian
 PH distribution, the third
moment needs to be specified as well. Here, we choose the third
moment, so that the normalized second and third moments,
PH distribution, the third
moment needs to be specified as well. Here, we choose the third
moment, so that the normalized second and third moments, 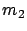 and
and
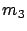 , satisfy
, satisfy  . See Section 2.5 for an
intuition for this choice; in particular, the exponential
distribution and the Erlang distribution satisfy
. See Section 2.5 for an
intuition for this choice; in particular, the exponential
distribution and the Erlang distribution satisfy  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... evaluated3.10
- Although DR-CI can be evaluated with
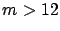 (see Figure 3.36), it is hard to have simulation
converge with
(see Figure 3.36), it is hard to have simulation
converge with 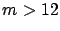 . Note that the fraction of arrivals of jobs with
the largest size is very small: on average, there is only one arrival
of a job with the largest size while there are
. Note that the fraction of arrivals of jobs with
the largest size is very small: on average, there is only one arrival
of a job with the largest size while there are  arrivals of
jobs with the smallest size. When
arrivals of
jobs with the smallest size. When  , more than 1,000,000,000
events are needed for simulation to converge.
, more than 1,000,000,000
events are needed for simulation to converge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... level3.11
- Observe that
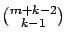 is the number of
states with at most
is the number of
states with at most  higher priority jobs (i.e., the number of
ways to assign at most
higher priority jobs (i.e., the number of
ways to assign at most  higher priority jobs to
higher priority jobs to  homogeneous
servers), and
homogeneous
servers), and
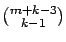 is the number of states with
is the number of states with  higher priority jobs.
higher priority jobs.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)4.1
-
To determine
the parameters of the two phase PH distribution, the third
moment needs to be specified as well. Here, we choose the third
moment, so that the normalized second and third moments,
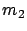 and
and
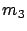 , satisfy
, satisfy  . See Section 2.5 for an
intuition for this choice; in particular, the exponential
distribution and the Erlang distribution satisfy
. See Section 2.5 for an
intuition for this choice; in particular, the exponential
distribution and the Erlang distribution satisfy  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)4.2
-
To determine the parameters of the two phase PH distribution, the
third moment needs to be specified as well. Here, we choose the third
moment, so that the normalized second and third moments,
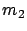 and
and
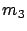 , satisfy
, satisfy  . See Section 2.5 for an
intuition for this choice; in particular, the exponential distribution
and the Erlang distribution satisfy
. See Section 2.5 for an
intuition for this choice; in particular, the exponential distribution
and the Erlang distribution satisfy  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:compare)4.3
-
The third moment of the two-phase PH distribution is chosen as before.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution5.1
-
To determine
the parameters of the two phase PH distribution, the third
moment needs to be specified as well. Here, we choose the third
moment, so that the normalized second and third moments,
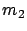 and
and
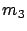 , satisfy
, satisfy  . See Section 2.5 for an
intuition for this choice; in particular, the exponential
distribution and the Erlang distribution satisfy
. See Section 2.5 for an
intuition for this choice; in particular, the exponential
distribution and the Erlang distribution satisfy  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stealing6.1
-
Other systems that support process migration include
Charlotte [11], Accent [211],
Mach [128], Emerald [91],
Tue [179], and Locus [191].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time7.1
-
That is, when
![$\sum_{i=1}^2c_ip_i^L\mbox{{\bf\sf E}}\left[ R_i^L \right] \sim
\sum_{i=1}^2c_ip_i^H\mbox{{\bf\sf E}}\left[ R_i^H \right]$](img1715.png) , where
, where 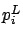 (respectively,
(respectively, 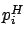 )
is the fraction of jobs that are type
)
is the fraction of jobs that are type  and arriving during the low (respectively, high) load period,
and
and arriving during the low (respectively, high) load period,
and
![$\mbox{{\bf\sf E}}\left[ R_i^L \right]$](img1718.png) (respectively,
(respectively,
![$\mbox{{\bf\sf E}}\left[ R_i^H \right]$](img1719.png) ) is the mean response time of type
) is the mean response time of type  jobs arriving
during the low (respectively, high) load period, for
jobs arriving
during the low (respectively, high) load period, for  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zeroB.1
-
In [22], Bobbio et al. also provide a closed form solution for mapping
any
 to a minimal-phase general acyclic PH distribution,
which can have mass probability at zero
(i.e. the number of phases used is
to a minimal-phase general acyclic PH distribution,
which can have mass probability at zero
(i.e. the number of phases used is  ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stepsB.2
-
 is a solution for the fourth order equation
is a solution for the fourth order equation
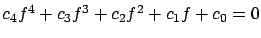 , where
, where
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.