1-d Arrays, The Object class, and Simple Collections

Advanced Programming/Practicum
15-200

Introduction In this lecture, we will discuss a powerful aggregate data structure: arrays. Arrays allow us to store collections of arbitrary-sized sequences of values (both primitive types and references to objects), and easily access and manipulate all these values. We will learn how to declare arrays, picture them, and perform operations on arrays (mostly by looping, and performing operations on the individual values in the arrays). We will examine how arrays can be used as instance variables in classes.

Once we have learned the basic array material, we will discuss wrapper classes and the Object class. Putting all this information together, we will learn how to represent two simple, general, and powerful collection classes (stack and queue) with expandable arrays stored as instance variables. We will follow-up on this material later in the semester, with a systematic study of even more powerful Java collection classes.

Arrays are very similar to objects from a special class, and we will exploit this similarity throughout our discussion of arrays. There is also a strong connection between arrays (which are indexed by a sequence of integers) and for loops (which easily generate a sequence of such integers). Finally, there is also a connection between files and arrays: often the information stored in a file (easily processed sequentially) is read and stored into an array (where it can be easily and efficiently processed -and reprocessed- either sequentially or randomly).

Declaring
(and initializing)
Arrays		 We declare and initialize array variables like other class variables, but by specifying the type and constructor in a special form: for 1-dimensional (1-d) arrays, the type is specified as any Java type (primitive or reference) followed by []; the constructor uses that same type, with an int value (computed by a literal or more general expression) inside the brackets. The value computed from this expression specifies the length of the array: how many values it contains. Once we construct an array object, its length may not change: there is no mutator for that operation. So, for example, we can declare and initialize an array variable storing a reference to an object containing 5 ints by the declaration 
  int[] a = new int[5];
This variable, and the object it refers to, are illustrated in the following picture.

  Pronounce [] as "array"; so int[] is pronounces as "int array". Array objects are labelled by their array type; they contain two major parts: a sequence of indexed boxes and a special box named length. Notice four important facts about arrays illustrated by this picture.
  • An array is a homogeneous data structure: each of its indexed members is labelled by (and stores) the same type (here int). Constrast this with the other classes that we have discussed, which are heterogeneous: each of their instance variables can store a different type. We can declare arrays to store sequences of either primitive or reference types. Because this is an int[], each box in the sequence stores an int value, and is so labelled. Each box in the sequence is also labelled by its index (0, 1, 2, etc.) which is always an int no matter what type is stored inside each box.

  • The indexes are numbered from 0 to one less than the length of the array (here the maximum index is 4, which is one less than the length of the array, which is 5). This decision, while elegant from a mathematical perspective, is a disaster from a psychological perspective: most humans start counting at 1, not 0, and most of us expect the length of the array to be the same as the index of the last box in the array. But C, C++, and Java all start the indexes of their arrays at 0, so, we must overcome human nature when we use arrays in programming.

  • Each array object defines a public final int length instance variable that stores the length of the array. Its value is specified when the array object is constructed, and is unchangeable after that: because length has the final access modifier, we CANNOT attempt to change its value. But, we can directly access (i.e., not through an accessor) the value stored in this field. In this example, we could write a.length in our code: it is an expression that evaluates to 5. In fact, we can always specify the highest legal index in the array object by the expression a.length-1. So given a reference to an array, we can always determine its length, and from it the highest index.

  • Like all instance variables, ALL INDEXED MEMBERS ARE AUTOMATICALLY INITIALIZED when the array object is constructed. Java initializes them as it initializes all instance variables: for the primitive types, it uses 0 for int, 0. for double, false for boolean, and the null character for char; for all reference types it uses null (meaning that they do not refer to any object). Here all the indexed members are initialized to 0.

We must use only non-negative lengths when we construct arrays objects (a length of 0 is allowed, and does have some interesting uses). If we specify a negative value, the special constructor for arrays throws the NegativeArraysSizeException.

We can also construct an array by declaring all the values that it must contain; in such a case, the length of the array is automatically inferred from the number of values. So, for example, we can declare and initialize an array variable storing a reference to an object containing the five int values 4, 2, 0, 1, and 3 (in that order) by the declaration 

  int[] a = new int[]{4, 2, 0, 1, 3};
If you think about int[] as the class name and {4,2,0,1,3} as the parameters to the constructor for an object from that class, this syntax is reasonable. Of course, we cannot take this similarity too far, because constructors always have a set number of parameters, while any number of arguments are allowed between these braces. The types of all the values in the braces must be compatible with the type of the array used in the constructor.

We illustrate the result of executing this declaration by the following picture.

 
Accessing Arrays by their Indexed Members We can access any individual member stored in an array object by using
  • the variable that refers to the array object,
  • and the index of the member that we want to access (written as an expression inside brackets).
So, if we declare int[] a = new int[]{4, 2, 0, 1, 3}; then we can write System.out.println( a[0] ); Java would print the value stored in index 0 in array a, which is 4. We pronounce a[0] as "a at index 0" or just "a sub 0" (similar to the subscript in mathematical notation: think of the sequence a0, a1, a2, etc.) Likewise, we can write 
  if (a[2] == 0)
    ...some statement
which checks to see whether or not zero was stored in the array object referred to by a, at index 2.

Note that a is of type int[] (pronounced int array); any access to a member stored in an index of a is of type int. Generally, if a is of type T[] (pronounced t array), then any access to a member stored in an index of a is of type T.

The golden rule of arrays says, "Do unto any array member as you would do unto a variable of the same type". So wherever we can use an int variable, we can use an int[] member. Thus, we can write a[2] = 8;, using a[2] on the left side of the = state-change operator (changing the value stored in index 2 from 0 to 8). We can even write a[2]++;, which increments the value stored in index 2 of the array. So, when you ask yourself the question, "Can I use access an array member and use it here?", the question simplifies to, "Can I use a variable (of the same type) here?"

In fact, the value written inside the brackets can be any expression that evaluates to an int; we will see how variables and more complicated expressions are used for indexing arrays later in this lecture. For now, note that writing a[a.length-1] = 0; stores 0 in the last index of the array object.

Note that when accessing a member in an array, if the value computed for the index is less than 0, or greater than OR EQUAL TO the length of the array, then trying to access the member at that index causes Java to throw the ArrayIndexOutOfBoundsException which contains a message showing what index was attempted to be accessed. So, writing a[a.length] = 0; throws this exception, since the index 5 is not in the array object.

Finally, here is a picture that shows how to declare a variable refering to an array object, but this time the array object stores a String in each index. After this declaration are three expression statements that intialize these indexes with new String objects.

  Although indexes are always integers, the values stored at each index depends on the type used to declare/construct the array. In this example, each index stores a reference to a String object. Finally, using what we learned above, we could have declared and intialized this variable and its array object in just one declaration: by either 
String[] s = new String[]{new String("ABC"), new String("LMN"), new String("XYZ")};
String[] s = new String[]{"ABC", "LMN", "XYZ"};
  The second, more simple, declaration is correct because of the special property of String literals that they construct their own objects.

Note that because of the golden rule, we can use s[0] just like any variable of type String; therefore, we can write the expression s[0].length() which returns 3 (the length of the String object referred to in index 0 in the String array s). So generally, when arrays store references to objects in their indexed members, we can call an appropriate method (based on the type of the reference) on any member in the array. Here we can call any String method on any object stored in this array.

Processing Arrays Most code that processes an array does so by iterating through it: looking at the value stored in each indexed member in the array object. Typically, a for loop is used to generate all the indexes for the array object. Study the following code carefully; although short, it contains all the fundamentals that you need to understand for writing array processing code. This code computes the sum of all the values in an int[]. 
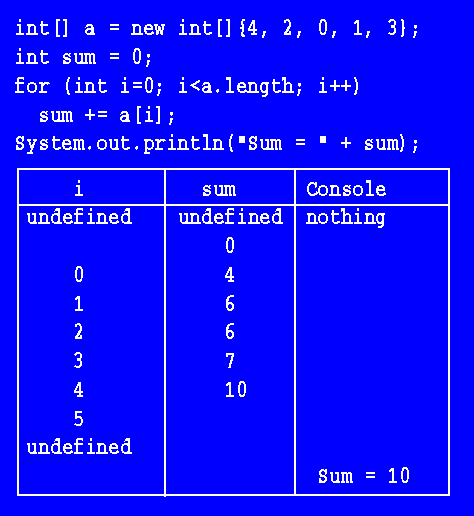
  int sum = 0;
  for (int i=0; i<a.length; i++)
    sum += a[i];
  System.out.println("Sum = " + sum);
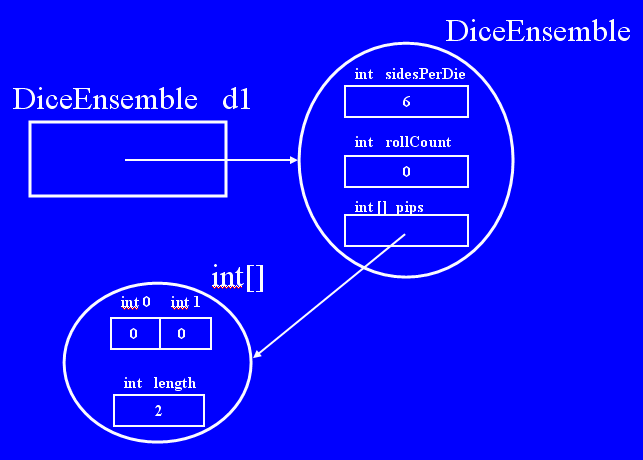
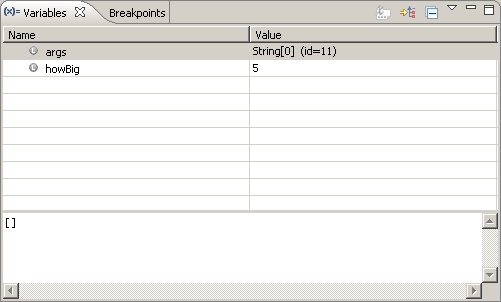
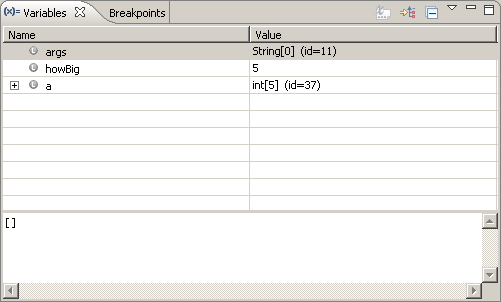
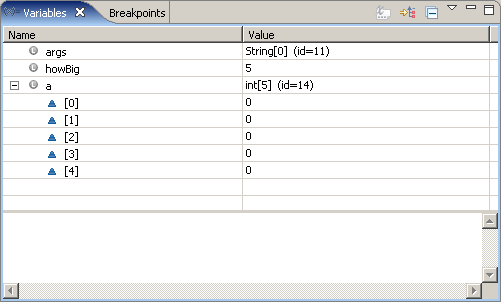
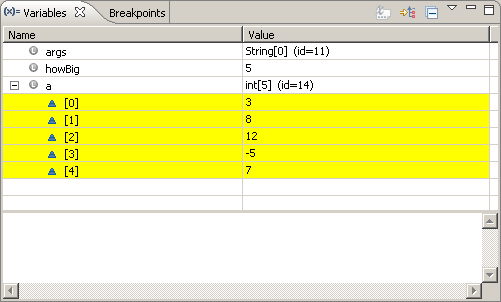
Below is a (non-compact) trace table that illustrates the hand simlation of this code. Notice how the same statement sum += a[i]; is repeatedly executed, but it has a slightly different meaning every time, because the value stored in i changes, so the indexed member being added to sum is always different.

Notice the for's continuation test: i<a.length. When the length is 5 (as in this example), the final i for which the body is executed is 4(the highest index in the array); when i increments to 5, the test is false for the first time, so the body is not executed, and instead the loop is terminated. We can write this test as i<=a.length-1, which has the same meaning, but few "real" programmers write the test this way.

The following code prints on one line, separated by spaces, all the values stored in an array. After all the values are printed (and the loop terminates), it ends the line. Notice that the same for loop code is used (this time to examine and print, not add together) every member stored in the array object; only the body of the loop (telling Java what to do with each indexed member) is different. 

  for (int i=0; i<a.length; i++)
    System.out.print(a[i]+" ");
  System.out.println();

Below, a more interesting version of this loop prints a comma-separated list of values stored in the array: the last one is not followed by a comma, but by a new line. The String to catenate is decided by a conditional expression. 

  for (int i=0; i<a.length; i++)
    System.out.print( a[i]+(i<a.length-1?",":"\n") );

The following code prompts the user to fill in each value in an array. Notice that the same for loop code is used (this time to store into every indexed member in the array object); again, only the body of the loop is different. 

  for (int i=0; i<a.length; i++)
    a[i] = Prompt.forInt("Enter value for a["+i+"]");

The following code computes and prints the maximum value stored in an array. Because the original maximum value comes from index 0 in the array (the first value stored in the array), the for loop starts at index 1 (the second value stored in the array). 

  int max = a[0];
  for (int i=1; i<a.length; i++)
    if (a[i]>max)
      max = a[i];
  System.out.println("Max = " + max);
We also could have also written this code as follows, initializing max to Integer.MIN_VALUE and starting the for loop at index 0, guaranteeing a[0]'s value will be stored into max during the first loop iteration. 
  int max = Integer.MIN_VALUE;
  for (int i=1; i<a.length; i++)
    if (a[i]>max)
      max = a[i];
  System.out.println("Max = " + max);

Examine the Javadoc for the Integer class to learn about this public static final int value. Then, hand simulate this second loop to understand why/how it works. In fact, we could replace the if statement by either max = Math.max(max,a[i]); or max = (a[i]>max ? a[i] : max); and compute the same result, although I prefer the if statement.

Finally, the following code loads all the information from a file into an array. We often perform this operation early in a proagram, and then process the information in the array one or more times, beause it is easier to manipulate the information in an array than a file. To work, the file must first store the length of the array needed; it is read first and used to construct an array object exactly the right size to store all the remaining values. Then, we must read the remaining values from the file individually, and store them into the array. 

  TypedBufferReader tbr = 
    new TypedBufferReader("Enter file to load in array");
  String[] s = new int[tbr.readInt()];
  for (int i=0; i<a.length; i++)
    a[i] = tbr.readString();
  tbr.close();
Note that we have omitted a try/catch block for catching exceptions: we are assuming that the file contains all correct data, and we never try to read past the last data value in the file. Of course, writing this code in a block allows us to decide how to handle exceptions (wrong type of data, not enough data, etc).

The Array Demonstration application contains all the code described in this section (and more). Please download, unzip, run, and examine this code (it is discussed again in the secion illustrating how arrays appear in the Eclipse debugger).

Strings As Arrays A brief observation. The String reference type also has "array-like" properties: a String is a sequence of characters and you can access the individual chars in a String. There are a few relevant differences to know (also check out this material in Sun's Javadoc for the String class). Assume that we declare String s = "ABC";
  • Unlike arrays, Strings employ a public int length method (not a public instance variable) for accessing the length of the String. Thus we must write something like s.length() (which returns 3); this inconsistency is foolish.
  • Unlike arrays, Strings employ a charAt method (not []) for accessing the char at a specified index in the String (e.g., s.charAt(0), which is 'A'. Because this class is immutable, there is no way to change the character stored at an index.
  • Unlike arrays, when accessing an illegal index in a String (with charAt), Java throws StringIndexOutOfBoundsException (not ArrayIndexOutOfBoundsException).
We often think about processing the members in a String using the same techniques (a for loop) as when processing members in an array. For example, here is a typical loop for processing all the characters a String: it adds up the ASCII values of all the characters. 
  String s = Prompt.forString("Enter Name");
  int asciiCharSum = 0;
  for (int i=0; i<s.length(); i++)
     asciiCharSum += s.charAt(i);  //Implicit conversion char->int
  System.out.println(s +"'s ASCII sum = " + asciiCharSum);
Hand simulate this code with the input HOLYBIBLE or al gore.
Array Methods It is often convenient to move array processing operations into methods. In this section, we will show how to write public static methods that process arrays (we can put such methods in our application, or in a library class); then we will exame non-static methods for processing arrays that are stored as instance variables.

The first method finds and returns the lowest index that stores the String value specified by the second parameter. Note the form of the parameter variable for the array: it is the same as declaring a local variable of the String[] type. 

  public static int findLowestIndexOf(String[] a, String value)
  {
    for (int i=0; i<a.length; i++)
      if (a[i].equals(value))
        return i;

    return -1;
  }
Here the code immediately returns the value stored in i if it finds an i such that a[i] stores the same (.equals) String as value; there is no reason to search any further. By standard convention, returning -1 means value was not found in a (since -1 is NEVER a legal index in an array). This method returns -1 only after it discovers that no member in the array store value. Note the use of two return statements, which I believe simplify this code (don't agree? try writing this method with only one return and show it to me if it is simpler).

The next method returns whether every member in the array stores 0. It has a similar test/return structure as findLowestIndexOf. 

  public static boolean all0(int[] a)
  {
    for (int i=0; i<a.length; i++)
      if (a[i] != 0)
        return false;

    return true;
  }
Here the code immediately returns false as soon as it finds a non-0 member in the array (there is no reason to search any further). This method returns true only after it discovers that every member in the array does store a 0.

I often see beginners write such code as follows. This code is more complicated and slower than the code above: it is terrible. If you want to be a programmer, avoid overly complicated and slow code. 

  public static boolean all0(int[] a)
  {
    int count0s = 0;                     //terrible code
    for (int i=0; i<a.length; i++)       //terrible code
      if (a[i] == 0)                     //terrible code
        count0s++;                       //terrible code
                                         //terrible code
    if (count0s == a.length)             //terrible code
      return true;                       //terrible code
    else                                 //terrible code
      return false;                      //terrible code
  }

The next method determines whether an array is stored in increasing order (technically, non-decreasing order, because we ensure only that a subsequent value is no smaller than -at least as big as- the preceeding one). Note the interesting for loop bounds, and the interesting use of the index in the body of the loop. If an array stores N values, we must compare N-1 pairs of values to compute this answer. For the first iteration, we are comparing a[0]>a[1]; for the last iteration we care comparing a[a.length-2] > a[a.length-1], which is comparing the next-to highest index with the highest one in the array. 

  public static boolean increasing(int[] a)
  {
    for (int i=0; i<a.length-1; i++)
      if (a[i] > a[i+1])
        return false;

    return true;
  }
Here the code immediately returns false as soon as it finds a member in the array that is followed by a smaller value (there is no reason to search any further). This method returns true only after it discovers that every member (but the last) in the array is followed by a value that is at least as big.

The following three-parameter method swaps the values in positions i and j in array a. 

  public static void swap(int i, int j, int[] a)
  {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
We can illustrate an example of a call to this method using the following call frame.

  Notice that this method changes the state of the array object whose reference it is passed. The argument x still refers to the same object (the method cannot change what object it refers to), but the state of that object has been changed inside the method.

Finally, here is an interesting method: interesting because it returns a new array object. The lengthAtLeast method takes a String[] as a parameter and returns another String[] as a result: the returned result contains only those Strings from the parameter array that are at least n characters long (specified by the second parameter). 

  public static String[] lengthAtLeast(String[] a, int n)
  {
    int answerLength = 0;
    for (int i=0; i<a.length; i++)
      if (a[i].length() > n)
        answerLength++;

    String[] answer  = new String[answerLength];
    int      answerI = 0;
    for (int i=0; i<a.length; i++)
      if (a[i].length() > n)
        answer[answerI++];

    return answer;
  }
This method works by first determining how many values must be returned. Then it declares an array with exactly that length. Next it fills the array with the required values: notice how the postfix ++ operator returns as a result the original value of answerI but also increments it for the next interation. Finally the method returns the new array it constructed and filled.

Assume that we declare 

 String[] s = new String[]{"a", "ab", "abc", abcd", "abcde"}
We can then write String[] special = lengthAtLeast(s,3); or even s = lengthAtLeast(s,3); if we never need to access the original array object (making s now refer to the one lengthAtLeast constructed.
Arrays Instance Variables We can also write classes that define arrays for their instance variables, constructors that intialize them, and methods that process these intialized instance variables. In fact, the DiceEnsemble class (not SimpleDiceEnsemble) does extactly this. It defines just three instance variables: 
  private int   sidesPerDie;
  private int   rollCount;
  private int[] pips;
 Here, the pips array stores the number of pips showing on each of the dice in the ensemble. Recall from our original pictures (which will now make more sense, because we know about array objects) that we illustrated the declaration of 
  DiceEnsemble d1 = new DiceEnsemble(2,6);
 by

  The constructor for this class reinitializes sidesPerDie and pips (rollCount is declared to store 0). 
  public DiceEnsemble (int numberOfDice, int sidesPerDie)
    throws IllegalArgumentException
  {
    if (numberOfDice < 1)
      throw new IllegalArgumentException
        ("DiceEnsemble constructor: Number of dice ("+numberOfDice+") < 1"); 
    if (sidesPerDie < 1)
      throw new IllegalArgumentException
        ("DiceEnsemble constructor: Sides per die ("+sidesPerDie+") < 1"); 

    this.sidesPerDie  = sidesPerDie;
    this.pips         = new int[numberOfDice];
    //No name conflict for pips; we could write: pips = new int[numberOfDice]
  }
 which reinitializes the instance variable sidesPerDie with the value of the second parameter and reinitializes the instance variable pips (by using the first parameter) to refer to an array that is exactly the right length to contain values for each of the dice in the ensemble. Once these instance variables are initialized, the getNumberOfDice method becomes just 
  public int getNumberOfDice ()
  {return pips.length;}
 So, there is no need to use another instance variable to store the number of dice; that information is already stored in -and can be accessed via- the public final int length instance variable of the pips array.

Likewise, the roll mutator/command becomes simply needs to increment rollCount and fill in every member in the array to which pip refers with new and random pip values for the dice. 

  public DiceEnsemble roll ()
  {
    rollCount++;
    for (int i=0; i<pips.length; i++)
      pips[i]  = (int)Math.round(Math.random()*sidesPerDie + .5); 
    return this;
  }
Many other methods use the pip array to compute their results. After roll has stored new pips, the getPipSum method becomes just 
  public int getPipSum ()
    throws IllegalStateException
  {
    if (rollCount == 0)
      throw new IllegalStateException
        ("getPipSum called, but dice not rolled");

    int pipSum = 0;
    for (int i=0; i<pips.length; i++)
      pipSum += pips[i];
    return pipSum;
  }
 which adds up all the values in the pips array. Notice that this method declares a local variable pipSum. Why is this not declared as an instance variable? Because this information is used only while the method is executing; after that, its values can be forgotten, therefore there is no need to store it as an instance variable. Generally, if a variable can be declared locally instead of as an instance variables, that is to be preferred.

Finally, the getPips method is also simple, but a bit subtle. 

  public int getPips (int dieIndex)
     throws IllegalStateException, IllegalArgumentException
  {
    if (rollCount == 0)
      throw new IllegalStateException
       ("getPip called, but dice not rolled");

    if (dieIndex < 1 || dieIndex > pips.length)
      throw new IllegalStateException
        ("getPip called, but dieIndex("+dieIndex+
         ") is not in the range [1,"+pips.length+"]");

    return pips[dieIndex-1];
  }
It first checks for either no rolls or a dieIndex that is not legal; it is not in the range [1..number of dice]; in either case, it throws an exception. Otherwise it returns the pips showing on the die specified by dieIndex: die 1 is stored in array index 0, die 2 is stored in array index 1, etc.; which is why the subtraction occurs in the index calculation.

So, it is easy to declare array instance variables in classes, initialize them in constructors, and manipulate them in non-static methods. I recommend that you examine how the other methods in the DiceEnsemble class work with the pips array instance variable.

Arrays and the Debugger The Eclipse debugger easily displays arrays in the Variables pane. Recall that the disclosure box in the debugger allows us to observe each instance variable in an object; for arrays it displays each index and the indexed member stored in the array. Surprisingly, the debugger doesn't display the length instance variable, but we can infer its value from the index of the last member shown.

As with any object, the array's indexed members are available by clicking on the disclosure box (plus sign); doing so changes the contents of this box (to minus sign) and discloses the indexes and their members in the array. Of course, if the array members themselves refer to objects, they too will have their own disclosure boxes, which we can click to disclose further information about these objects.

The sample program declares 

  int   howBig = Prompt.forInt("Enter length for the array");
  int[] a      = new int[howBig];
If we enter 5 at the prompt, the Variables pane in the debugger shows

Note that a is not yet shown, because it has not been declared. After a's declaration is executed, the debugger shows

Now a appears; its value shows as int[5], which means a five element int array. Ignor the id part of the value. If we click the disclosure box (plus sign), it changes into a minus sign, and discloses all the indexes and their members in the array.

Here all the array values are shown to store zero initially, because that is the default for int instance variables, and the members of arrays are much like these. After prompting the user for a new value to store in each index (I entered 3, 8, 12, -5, 7), the debugger shows

These values are all highlighted in yellow, because I set a breakpoint after the entire input loop, executing it completely before the debugger stops. Run the Array Demonstration application and familiarize yourself with the operation of the debugger for programs declaring arrays.

Arrays and Classes for Modeling Data Finally, arrays and classes act together synergistically. A class is a heterogeneous data type: it defines any number of instance variables, each declared with its own individual name to store a different type of value. An array is a homogeneous data type: it defines one name storing an arbitrary number of indexed values, all declared to store the same type of value.

Combinations of arrays and classes have all the descriptive power that we need to model almost any kind of information in the computer. As the semester progresses, we will see more sophisticated uses of arrays and classes combined: e.g., an array where each of its members is an object from a class (and inside each object in the class is an instance variable in which an array of other values is stored).

Before continuing with our discussion of arrays as instance variables in collection classes, we take short detour to discuss four related topics: wrapper classes, the Object class, the instanceof operator, and reference casting.

Wrapper Classes Java provides four wrapper classes, one for each of the four primitive types in Java. Their names are Integer, Double, Character, and Boolean (note the standard capitalization for class names). All these classes are defined in the java.lang package. The main purpose of each wrapper class is to be able represent a primitive value as an object: one that contains just that primitive value as its state. Each class has a constructor whose parameter is a primtive; each has a method that returns the value of the primitive stored in the constructed object (intValue, doubleValue, charValue, and booleanValue name these methods respectively). Objects of these classes are immutable, so once an object is constructed the primitive it stores never changes. Examine the Javadoc pages for these wrapper classes; observe their many constructors and methods (all accessors/queries).

So, for example, we can define Integer x = new Integer(10); the variables x now stores a reference to an object constructed from the Integer class whose state is 10. We cannot write x+1 because x is not an int but is an Integer, and there is no prototype for + that adds an Integer to an int. But, we can write x.intValue() + 1 because the intValue method returns an int: the one stored in the object x refers to.

Because wrapper classes are immutable, there is no way to increment the primitive value that is stored in the object x refers to. But, we could write x = new Integer(x.intValue()+1) whose execution is illustrated below.

  After executing this statement, the value in the object x refers to is one bigger: but instead of changing the state of the original object, x now refers to a different one. When we discuss increasing the length of an array, we will see a similar solution.

Wrapper classes also define various other useful information (and sometimes, quite a lot). For example, we have seen that the Integer class stores the static final int values MIN_VALUE and MAX_VALUE; it also stores the static int method parse): e.g., int i = Integer.parse("123");

From what we know of Java so far, there is no reason to use wrapper classes! But, we are about to explore two simple but general collections, stack and queue, which can store only references to objects, and not primitives. In this context, if we want to store a primitive value in such collections, we must first wrap it in an object (using a constructor of the appropriate wrapper class), and store a reference to that object in the collection.

The Object Class The Object class in Java is a very special class. When we learn about inheritance hierarchies, we will see that this class is special because it is at the root of the inheritance hierarchy: every class in Java is an extension/specialization of the Object class. (You can see this trivially if you look at the Javadoc for any other class: it will always show java.lang.Object as the first class in the hierarchy.) This class is defined in the java.lang package. For now, though, we will concentrate on just two salient facts about the Object class, discussed below.

We can specify Object as the type of a variable: this includes local variables, parameter variables, instance variables -and now, even the type stored as the indexed members in array variables. If we declare a variable to be of the Object type...

  1. The variable can store a reference to an object constructed from any class.
  2. The only methods that we can call on the variable are those methods defined in the Object class.
We have always spoken of a reference variable storing a reference to a object constructed from a compatible class: up to now, this has always meant "constructed from the same class": e.g., Java ALLOWS Timer t = new Timer(); but DOES NOT ALLOW Timer t = new Rational(1,2); Now, we see from the rule above that a variable declared to be of type Object can store any reference, because any reference is compatible with Object.

So, Java ALLOWS Object o = new Object(); and Object o = new Timer(); and Object o = new Rational(1,2); Note, though, that we still cannot store a value of a primitive type in such a variable: e.g., Java DOES NOT ALLOW Object o = 10; because it must store a reference value, not a primitive value. But remember that we can use wrapper classes to achieve an equivalent result: e.g., Java allows Object o = new Integer(10);

The Object class defines only about a dozen methods, of which toString is the only one that we have studied. Thus, Java allows calling o.toString() regardless of which ALLOWABLE declaration above we use. Regardless of what kind of object the reference in an Object variable refers to, we can call only Object methods on it. So, even if we wrote Object o = new Integer(10); Java DOES NOT ALLOW calling o.intValue() because intValue is not a method defined in the Object class.

Thus, using the type Object gives us power in one dimension but restricts power in another. It is powerful because variables of this type can store (generic) references to any objects. But, it restricts us from calling all but a few methods on these variables. This balance of power will be explored throughout the rest of this lecture and addressed later, as the basis of inheritance hierarchies and polymorphic behavior.

There is an important distinction between the declared type of a variable and the class of the object to which it refers. There was no distinction before, because the type of a variable and the class of the object to which it refers were always the same. What seems like a small leak in this rule will turn into a mighty river as we discuss interfaces and inheritance hierarchies.

The instanceof operator We have learned that variables declared of type Object can store references to objects constructed from any class. Java provides a way for us to check whether a reference refers to an instance of a specified class. The instanceof operator (one of two operators in the Java that are also keywords) performs this operation, returning a boolean result. Its form of use is x instanceof Integer; it is a binary infix operator whose second operand is the name of a class.

When we learn about reference casting below, we will see statements like 

  if (x instanceof Integer)
  ...do something with x knowing it is a reference to an Integer
Finally, Java considers null to not be an instance of any class (it refers to no instance of a class). So null instanceof C returns false for any class C. Lets summarize our current understanding of the instanceof operator. If r instanceof C returns true it means that r stores a non-null reference to an object constructed from class C; if it returns false it means that either r stores null or it stores a reference to an object constructed from a class other than C.
Reference Casting We have learned that we can store any reference into an Object variable. But once we do so, we can use the Object variable to call only methods defined in the Object class. We will now learn how to tell Java to treat a reference stored in an Object variable just like a reference to the class that the object it refers to was really constructed from (gulp! reread the previous sentence, it it tortuous). This allows us to use Object variables to call all the methods defined in that class of the object to which it refers.. We will discuss this asymmetry in this lecture, and explore it further and deeper in the lectures on inheritance.

Assume that we define Object o = new Integer(10); Java DOES NOT ALLOW us to call o.intValue(); it would detect and report such an error at compile time. But Java DOES ALLOW us to call ((Integer)o).intValue(). Here we are using reference casting to cast o to be a reference to an object of type Integer (which it is) and then we are calling the intValue method on that casted reference. In casting, we always write the type that we are casting TO in parentheses; here we are casting o to be of type Integer. We need the other (outer) parentheses because casting has a lower precedence than member selection (the dot operator), and we want to cast first.

When we cast an Object reference to another class, we are telling the Java compiler to act as though that reference really refers to an object from that class. Afterward, the Java compiler allows us to use the casted reference to call any methods defined in that class. When Java actually runs our code (after the program compiles correctly) it checks each cast: if Java discovers that the cast won't work -that the reference doesn't really refer to an object from the specified class- then it throws the ClassCastException before trying to call the method. Java checks the cast by automatically using the instanceof operator: if the cast (Integer)o appears in our code, Java first checks o instanceof Integer, throwing an exception if this expression evaluates to false. (technically, if o stores null Java throws the NullPointerException before even checking instanceof.)

Thus, even given the declaration Object o = new Integer(10); we could write ((Double)o).doubleValue() in our code. Because o is casted to a Double, the Java compiler allows us to call the doubleValue() method on it. But, whent the program runs, this cast will throw the ClassCastException because the cast fails: when Java checks o instanceof Double this expression evaluates to false.

Thus, we separate our understanding of casting into Compile Time and Run Time components. Assume that we write the cast (C)o in our code.

  • Compile time: Java allows o to be treated as if it refers to an object from class C. Specifically, we can call any methods defined from class C on it.
  • Run time: Java checks the cast to make sure it is correct: that the casted reference really does refer to an object from class C If it does, the code continues executing; if it doesn't, Java throws ClassCastException.
So, a cast is a promise that Java believes while it is compiling the program, but also checks while running the program. It is an excellent example of Reagan's statement about arms reduction treaties with the former Soviet Union: Trust but verify.

We can explicitly use the instanceof operator to ensure that our code will never throw ClassCastException. We can write code like 

  if (o instanceof Integer) {
    Integer i = (Integer)o;
    ...use of i; e.g., i.intValue()
  }
In this code, the cast cannot fail beause the block containing the cast is executed only when the if's test, o instanceof Integer, evaluates to true.

Pragmatically, casting is most often performed by itself in a variable declaration, as illustrated above. As an example, most classes include an equals method that allows comparison with a reference to any object. For example, the Rational class should include an equals method defined by 

  public boolean equals(Object other)
  {
    if ( !(other instanceof Rational) )   //From a different class?
      return false;
    if (other == this)                    //Is the same object?
      return true;                        //  no need to check fields!

    //Cast is guaranteed to work: other is instanceof Rational
    Rational otherRational = (Rational)other;

    //Check State (both fields)
    return this.numerator   == otherRational.numerator &&
           this.denominator == otherRational.denominator;
  }
Most equals methods follow the same three-part strategy:
  1. If the parameter is not a reference to an object of the correct type, it returns false.
  2. If the parameter is == to this, then we are comparing an object to itself, in which case it returns true immediately, without checking the state of the object; we know that any object stores the same state as itself.
  3. Otherwise, it legal to cast the parameter and store it in a local variable of the correct type; once that is done, the states of this object and the other one are compared.
Collection Classes: An Introduction Collection classes manage collections of values. They include methods to add values to the collection, remove values from the collection, and inquire about values in the collection. We use arrays to store these values, and unlike our previous discussion the arrays are not always filled. Generally, a collection class can be represented by two instances variables: one refers an array storing all the values in the collection; the other is an int that keeps track of how many indexed members in the array are actually being used.

In the rest of this lecture we will discuss two simple and well-known collection classes: stack and queue. These classes are useful in many programs that model real-world data and processes. Their definitions will heavily rely on the Object type: both in methods and for array instance variables. Such collections can be used, unchanged, in any programs that we write. This kind of generality and reusability is the holy grail of effective class design.

The stack and queue collections are straightforwad to implement. The straightforward implementation of the stack collection (which implements a last-in/first-out ordering) is efficient. But, the straightforward implementation of the queue collection (which implemements a first-in/first-out ordering) is not efficient; later in the semester we will examine a second, more complicated but efficient implementation of queues. A fundamental component of both implementations is a doubleLength method to increase the length of the array storing the collection.

The SimpleStack and SimpleQueue classes that we cover in this lecture (along with a simple driver application for each), are available online. You can download, unzip, run, and examine all this code in the SimpleStack Demonstration and SimpleQueue Demonstration applications.

Stacks and LIFO We can visualize a stack as a vertical array, whose indexes increase as the array goes upward. The biggest index that stores a non-null reference is known as the top of the stack. Each SimpleStack object stores two instance variables: a reference to such an array and a value top. References are both added (pushed on) and removed (popped off) near the top of the stack; this means that we characterize a stack as Last-In/First-Out: the last reference added to (pushed on) the stack is the first one removed (popped off). Such a stack is declared and initialized simply by SimpleStack x = new SimpleStack(); The following picture shows a stack onto which three strings have been pushed.

  Notice that stack is declared to be of type Object[] so each indexed member can store a reference to any object. Also, we represent null by a slash (/), as appears in array index 3 in the picture above; we will continue to use this graphical notation throughout the rest of the course for null references.

The SimpleStack collection class consists of definitions (elided here, but fully shown in the discussion below) for the following constructors, methods, and fields. 

  //Constructors
  public SimpleStack (int initialSize) throws IllegalArgumentException {...}
  public SimpleStack () {...}

  //Mutators/Commands
  public void    makeEmpty () {...}
  public void    push      (Object o) {...}
  public Object  pop       () throws IllegalStateException {...}
  
  //Accessors/Queries
  public Object  peek      () throws IllegalStateException {...}
  public boolean isEmpty   () {...}
  public int     getSize   () {...}
  public String  toString  () {...}

  //Private (helper) methods
  private void doubleLength() {...}
  
  //Fields (instance variables)
  private Object[] stack;
  private int      top = -1;
Let's explore in detail the implementation of each constructor and method, in terms of how they manipulate the instance variables.
Length Doubling Before looking at all the public constructors and methods, we will examine the private doubleLength method, which is called only in push As we push more values onto a stack, the array storing these values must get bigger. Although the length of an array object cannot be changed once it has been constructed, the doubleLength method does the equivalent by constructing a new, bigger object; we used much the same approach to "increment" a variable refering to an immutable Integer object. Thes code for length doubling is quite simple, but subtle. 
  private void doubleLength ()
  {
    Object[] temp = new Object[stack.length*2];
    for (int i=0; i<stack.length; i++)
      temp[i] = stack[i];
    stack = temp;
  }
 This method is called only when the array object that stack refers to is filled with references. It works in three steps:
  1. It declares the local variable temp and initializes it to refer to a newly constructed array object whose length is twice as big as the length of the array stack refers to. Initially, all indexed members store null.
  2. It copies all the non-null references from stack to temp in order (from 0 up to top).
  3. It makes stack refer to the new object.
Thus, for all intents and purposes, we have doubled the length of stack: it now refers to an array that stores the same values, but whose length (for storing new values) is twice as long. The picture below illustrates how this method executes.

  Notice that top remains unchnaged at 1 because there are still only two references stored in the array (at indexed members 0 and 1). The instance variable stack no longer refers to the old array object, so eventually Java will recycle this object.

Another, similar way to write this method (maybe a bit clearer than using temp) is 

  private void doubleLength ()
  {
    Object[] old = stack;
    stack = new Object[stack.length*2];
    for (int i=0; i<stack.length; i++)
      stack[i] = old[i];
  }

Although this class doesn't define it, I have written the trimLength method below. This method shrinks the array to be just big enough to store all the current references in stack. Here, the first line constructs a "just big enough" array and then the for loop copies all the references into it. 

  private void trimLength()
  {
    Object[] temp = new Object[top+1];
    for (int i=0; i<=top; i++)
      temp[i] = stack[i];
    stack = temp;
  }
We could likewise implement this method with old instead of temp. Note that we could include an if to immediately return if stack.length were equal to top+1, but his code, while redundant, works. If we called x.trimLength() the actions in the picture above would be reversed.
Stack Implementation We will now explore all the public constructors and methods in this class. You are invited to hand simulate this code and draw the relevant pictures to help you better understand it. We start with the definition of the general constructor. 
  public SimpleStack (int initialSize)
    throws IllegalArgumentException
  {
    if (initialSize < 1)
      throw new IllegalArgumentException
        ("SimpleStack Constructor: initialSize("+initialSize+") < 1");

    stack = new Object[initialSize];
  }
 Basically, this constructor verifies the initialSize parameter and then uses it to construct an array that can contain that many references. Recall that when arrays of references are constructed, all indexed members store null. Observe that top is declared to store -1 initially, and no change is made to it here. We say that the stack is empty if it is in this state. In fact, it is a class invariant that there are always top+1 values stored in the stack; so at constuction there are 0 values stored. Another explanation for this intial value will emerge when we study the code for the push method.

The second constructor has no parameter and constructs an array with enough room for just one value. It is written simply as 

  public SimpleStack ()
  {this(1);}
Unless we know something special about how many values we will push on a stack, we will often use this simpler constructor.

The makeEmpty method removes all references from the stack and reinitializes top to -1; so, after this method call the stack is again empty. We define this method, a mutator/command, by 

  public void makeEmpty ()
  {
    for (int i=0; i<=top; i++)
      stack[i] = null;
    top = -1;
  }
To understand this method, hand simulate it in the state illustrated in the picture above. Note that all indexed members greater than top already store null.

The push method, a mutator/command, adds a reference on top of the stack; the reference in its parameter o is stored one beyond the old top of the stack, and becomes the new top of the stack. It first checks to see if there is no more room in the array; if so, it doubles the length of the array as described above. Then it always increments top and stores the reference o at this new index in the array (there will always be room to store it). 

  public void push (Object o)
  {
    if ( getSize() == stack.length)
      doubleLength();
        
    top++;
    stack[top] = o;        //or just stack[++top] = o;
  }
Notice that a newly constructed SimpleStack stores -1 in top; the first time that this method is called it increments that value to 0 and then stores the parameter into the array at index 0. Notice that the if calls getSize to check whether there is not enough room for the new reference on the stack (we can worry about the details of this method later). Finally, notice that the semantics of the prefix operator ++ allows us to perform both state changes in a single statements: stack[++top] = o;

Because its parameter type is Object, we can call push with any argument that refers to an object. In fact, we can easily push different classes of objects onto the same stack, as illustrated below.

  The pop method, a mutator/command and accessor/queury, returns a reference to the object currently at the top of the stack, and it also removes that reference from the stack (replacing it by null); the value underneath it becomes the new top of the stack. Of course, if the stack is empty when this method is called, it throws IllegalStateException (the stack is in an illegal state to perform the pop operation). This code is written as 
  public Object pop () throws IllegalStateException
  {
    if ( isEmpty() )
      throw new IllegalStateException
        ("SimpleStack pop: Stack is empty");
    
    Object answer = stack[top];
    stack[top] = null;
    top--;                       //or just stack[top--] = null;
    return answer;
  }
Notice how the reference at the top of the stack is stored in the local variable answer; then the old indexed member is set to null and top is decremented; then the stored answer is returned. Notice that the if calls isEmpty to check whether there is no value on the stack to be popped (we can worry about the details of this method later). Finally, notice that the semantics of the postfix operator -- allows us to perform both state changes in a single statement: stack[top--] = null;

Notice that the pop method returns a reference of type Object. Recall that this means that the reference returned can refer to an object from any class. Obviously we can write Object o = x.pop(); to store this reference, but we cannot do anything interesting with o (only call methods on it that are defined in the Object class). But, if we know the reference is to a String object, we can instead write String s = (String)x.pop(); The cast here is mandatory, otherwise the Java compiler will detect and report an error. Recall that the member selector operator (the dot) has precedence over the cast; in this statement we want to apply the cast last, so we need no extra grouping parentheses.

Finally, note the asymmetry: we can call push without casting (any argument reference stored to an Object parameter works); but when we call pop, we must cast the reference to do anything useful with it. Another way of saying this: putting a reference in a stack hides its type; when taking a reference out of a stack its type must be restored with a cast. Of course, we can check its type with the instanceof operator.

Similarly, the peek, an accessor/query, returns the reference currently at the top of the stack (like pop) but it DOES NOT remove it (unlike pop). 

  public Object peek () throws IllegalStateException
  {
    if ( isEmpty() )
      throw new IllegalStateException("SimpleStack pop: Stack is empty");
    
    return stack[top];
  }
The isEmpty accessory/query, used in pop and peek, returns whether or not the stack is empty. It is written simply as 
  public boolean isEmpty ()
  {return top == -1;}
 Recall that in an empty stack, top stores -1. Another way to implement this method would be return getSize() == 0;

The getSize accessory/query, returns the number of references on the stack. It is written simply as 

  public int getSize ()
  {return top+1;}
Recall that in an empty stack, top stores -1; in this case the value getSize returns is 0. Recall that there is a class invariant that states there are always top+1 values stored in the stack.

Finally, the toString method returns the value of top, the length of the stack array, and the String values of all the references in the stack. It uses lots of catenation to get the job done. 

  public String toString ()
  {
    String answer = "SimpleStack[top="+top+"/length="+stack.length;
    for (int i=0; i<=top; i++)
      answer += ";stack["+i+"]="+stack[i];
    answer +=  "]";
    
    return answer;
  }

In summary: Each SimpleStack stores the stack array (storing the references in the stack) and top (storing the index of the last reference). Generally, push increments top by 1 and pop decrements top by 1. So that the first push (or any push on an empty stack) stores its reference in index 0. The number of references in the stack is always top+1; an empty stack stores 0 references so top in an empty stack must be -1. The size of the array is doubled when necessary (and it never shrinks).

Stacks are famous in Computer Science, because method calls are implements via stacks. When a method is called, it call frame (or the computer equivalent) is pushed onto the call stack. This is the same call stack that appears in a pane in the debugger (although it grows from the top downward). Each call to a method pushes that method onto the call stack; each return from a method pops that method off the call stack (returning to execute code at the new method on top of the call stack -the one that called the method that just returned). In fact, stacks are so common in computing (see the next section too) most computers have special instructions that push/pop a value onto/from a hardware stack.

A Stack Application: RPN and Stacks We should now all masters of writing formulas as expressions in Java, and analyzing such expressions: we know about the precedence of operators, parentheses to override precedence, and left to right (or right to left) associativity. But now we ask the question, "Is that the simplest way to write expressions". The answer is no. In this section we shall discuss a simpler notation for writing expressions, and its relationship to stacks (which we use to evaluate such expressions easily).

The notation that we will learn to write expressions is called Reverse Polish Notation (RPN). The original Polish Notation was invented by a group of famous Polish logicians in the late 1930s. They wanted to prove things about expressions, and therefore wanted to invent the simplest rules possible to write arbitrary expressions. This group was wiped out in World War II, and the notation was rediscovered in the 1960s and used in the LISP programming language; many calculators also use RPN (as well as the programming language Forth). In Polish Notation, operators always appear before their operands; in RPN, operators always appear after their operands.

RPN is very simple: it has no operator precedence, no associativity rules, and no parentheses to override precedence and associativity rules! We evaluate an RPN expression (using oval diagrams) in a very straighforward manner, scanning it from left to right (we will ignore types here, and concetrate on values).

  1. If the next token is a number, circle it, and write its value below.
  2. If the next token is an operator, use one big circle to enclose the operator and its operands (for binary operators, the two previous circles, however big they are), apply the operator to these operands, and write the resulting value below the big circle.
Here are some examples that illustrate Java expressions and their equivalent RPN.

JavaRPN 
1 + 2 * 3
1 2 3 * +
 
(1 + 2) * 3
1 2 + 3 *
 
(1 + 2) * ((3 + 4) * (5 + 6))
1 2 + 3 4 + 5 6 + * *

Note that one property of Java and RPN expressions is that the operands appear in the same order; the earlier an operator is applied in the Java expression (using all the complicated rules) the earlier it appears in RPN. Here is a picture illustrating the evaluation process for expressions written in RPN.

  We can use a stack to evaluate an expression written in RPN simply. We translate the circling rules into
  1. If the next token is a number, push it on the stack.
  2. If the next token is an operator, pop the top two numbers off the stack, apply the operator to these values, and push the result value back on the stack.
We can translate this algorithm to use a StringTokenizer to get all the tokens and a SimpleStack (always containing objects from the Integer wrapper class) to perform the computation. For example, if the operator were a plus, then we translate the second rule into the following code (note the casting). 
  Integer operand2 = (Integer)x.pop();
  Integer operand1 = (Integer)x.pop();
  x.push ( new Integer (operand1.intValue() * operand2.intValue()) );
 For non-commutative operators (- and /) we must realize the the second/right operand is on the top of the stack and the first/left operand is underneath it.

Here is a picture illustrating the evaluation process of the largest expression.

  The RPN Calculator project uses the StringTokenizer and SimpleStack classes to implement the calculator. In fact, this project also contains two other application programs. The first uses the BigInteger class instead of the Integer wrapper class The second allows relational and logical operators as well, pushing/popping references to both the Integer and Boolean wrapper classes. The operator determines how to cast the references popped off: Boolean for the operators !, &&, and ||; Integer for the arithmetic and relation operators.
Queues and FIFO We can visualize a queue as a horizontal array, whose indexes increase as the array goes rightward. The biggest index that stores a non-null reference is known as the rear of the queue. Each SimpleQueue object stores two instance variables: a reference to such an array and a value rear. References are added (enqueued) at the rear of the queue and removed (dequeued) from the front of the queue (always index 0); this means that we characterize a queue as First-In/First-Out: the first reference added to the queue is also the first one removed.

Thus, a queue implements a "fair" line, where the first person getting into the line is the first person leaving the line to be served (with the others getting in line behind him/her). In fact, in England, people "queue up" to stand in a "queue" (just as we "line up" to stand in a "line"). Such a queue is declared and initialized simply by SimpleQueue x = new SimpleQueue(); The following picture shows a queue into which three strings have been enqueued.

  Notice that q is declared to be of type Object[] so each indexed member can store a reference to any object. Also, we represent null by a slash (/), as appears in array index 3 in the picture above; we will continue to use this graphically notation throughout the rest of the course.

If we call dequeue to return and remove the first value, the new picture becomes

  The SimpleQueue collection class consists of definitions (elided here, but fully shown in the discussion below) for the following constructors, methods and fields. 
  public SimpleQueue (int initialSize) throws IllegalArgumentException {...}
  public SimpleQueue () {...}

  //Mutators/Commands
  public void    makeEmpty () {...}
  public void    enqueue   (Object o) {...}
  public Object  dequeue   () throws IllegalStateException {...}
  
  //Accessors/Queries
  public Object  peek      () throws IllegalStateException {...}
  public boolean isEmpty   () {...}
  public int     getSize   () {...}
  public String  toString  () {...}
 
  //Private (helper) methods
  private void doubleLength() {...}
  
  //Fields (instance variables)
  private Object[] q;
  private int      rear;
Let's explore in detail the implementation of each constructor and method, in terms of how they manipulate the instance variables. The doubleLength method in this class is almost identical to the one we discussed in SimpleStack, but it refers to the instance variable q. Again, this method is called only when the array object that q refers to is filled with non-null references. 
  private void doubleLength ()
  {
    Object[] temp = new Object[q.length*2];
    for (int i=0; i<q.length; i++)
      temp[i] = q[i];
    q = temp;
  }
Queue Implementation We now will explore all the public constructors and methods in this class. You are invited to hand simulate this code and draw the relevant pictures to help you better understand it. Most of these definitions are similar to those in the SimpleStack class; pop and dequeue are most different, implementing the last-in/first-out and first-in/first-out difference. So, make sure you read the description of this method carefully. We start with the definition of the general constructor. 
  public SimpleQueue (int initialSize)
    throws IllegalArgumentException
  {
    if (initialSize < 1)
      throw new IllegalArgumentException
         ("SimpleQueue Constructor: initialSize("+initialSize+") < 1");

    q = new Object[initialSize];
  }
 Basically, this constructor verifies the initialSize parameter and then uses it to construct an array that can contain that many references. Recall that when arrays of references are constructed, all indexed members store null. Observe that rear is declared to store -1 initially, and no change is made to it here. We say that the queue is empty if it is in this state. In fact, it is a class invariant that there are always rear+1 values stored in the queue; so at constuction there are 0 values stored. Another explanation for this intial value will emerge when we study the code for the enqueue method.

The second constructor has no parameter and constructs an array with enough room for just one value. It is written simply as 

  public SimpleQueue ()
  {this(1);}
Unless we know something special about how many values we will enequeue in a queue, we will often use this simpler constructor.

The makeEmpty method removes all references from the queue and reinitializes rear to -1; so, after this method call the queue is again empty. We define this method, a mutator/command, by 

  public void makeEmpty ()
  {
    for (int i=0; i<=top; i++)
      q[i] = null;
    rear = -1;
  }
To understand this method, hand simulate it in the state illustrated in the picture above. Note that all indexed members greater than rear already store null.

The enqueue method, a mutator/command, adds a reference to the rear of the queue; the reference in its parameter o is stored one beyond the old rear of the queue, and becomes the new rear of the queue. It first checks to see if there is no more room in the array; if so, it doubles the length of the array as described above. Then it always increments rear and stores the reference o at this new index in the array (there will always be room to store it). 

  public void enqueue (Object o)
  {
    if ( getSize() == q.length)
      doubleLength();
        
    rear++;
    q[rear] = o;        //or just q[++rear] = o;
  }
Notice that a newly constructed SimpleQueue stores -1 in rear; the first time that this method is called it increments that value to 0 and then stores the parameter into the array at index 0. Notice that the if calls getSize to check whether there is not enough room for the new reference in the queue (we can worry about the details of this method later). Finally, notice that the semantics of the prefix operator ++ allows us to perform both state changes in a single statements: q[++rear] = o;

Because its parameter type is Object, we can call enqueue with any argument that refers to an object.

The dequeue method, a mutator/command and accessor/queury, returns a reference to the object currently at the front of the queue, and it also removes that reference from the queue by shifting all remaining values in the array left (towards the front) by one index position; this leaves duplicate references in q[rear-1] and q[rear], so the last one is replaced by null). Of course, if the queue is empty when this method is called, it throws IllegalStateException (the queuen is in an illegal state to perform the dequeue operation). This code is written as 

    public Object dequeue () throws IllegalStateException
  {
    if ( isEmpty() )
      throw new IllegalStateException
        ("SimpleQueue dequeue: queue is empty");
    
    Object answer = q[0];
    
    //Shift all remaining values (q[1..rear]) left by 1 index, into
    //  positions  q[0..rear-1]
    for (int i=0; i<rear; i++)
      q[i] = q[i+1];
   
    //Remove duplicate in q[rear]; it has been copied into
    //  q[rear-1] too 
    q[rear] = null;
    rear--;                 //or just q[rear--] = null;
    return answer;
  }
Notice that the if calls isEmpty to check whether there is no value on the queue to be dequeued (we can worry about the details of this method later). Finally, note that the semantics of the postfix operator -- allows us to perform both state changes in a single statement: q[rear--] = null;

This method is much different than the pop method for stacks, because it requires a for loo to examine every value in the array (as do the makeEmpty and toString methods in both classes). Thus, the amount of time that it takes to dequeue a value is dependent on the number of values already stored in the queue. This inefficiency can be eliminated by a more complicated class that implements a queue: we will discuss it later in the semester.

Similarly, the peek, an accessor/query, returns the reference currently at the front of the queue (like dequeue) but it DOES NOT remove it (unlike dequeue). 

  public Object peek ()
    throws IllegalStateException
  {
    if ( isEmpty() )
      throw new IllegalStateException
        ("SimpleQueue peek: queue is empty");
    
    return q[0];  
  }
The isEmpty accessory/query, used in dequeue and peek, returns whether or not the queue is empty. It is written simply as 
  public boolean isEmpty ()
  {return rear == -1;}
 Recall that in an empty queue, rear stores -1. Another way to implement this method would be return getSize() == 0.

The getSize accessory/query, returns the number of references on the queue. It is written simply as 

  public int getSize ()
  {return rear+1;}
Recall that in an empty queue, rear stores -1; in this case the value getSize returns is 0. Recall that there is a class invariant that states there are always rear+1 values stored in the queue.

Finally, the toString method returns the value of rear, the length of the q array, and the String values of all the references in the queue. It uses lots of catenation to get the job done. 

  public String toString ()
  {
    String answer = "SimpleQueue[rear="+rear+"/length="+q.length;
    for (int i=0; i<=rear; i++)
      answer += ";q["+i+"]="+q[i];
    answer +=  "]";
    
    return answer;
  }

In summary: Each SimpleQueue stores the q array (storing the references in the queue) and rear (storing the index of the last reference). Generally, enequeue increments rear by 1 and dequeue decrements rear by 1. So that the first enqueue (or any enqueue on an empty queue) stores its reference in index 0. The number of references in the queue is always rear+1; an empty queue stores 0 references so rear in an empty queue must be -1. The size of the array is doubled when necessary (and it never shrinks).

A typical use of queues is in simulating systems where entities move from one part of the system to another, in a fixed order. For example, we might want to simulate a supermarket by getting data on when a customer enters, how long the customer shops in the store, how many items the customer buys, and how long it takes the customer to checkout (once he/she reaches the front of the checkout line). The only remaining piece of information missing is how long the customer waits in the checkout line. We can use queues (operating on this data) to simulate a variety of cash register configurations: some registers may restrict the number of items checked through. Then we can determine whether certain configurations are better than others (in terms of customer throughput).

Length Doubling: Performance Analysis Before finishing this lecture, we should do a short performance analysis of why doubling the length of an expanding stack/queue is a good strategy (say, compared to expanding it by increasing its length just by one). If we always expand the length of the array by one -the amount needed to store the new value, we would still be required to copy all the values each time we construct a new array. But, if we double the length of the array, we can put many new values into it without having to expand it and copy values.

For the analysis below, assume that a program reads from a file and pushes each value onto the top of a stack. For example, if we are reading 1,024 (210) values from a file and pushing them onto the top of a stack; further assume that the stack is initially constructed to refer to an array of length 1.

If we expand the length by just one, we will have to call the expand method 999 times. The first time requires copying 1 value, the next time 2 values, the next time 3 values, ... and the final time 1023 values. The total amount of copying is 1+2+...+1023 which is 523,776 copying operations! The general formula for 1+2+...+n is n(n+1)/2; os the number of copying operations grows as the square of the number of values we push.

Now let's analyze the doubling approach. The first time requires copying 1 value, the next time 2 values, the next time 4 values, and the final time 512 values (when increasing the array from length 512 to length 1024). The total amount of copying is 1+2+4+8+16+32+64+128+256+512 which is only 1,023 copying operations (over 500 times fewer than the previous method): so, if this method takes .1 second, the previous method almost takes a minute! If n is some power of 2, the formula for 1+2+4+...+n is 2n-1.

Thus, to push n values onto the top of a stack we must double the array only about Log2(n) times; note that logarithm (base 2) is a very slowly growing function: Log2(1,000) is 10; Log2(1,000,000) is 20; and Log2(1,000,000,000) is 30.

Of course, in the first approach, the array is always exactly the right size. With the second approach, we would have to call some kind of trim method to reduce it to exactly the right size. This would require copying every value again. In the previous example, it would require a total of 2,047 copy operations (still over 250 times faster than the first method). The exact formula is n+2Log2(n)+1 -1.

The bigger the data file, the more efficient the doubling method is. For 1,000,000 values, the first method requires about 500,000,000,000 (500 billion) copy operations; the doubling method requires only about 3,000,000 (three millon) copy operations: that makes it 166,666 times faster).

When we formally study the Analysis of Algorithms we will perform more analyses like these for methods defined in collection classes.

Problem Set To ensure that you understand all the material in this lecture, please solve the the announced problems after you read the lecture.

If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a CA, or any other student.

  1. Write a method namd countOccurence that counts and returns how often a value (specified by an int parameter) occurs in an array (specified by an int[] parameter).

  2. Explain why the following code does not always compute the correct result; under what circumstances does it compute the correct result? 
      public static boolean all0(int[] a)
{
  for (int i=0; i<a.length; i++)
    if (a[i] != 0)
      return false;
    else
      return true;
}

  3. What happens to array a if swap is called with the same value for i and j: e.g.,a.swap(3,3);?

  4. Write a method name reverse which reverses the order of it int array parameter (calling reverse twice results in the original array ordering).

  5. Write a method name circularShiftLeft which shifts every value in its int[] parameter to the left by one index, placing the value at index 0 into the last index.

  6. Write a method name circularShiftRight which shifts every value in its int[] parameter to the right by one index, placing the value at the last index into index 0.

  7. Write a swap method for arrays of String. Draw a method call and its call frame to illustrate what happens when the first and last index values are swapped (swap(s,0,s.length-1)).

  8. After class one day, a very clever student showed me the following code as an alternative to the increasing method discussed above. He asserted that it worked correctly. Note that this code inverts the loop continuation and if test. I blanched, because the for loop looks very different from the ones that I am used to analyzing; but then I went ahead and analyzed the code (by rapidly doing some hand simulations in my brain). Does this code always, sometimes, or never work correctly? Hint, try some hand simulation on normal and boundary cases. If it only works sometimes, for which arrays does it produce correct and incorrect answers. 
      public static boolean increasing(int[] a)
  {
    for (int i=0; a[i]<=a[i+1]; i++)
      if (i+1 == a.length-1)
        return true;

    return false;
  }

  9. Assume we declare SimpleStack s = new SimpleStack();. Does Java allow us to write, s.push(null); If it is not allowed, explain why not; if it is allowed, explain what happens.

  10. Assume we declare SimpleStack s = new SimpleStack(); and push some values onto the stack. Does Java allow us to write, System.out.println( s.pop() ); If it is not allowed, explain why not; if it is allowed, explain what happens.

  11. Assume we declare SimpleStack s = new SimpleStack(); and push some values onto the stack.
    • Explain why we cannot use the following cascaded method calls to empty the stack and push two values onto it: s.makeEmpty().push("a").push("b"); What changes could we make to these methods to allow such a cascaded method call.
    • Explain why we cannot use the following cascaded method calls to retrieve the value under the top of the stack: Object o = s.pop().pop();

  12. Explain why the following implementation of the pop method works correctly; notice that it use a try-finally combination with no local variable answer. 
      public Object pop () throws IllegalStateException
  {
    if ( isEmpty() )
      throw new IllegalStateException
        ("SimpleStack pop: Stack is empty");
    
    try{
      return stack[top];
    }finally{
      stack[top] = null;
      top--;                       //or just stack[top--] = null;
    }
  }

  13. Copying the form of the equals method in the Rational class (see the bottom of the Reference Casting section), write an equals method for SimpleStack or SimpleQueue Include all state criteria that you think is relevant.

  14. How could we change the SimpleQueue class to disallow enqueueing null references, either by not modifying the array and returning immediately, or by throwing an IllegalArgumentException.