| Introduction |
In this lecture we will continue our study of self-referential data structures
by examining graphs.
Like linked lists and trees, graphs contain nodes: these nodes are objects
instantiated from a class that contains instance variables that refer to
other nodes from this same class.
In some sense, graphs are very easy to specify because, unlike linked lists and
trees, there are no restrictions: any node can refer to any other node.
In fact, we can define a linear linked list as a restricted graph: all nodes have an in-degree and out-degree of 1 (except the first has an in-degree 0 and the last has out-degree of 0); trees can be similarly defined in terms of a restricted graph: an acyclic graph in which every modes has in-degree of 1 (except the first which has an in-degree of 0). Both cycles and in-dgree are technical terms defined below). Here is a picture of a DAG (directed acyclic graph) which is halfway between a tree (it has no cycles) and a graph (but it has a node with in-degree two: the common subexpression). |

| We can use graphs to model very many real-world relationships. Then, we can use standard graph algorithms to process the graph, producing answers to problems modeled via graphs. There are entire books written on graph algorithms. We will examine a few interesting graph algorithms (again concentrating on the algorithms themselves, not the methods that implement them) in this lecture and the next one. |
| Terminology |
The mathematical theory of graphs was first developed by the famous
mathematician Leonard Euler in 1735.
It was motivated by a desire to solve the following problem (taken from the
web page
The Beginning of Topology,
which also contains Euler's solution to this problem).
|

Euler proved that no such tour (now called an Euler path) was possible
(a similar problem is known as "The Traveling Salesman" problem, in which
the traveler must end up at the same place he started; it also involves
another criteria: minmizing the distance traveled)
Using some of the terminology we will learn below, the relevant theorems are:
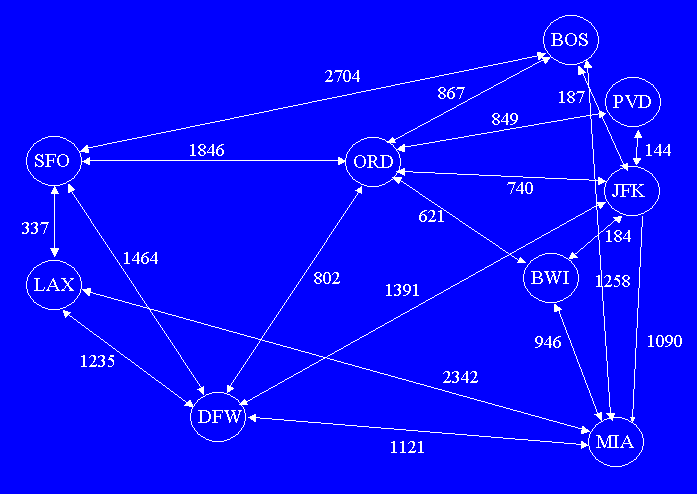
Graphs consist of a collection of nodes (aka vertices), each with a label it is known by. Edges (aka arcs) occur between pair of nodes, and each edge can have an associated value (used to encode a variety of information: often a number, for the length of the edge, the cost of the edge, etc). In a directed graph (aka digraph, the kind we will study), edges have a distinguishable origin and destination node; an edge is written as an arrow from its origin to its destination. A graph might contain just one edge between two nodes, or it might contain two: one from the first to the second, and one back from the second to the first (with each edge associated with its own value). A directed graph is weakly-symmetric if when there is an edge from node1 to node2, then there also is an edge from node2 to node1; likewise, a directed graph is strongly-symmetric if when there is an edge from node1 to node2, then there also is an edge from node2 to node1 with the associated values for these edges equal. In an undirected graph, there can be only one edge between any pair of nodes: each node serves as an origin and a destination. A subgraph of a graph contains a subset of its nodes and edges. The natural subgraph of a graph (containing a certain subset of nodes) includes all the edges in the graph that have a node in this subset as both an origin and destination node. We have used graphs, informally, in the collection class problems. There, we represented a graph by a map whose key is the name of a node and whose value is the set of nodes that it reaches. In this representation of a directed graph, we omitted the value for the edge and the ability to find the nodes leading into a node easily. Both of these deficiencies are removed in the actual graph classes we implement below. A graph with N nodes can have between 0 and N2 edges (in this case, every node has an edge leading to every other node, including itself. We call a graph sparse if it has O(N) edges; likewise we call a graph dense if it has O(N2) edges. The in-degree of a node is a count of the number of edges having this node as their destination; likewise, the out-degree of a node is a count of the number of edges having this node as their origin. The degree of a node is the sum of its in-degree and out-degree. A node is considered a source in a graph if it has in-degree of 0 (no nodes have a source as their destination); likewise, a node is considered a sink in a graph if it has out-degree of 0 (no nodes have a sink as their source). A path is a sequence of nodes a1, a2, ... an, such that there is an edge from ai to ai+1. A graph is cyclic if it has some path that contains the same node twice. Such a path is called a cycle. Likewise, if a graphy contains no cycles, the graph is acyclic (aka noncyclic). A graph is connected if there is a path between any two nodes. If a graph is not connected, it can be decomposed into its connected components: each is the largest subgraph that is connected. Note that is two components both include the same node, then the can be merged into a larger component. For an acyclic graph, each node appears in its own connected component. A spanning tree is an acyclic subset of a graph that represents an N-ary tree; we can choose any node as the root. Typically, there are many spanning trees for a graph. A minimum spanning tree is one that minimizes the sum of the values associated with all the edges contained in the spanning tree. The transitive closure of a graph is a graph with no fewer nodes such that if there is a path from node1 to node2 in the original graph, there is an edge from node1 to node2 in the transitive closure (and its value is often related to the values on the path: one useful way to do this is to assign the value of this edge to be the minimum sum of edge values on any path between the nodes). Below is a directed graph in which the nodes represent airports and the edges represent flights from one airport to another. The edge values represent the mileage for each flight (or, they could represent the cost of an airplane ticket for that flight, the time of the flight, etc). This graph is strongly symmetic; rather than showing to edges connecting each pair of nodes, we show one (double-arrowed) edge.
|
|
This graph is taken from the excellent book: Goodrich and Tamassia,
" Data Structures and Algorithms in Java", John Wiley & Sons, 1998.
Let's state some facts about this tree using some of the terminology defined above.
A similar but much more extensive graph is used as the underlying data structure in Mapquest, a web site that plans travel routes, including computing the amount of travel time. Note that real graphs might model one-way streets (so there may be an edge -a street that one can travel- from corner1 to corner2 but not vice versa). Also, some roads may be partitioned into more lanes going one way than the other, so although there are edges going each way, their values might be different. In the future, programs such a Mapquest might take into account what time you are traveling (in some places, traffic patterns vary tremendously from the norm during rush hours); in fact, if billions of sensors are placed on roads throughout the US, they could report traffic slowdowns to Mapquest, which could contact you in your car (via something like the Onstar system) and automatically reroute you to avoid such delays. Graphs can also easily model the servers (nodes) and transmission lines (edges, with their transmission speeds/capacities -bandwidth- indicated by their values) of the internet. We can ask questions like what is the minimum time it would take to transmit a large number of web pages from one server to another using all the paths available, not exceeding the bandwidth of any transmission line. This problem, a bit beyond the scope of this course, was originally solved by the Ford-Fulkerson algorithm, and improved by the Edmonds-Karp algorithm, whose complexity class is O(nm2), where n is the number of nodes and m is the number of edges respectively in the graph. |
| The Graph Interface |
Graphs are rich data structures.
We will use the following interface to define the methods that we can use to
query and update any graph.
Note that just as the Map interface defines the nested Entry
interface, the Graph interface defines the nested Edge
interface.
Some methods have an Edge as a parameter: many methods return
Sets, where each value in the set is an Edge.
public interface Graph {
//Mutators
public void clear ();
public Graph addNode (String nodeName);
public Graph addEdge (String origin, String destination, Object value);
public Graph addEdge (Edge edge, Object edgeValue);
public Graph removeNode (String nodeName);
public Graph removeEdge (String origin, String destination);
public Graph removeEdge (Edge edge);
public Graph load (TypedBufferReader input , char tokenSeparator);
public void write (TypedBufferWriter output, char tokenSeparator);
//Accessors
public EdgeValueIO getEdgeValueIO ();
public int getNodeCount ();
public int getEdgeCount ();
public boolean hasNode (String nodeName);
public boolean hasEdge (String origin, String destination);
public boolean hasEdge (Edge edge);
public Object getEdgeValue (String origin, String destination);
public Object getEdgeValue (Edge edge);
public int inDegree (String nodeName);
public int outDegree (String nodeName);
public int degree (String nodeName);
//The returned sets are all unmodifiable
public Set getAllNodes ();
public Set getAllEdges ();
public Set getOutNodes (String nodeName);
public Set getInNodes (String nodeName);
public Set getOutEdges (String nodeName);
public Set getInEdges (String nodeName);
//Inner interface
public interface Edge {
public String getOrigin();
public String getDestination();
public Object getValue();
}
}
In addition, we will use objects constructed from classes implementing the
following interface when constructing a graph.
The two methods specified in it are useful in the load and write
methods for graphs: when reading/writing files they help convert edge values
to Strings and vice versa.
public interface EdgeValueIO {
public Object readEdgeValue (String s);
public String writeEdgeValue (Object o);
}
Given these interfaces, we can use it to implement many general algorithms to
process graphs.
One simple one is shown below.
|
| Simple Algorithms |
In this section we will discuss topological sorting as an example of a simple
graph algorithm.
Imagine we model a process by encoding nodes as tasks and edges specifying
which tasks must come before which others: if there is a directed edge from
node 1 to node 2, then the task at node 1 must be completed before the task
at node 1 (we will associate no value with an edge).
For example, we can simply model a cake-making task as follows.
|
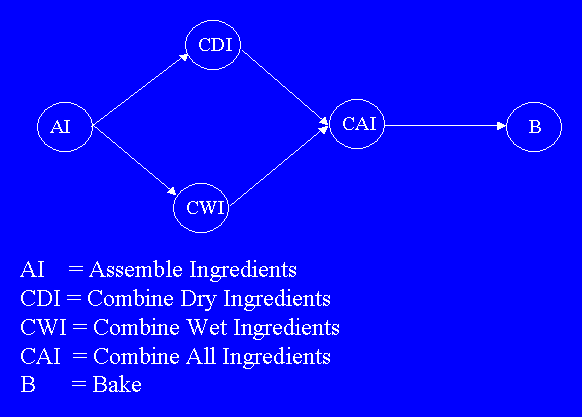
|
Other tasks, like building a skyscraper, can be modeled similarly but with
much more complexity (tens of thousand or hundreds of thousands of subtasks
and ordering relationships).
The problem is to sort all the tasks into a linear sequence, so that if we perform the tasks in that order, all the ordering relationships are observed. All the standard sorting algorithms do not work, because they assume the law of trichotomy: given two values, the first is less than, equal to, or greater than the third. In the example above, the nodes labeled CDI and CWI cannot be compared: either task can be completed before the other. In such cases, we must use topological sorting to solve the problem. Note that this method works only on acyclical graphs: if a graph has a cycle, then we cannot require any node be listed first, because each node has another one the precedes it in the cycle. The algorithm for topological sorting is
We can implement this algorithm as follows Graph g = new HashGraph(new NoEdgeValue());
List l = new ArrayList();
g.load(new TypedBufferReader("Enter file with graph to sort"));
for(;g.getNodeCount()>0;)
for (Iterator nodes=g.getAllNodes().iterator(); nodes.hasNext(); ) {
String n = (String)nodes.next();
if (g.inDegree(n) == 0) { //If node is a source
l.add(n); //Add it next in the list
g.remove(n); //Remove it from graph
break; //Restart iterator
}
if (!nodes.hasNext()) //Iterator about to finish?
throw new IllegalStateException("No source: must be cyclic!");
}
We loop so long as there are nodes in the graph to process; each time.
we iterate over all the nodes.
When we find one with an in-degree of 0, we add it to the list and remove it
(by using the iterator, both from the set of nodes and from the graph
itself, including all its in/out edges).
We then must break, because removing the node will cause the iterator
to throw the ConcurrentModificationException.
Finally, if when iterating over the nodes none has in-degree 0, it means
that the graph must be cyclic.
The complexity class of this algorithm is O(N2), since the outer loop is executed at most N times (at most once to remove each node from the graph) and the inner loop is executed at most N times (at worst removing just one node for each full iteration). A similar problem in the C/C++ programming languages involves compiling a system comprising very many files, with constraints on which files must be compiled first (this is not a problem in Java). Often programmers create "make files" that contain such ordering information, specifying that one file must be compiled before another. We can create a graph, based on the model above, and then topologically sort it, to determine a legal order in which to compile the files. If there are multiple bakers (or multiple computers), we can modify the topological sorting algorithm on the graph to have as many tasks being simultaneously worked on as is allowed by the ordering constraints. |
| Problem Set |
To ensure that you understand all the material in this lecture, please solve
the the announced problems after you read the lecture.
If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a CA, or any other student.
|