| Introduction |
In this lecture, we will take another big step (like our understanding of
Object) towards generalizing our understanding of Java classes,
through the use of interfaces.
This step will ultimately lead to us learning about class inheritance, class
hierarchies, abstract classes (and abstract methods), and other advanced
topics concerning classes.
But, we will start small; we will show how interfaces can be used to
generalize the concept of type: at present we know only that
primitive types and classes can serve as types for local variables,
parameter variables, and fields in classes.
We also know that a variable of the type Object can store a reference
to any object constructed from a class.
An interface specifies a constraint on a class: any class that implements an interface must satisfy its constraints by defining all the methods specified in the interface. To understand all the material in this lecture about interfaces, we must learn how the four facets of interfaces interconnect.
To illustrate all these points concretely, we will first examine two simple but powerful methods (both are public static) whose parameter types are specified by interfaces: one rejects bad values entered by the user in prompts; the other approximates the definite integral of any univariate function. Along with these methods we discuss the necessary interfaces, a few classes that implement these interfaces, and a driver application that ties all these facets together. Please download, unzip, run and examine the entire Interface Demonstration application. Next we will examine the Comparator interface, which is defined in the standard Java library. We will use this interface (whose central method specifies Object parameters) along with the sort method defined in the Arrays class (also in the standard Java library) to learn how to sort any array: in the process, we will use lots of casting. Please download, unzip, run and examine the entire Sorting (with Interfaces) Demonstration application. Each facet of interfaces is simple to undertand by itself: together they provide a powerful programming tool. We will discuss these four facets thrice: once for the prompting method, once for the integration method, and once for the sorting method. Because these facets are so interrelated, it is useful to view everything more than once. Like many advanced Java features, the ability to discuss them technically is critical. Once you can connect up the words, connecting up the concepts (and actually writing the Java code) becomes much simpler. |
| Facet 1: Specifying Interfaces |
An interface specifies a type by specifying the prototypes of what
methods must be defined in any class implementing that interface.
For this reason, interfaces look a lot like class definitions; but, they
cannot specify any constructors and typically do not specify any fields
(fields are allowed, with all sorts of special constraints, so we will
delay studying them).
In fact, each method specification itself is a just a header followed by a
semi-colon (not the body of the header: interfaces specify WHAT methods
must be available but not HOW they are implemented).
Each is like a prototype (but with parameter names).
Interfaces are often very small; the classes implementing them are also as small, or they may define some other methods (as well as constructors and fields) not specified in the interface. So, for example, the DecisionInt interface (shown below and in the Interface Demonstration) is simply specified as public interface DecisionInt {
public boolean isOK(int x);
}
First, notice that the word interface appears before the name
DecisionInt (we have seen class used similarly).
Any class implementing the DecisionInt interface must define a method
named isOK with its prototype; one int parameter returning
a boolean result.
All methods defined in an interface are implicitly public whether or
not they include that access modifier; for this reason, some programmers
never bother to write public, while I always write it for emphasis.
We will see a variety of classes that each implement this interface, with a different meaning for each isOK method (some allowing the user to enter only positive numbers, even numbers, prime numbers, or numbers in a certain range). Then we will see a method that prompts the user for an integer, and calls isOK (on some object constructed from a class that implements this interface) to decide whether the entered value is to be accepted or rejected; if rejected, the user is reprompted to enter an "OK" values. |
| Facet 2: Classes Implementing Interfaces |
Classes implement interfaces by (a) explicitly specifying that they do, and
by (b) implementing whatever methods are required by the interface.
For example, using the isOK interface specified above, we can define
the IsEven class as
public class IsEven implements DecisionInt {
public boolean isOK(int x)
{return x%2 == 0;}
}
Notice the first line in this example: it defines the class name, and then
using the keyword implements specifies an interface that it
implements (more complicated classes can implement multiple interfaces).
Sure enough, this class does supply the required isOK method, having
the correct prototype.
This isOK method just returns true when its parameter is an
even number.
Notice that this class includes no constructor. Recall that in such cases, Java automatically supplies a constructor, written as public IsEven ()
{}
Such a constructor takes no parameters and performs no actions (and obviously
initializes no instance variables: IsEven defines none).
We could have written exactly this code for the constructor inside the class,
but in classes like this one, most programmers let Java supply this
constructor automatically.
Likewise, it is simple to define classes whose isOK methods allows
only positive or prime numbers; their bodies would perform different
computations.
For a more interesting second example, here is another class that implements the DecisionInt interface. public class IsBetween implements DecisionInt {
public IsBetween(int low, int high)
{
if (low > high)
throw new IllegalArgumentException
("IsBetween Constructor: low("+low+") not <= high("+high+")");
this.low = low;
this.high = high;
}
public boolean isOK(int x)
{return low <= x && x <= high;}
private int low;
private int high;
}
This class specifies two instance variables, and a constructor that checks
for legal values (low must be no bigger than high) before
storing its parameters into these instance
variables.
Instead of throwing an exception when the parameters are out of order, we
could just fix them, and write this constructor as
public IsBetween (int bound1, int bound2)
{
low = Math.min(bound1,bound2);
high = Math.max(bound1,bound2);
}
But, I'm not a big fan to automatically fixing such problems: better to
throw an exception and let someone know about the problem.
In either case, once an object is constructed and correctly stores these two values, the isOK method determines whether its supplied parameter is between them. Of course, this class correctly implements the DecisionInt interface with its isOK method. What makes this class more interesting than IsEven is that it must store instance variables, and therefore uses a constructor to initialize them correctly. The isOK method in InBetween compares its single parameter to these instance variables; its prototype looks just like all the other isOK methods (it just is more complex on the inside). Note that if a class specifies that it implements some interface, the Java compiler checks whether all the methods specified in the interface are actually defined in the class (with their correct prototypes). If not, the Java compiler detects and reports an error. Finally, one class can implement many different interfaces (just as one method can throw many different exceptions), as long as it defines all the methods specified in each interface that it claims to implement. We will see this more advanced feature used later in the course. |
| Facet 3: Interfaces as Types in Methods |
Interaces are types.
We can use the names of interfaces to declare variables: local and parameter
variables in methods, and instance variables in classes.
This simple statement leads to some extremely interesting and deep ideas in
object-oriented programming.
What can we do with a variable whose type is declared by the name of an
interface?
|
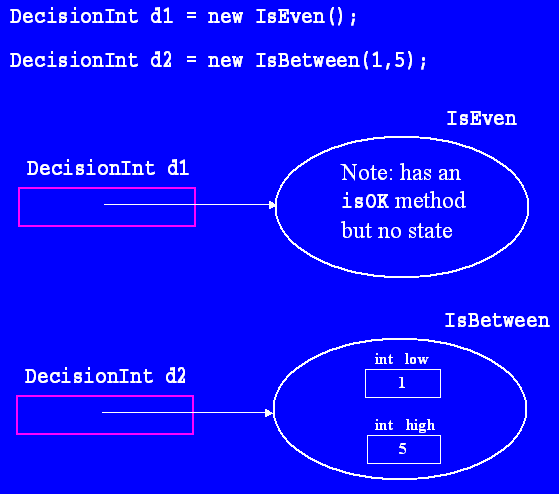
|
This picture illustrates a situation that we have seen only once before, when dealing with the type Object: the type of the variable is COMPATIBLE, but NOT IDENTICAL to the type of the constructed object to which it refers! But unlike the Object type, which can store ANY reference, a variable using an interface type can store REFERENCES ONLY TO OBJECTS CONSTRUCTED FROM A CLASS THAT IMPLEMENTS THAT INTERFACE. Because the IsEven and IsBetween classes each implement the DecisionInt interface, we can make variables declared from the DecisionInt interface/type refer to objects constructed from either of these classes. Once we have variables like d1 and d2, which refer to objects constructed from classes implementing an interface, we can use them to call any method specified in the interface. So, in these case, we can use each to call only a method named isOK. Which isOK method is called depends entirely on the class of object that the variable refers to. Given the above variable declarations, calling d1.isOK(3) would return false; it calls the isOK method declared in IsEven, the class of the object that d1 refers to. Likewise calling d2.isOK(3) would return true; it calls the isOK method declared in IsBetween, the class of the object that d2 refers to -and this object stores 1 and 5 for its bounds. Generally, a variable specifying an interface type knows WHAT method names it can call (those specified in the interface) but not HOW these methods will compute their result (that depends on what object was constructed to store in such a variable. This rule is very echoes what we know about the Object type too.
Now, let's examine another useful prompting method; one that has a DecisionInt parameter. We will define this forInt method in a class named AdvancedPrompt. It actually specifies three parameters: a message to prompt the user, a reference to an object constructed from some class that implements the DecisionType interface, and another message -an "error" message. public class AdvancedPrompt {
public static int forInt (String message,
DecisionInt check,
String errorMessage)
{
for(;;) {
int answer = Prompt.forInt(message);
if (check.isOK(answer))
return answer;
System.out.println(errorMessage);
}
}
}
This method first prompts the user for an int value using the standard
Prompt.forInt method, storing its result in answer (all
possible problems with the user entering non-integer values are handled by
Prompt.forInt).
It then uses answer as a parameter to the isOK method of the
object to which check refers; if the isOK method called
returns true, then this method returns answer; if not, then
this method prints an error message and repeats the prompt-check loop.
Notice that the only use of the check parameter inside the method is a call to its isOK method. Because we know that check refers to an object from some class implementing the DecisionInt interface (the compiler doesn't allow any arguments not constructed from such a class), we know that the object it refers to will contain an isOK method. So, we have written a very general method. It accepts/rejects the information entered by users; its action depends on whatever object is passed as an argument to the check parameter. There might be hundreds of different criteria we want to use for different prompts, but we can alway use this method, along with a class that implements the criteria we want. |
| Facet 4: Calling Methods with Interface Parameters |
We can now complete the example, by showing how to call the
AdvancedPrompt.forInt method.
Given the declarations above, we can write
int even = AdvancedPrompt.forInt("Enter even",
d1,
"...not divisible by two");
which could have the following interaction in the console:
Enter even: 3 ...not divisible by two Enter even: 4at which point the value 4 is stored into the variable even. Likewise, we can use d2 instead of d1 and write int selection = AdvancedPrompt.forInt("Enter selection",
d2,
"...not in range [1..5]");
which could have the following interaction in the console:
Enter selection: 7 ...not in range [1..5] Enter selection: 4at which point the value 4 is stored into the variable selection. In fact, we do not even need to store an object in a variable before calling AdvancedPrompt.forInt! We could directly write int selection = AdvancedPrompt.forInt("Enter selection",
new IsBetween(1,5),
"...not in range [1..5]");
Here, the second argument is an expression that evaluates to a reference to
an object constructed from the class IsBetween; its value is copied
into the check parameter in the method.
Here is a call frame illustrating everything (assuming the user enter 4, the
method returns 4).
|
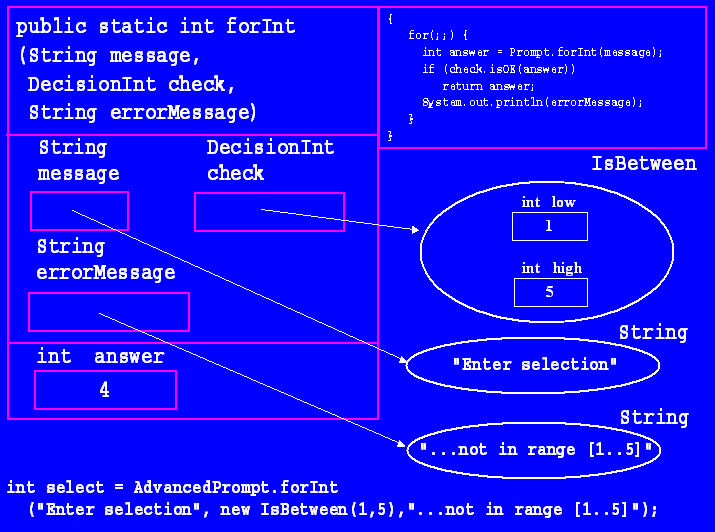
|
What have we accomplished with these four facets of interfaces? Primarily, we have separated the AdvancePrompt.forInt method from the method(s) that determines whether to accept/reject the value entered by the user (the isOK method, in whatever object we pass to this method, controls the semantics of choosing). In the process, we have also specified the DecisionInt interface, as what interconnects these methods. If we want a new way to filter prompts, all we must do is plug an object from a new class into machinery that we have created: write a class that implements the DecisionInt interface, and construct an instance of that class to pass as a parameter to AdvancedPrompt.forInt. Thus, this mechanism provides a general structure for solving yet-unspeciried problems of differentiating good or bad input values. |
| All Four Facets: Integration |
Let's solve another completely different and general problem using
interfaces.
Suppose that we want to be able to write a method that allows us to
approximate the area under a curve.
We can do this by repeated summing the areas of small rectangles under the
curve.
Each rectangle's height corresponds to a value of the function F(...);
each rectangle's width is the constant h.
So, to compute the area under the curve from a to b, we compute
F(a)h + F(a+2h)h + F(a+3h)h + ... F(b-h)h, as illustrated in the
following picture.
(This is not the best way to approximate this area, but it is the simplest.)
|
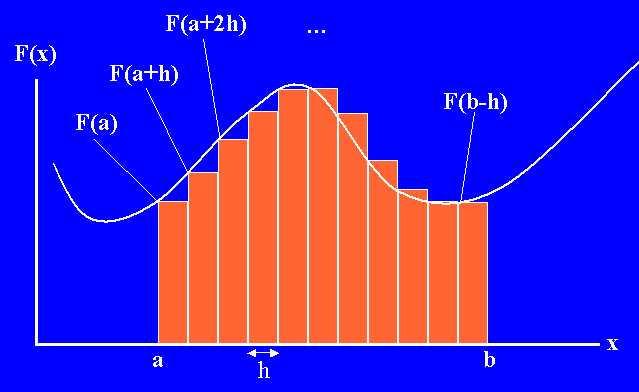
Let's examine the four facets of interfaces to solve this problem.
First, we must specify the interface, which supplies a method to compute the
value of a function of one variable: a univariate function.
We don't know how this will be done (just as we didn't know how a method
would compute whether to accept/reject a value), but we know what the
prototype of the method must be.
So we can write this interface simply (as simply as DecisionInt)
public interface Univariate {
public double evaluate (double x);
}
Second, we must write a class that implements this interface. As an example, let's write a class that can easily represent all quadratic forms: ax2+bx+c. public class Quadratic implements Univariate {
public Quadratic (double a, double b, double c)
{
this.a = a;
this.b = b;
this.c = c;
}
public double evaluate (double x)
{return a*x*x + b*x + c;}
private double a,b,c;
}
Third, we must write a method that approximates the integral for an
arbitrary univariate function.
We will call such a method integrate and define it in the
AdvancedMath class as follows
public class AdvancedMath {
public static double integrate (Univariate f,
double low, double high,
double step)
{
double sum = 0.;
for(double x = low; x < high; x+=step)
sum += f.evaluate(x) * step;
return sum;
}
}
Note that we use the parameter f just once in this code, calling its
evaluate method for all the different values of x generated
by the for loop (so it does get called many times when the method
executes: once for each rectangle).
Note too that this for loop uses double values: a legal, but
not frequent choice.
Finally, let's combine all this information to write a call that approximates the area under the curve 2x2-3x+5 between 1 and 3.5 using a step-width/h of .01. We can do this in one line. double area = AdvancedMath.integrate(new Quadratic(2.,-3.,5.), 1., 3.5, .01); We can also define many other methods in the AdvancedMath class that operate on univariate functions: finding 0s, computing maxima/minima, approximating derivatives, etc. We can also define many other classes that implement the Univariate interface: cubics, exponentials, trigononmetric functions, and combinations of all these. Then, we can mix and match these as necessary: say, use the findZero method on an object constructed from the Cubic class. The more we build these libraries, the more likely we are to find debugged classes that we can use directly from them in our new applications. |
| The Comparator Interface and the sort method in Arrays |
The standard Java library contains an interface named Comparator,
defined in the java.util package.
Find the Javadoc for this interface and scan its documentation.
Notice that in the All Classes pane -interfaces appear here
too- its name appears italicized as Comparator.
In fact, the names of all interfaces appear here italicized, so you can
quickly tell whether an identifier names a class or an interface (these
are the only two possibilities).
The Comparator interface is defined by
public interface Comparator {
public int compare (Object o1, Object o2);
public boolean equals (Object obj);
}
Of these two methods, compare is the most important by far.
Primarily, classes implementing this interface use compare to
perform a trichotomous comparison of two arguments: telling whether the
first parameter is (a) less than (returning any negative number) the
second parameter, (b) equal to (returning 0) the second parameter,
or (c) greater than (returning any posive numbers) the second parameter.
Interfaces are general to being with, allowing lots of different class to implement them. In addition, this interface uses the type Object for parameters in the compare methods. This is a tipoff that this interface is very general and very useful! Let's first write a class implementing the Comparator interface for objects constructed from the Integer wrapper class. Then we will see how to use objects constructed from this class in a sorting method in the standard Java library. public class IntegerComparator implements Comparator {
public int compare (Object o1, Object o2)
{
Integer i1 = (Integer)o1;
Integer i2 = (Integer)o2;
return i1.compareTo(i2);
}
public boolean equals(Object obj)
{return (obj instanceof IntegerComparator);}
}
Notice that the compare method first casts both parameters
and stores their references into Integer local variables; if
either cast fails, Java will automatically throw
a ClassCastException.
Then it calls the compareTo method on the first Integer, using
the second as an argument.
This method conveniently is defined in the Integer wrapper class
(look it up) to compute the trichotomous result easily: it returns exactly
the value that we want compare to return!
In fact, because the non-static compareTo method has the
prototype int compareTo(Object) we could simplify the body of
compare to just return ((Integer)o1).compareTo(i2); because
compareTo will by itself cast its argument to be an Integer.
(Why can't we write just return o1.compareTo(o2);?)
The equals method just returns whether obj is also an instance of this IntegerComparator class; any two instance of this class have the same state, because the class stores no instance variables that can be different! Thus any two IntegerComparator objects will return the same results when their compare methods are called.
Finally, Java will write automatically write the constructor
So, if Java executed the code
How hard would it be to sort the array in the other direction:
from biggest to smallest.
We could just replace the call
public class ReverseIntegerComparator implements Comparator {
public int compare (Object o1, Object o2)
{
Integer i1 = (Integer)o1;
Integer i2 = (Integer)o2;
return -i1.compareTo(i2); //Notice negation!
}
public boolean equals(Object obj)
{return (obj instanceof ReverseIntegerComparator);}
}
By negating the original returned result
In fact, we can write a class with the following amazing property:
its constructor will take any Comparator and produce an
object that is also a Comparator, but one that returns the
opposite result..
With this class in our library (ReverseAComparator is in fact in the
course library), we can instead of the above write
public class ReverseAComparator implements Comparator {
public ReverseAComparator(Comparator c)
{realComparator = c;}
public int compare (Object o1, Object o2)
{return -realComparator.compare(o1,o2);}
public boolean equals(Object obj)
{
return (obj instanceof ReverseAComparator) &&
realComparator.equals(
((ReverseAComparator)obj).realComparator);
}
private final Comparator realComparator;
}
This class uses a decorator pattern: it produces an object
on which we can call the same methods as the object that it was
constructed with: it decorates the original object.
I vastly prefer to write and debug a general class and use it multiple
times than write multiple classes.
Decorators capture exactly this desire.
Notice what equals checks: obj is an instance of ReverseAComparator, and that both realComparators are equals. Here there is state in the class, so we need to check it for equality. As a final example of a class that implements Comparator, imagine that we have declared DiceEnsemble[] ds; and stored into it a reference to an array object filled with references to DiceEnsemble) objects. Now, suppose that we wanted to sort these ensembles, so that the fewer times they were rolled, the early they appear in the sorted array. Here is the class needed by Arrays.sort: public class RolledComparator implements Comparator {
public int compare (Object o1, Object o2)
{
DiceEnsemble d1 = (DiceEnsemble)o1;
DiceEnsemble d2 = (DiceEnsemble)o2;
return d1.getRollCount() - d2.getRollCount();
}
public boolean equals(Object obj)
{return (obj instanceof RolledComparator);}
}
Notice how simple this class is to write; it looks just like the
other classes we wrote implementing the Comparator interface.
Thus, we should consider it simple to use Arrays.sort to sort
any array, using any ordering criteria; all we need to do is to write a
simple class implementing the Comparator interface that establishes
the ordering, and call Arrays.sort with it and the array to sort.
So, it would also be simple to sort a DiceEnsemble[], either in
increasing or decreasing order, the number of times each ensemble was
rolled, by the number of dice in each ensemble, by the sum of the pips
showing in each ensemble, etc.
|
| Loose Ends |
In this section we will discuss a few loose ends about interfaces.
First, what happens if a class does not specify that it implements an
interface (doesn't use that keyword in its definition) but actually
defines all the methods that the interface specifies?
Can we construct an object from this class and store it in a variable whose
type is the interface?
The answer is no.
More concretely, if we define (notice, no implements DecisionInt) public class IsPositive {
public boolean isOK(int x)
{return x > 0;}
}
then we CANNOT write
int answer = AdvancedPrompt.forInt("Enter Positive",
new IsPositive(),
"...bad choice");
The Java compiler believes that an object constructed from the class
IsPositive cannot be passed to a parameter whose type is specified
by DecisionInt.
So, when it comes to interfaces, it does not matter whether or not a class
implements the specifications in an interface: it does matter whether or
not its definitions says that it implements the interface.
Of course, if it says it does, but really doesn't, the Java compiler will
detect and report an error when it tries to compile that class.
Second, what happens if we have a variable whose type is specified by an interface, and we try to use it to call a method that is not specified in the interface. Whether or not the object that it refers to has such a method, the Java compiler will detect and report an error. The only methods that the Java compiler allows to be called on a variable whose type is an interface, are those methods specified in the interface. Again, this is very important for our future study of Java. Third, even if we leave off public when specifying an interface, it is declared public by default (the same holds for all its method specifications). The whole purpose of an interface is to specify methods that a class must define, that we can call: so they can be only public. Fourth, can we construct an object from an interface? Again, the answer is no. If we tried, the Java compiler would detect and report an error. So, writing DecisionInt d = new DecisionInt(); is MEANINGLESS to Java and NOT ALLOWED. Thus, the declare/constuct pattern that we've seen does not work for interfaces (but see below for how we can use an interface to construct an object from an anonymous class)! Finally, in reality interfaces can also specify public static fields. Although doing so it legal, it is not often done. In fact, even if the fields are not specified with these access modifiers, they are automatically applied by Java. One more generalization. We can use the names of interfaces in instanceof and class casting. If x is the name of a reference variable and I is the name of an interface, Java's returns true for x instanceof I if x refers to an object constructed from any class that implements I. If we cast (I)x, Java treats the resulting reference as if it refers to an object constructed from any class that implements I; thus, we can call any methods specified in I on the casted reference, or store it in a variable whose type is specified by I. |
| Anonymous Classes |
Sometimes we want to construct just one object from a class that
implements an interface; and often, that class is very small: it
defines few members because interfaces are often small.
If that class has no constructor too, Java allows us to construct an object
from it anonymously, by using the name of the interface directly.
Before we get to the main example of an anonymous class, we need to deal with one more point. When we study inheritance, we will learn that every class automatically inherits an equals method; if we never call this method, there is no reason for another class to override it. When calling Arrays.sort with any class implementing the Comparator interface, the equals method is never called, so we can inherit its (incorrect) definition and not bother redefinining it, and sorting still works. Thus, we really have to define only the compare method.
Now, Java allows us to construct an object from an anonymous class by
directly using an interface.
For example, we can call
|
| Problem Set |
To ensure that you understand all the material in this lecture, please solve
the the announced problems after you read the lecture.
If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a CA, or any other student.
|