Variables, Operators, and Expressions

Finally, we will learn how to combine literals, variables, operators, and methods (which are like function calls) to build arbitrarily complicated expresions (formulas that Java can evaluate). We being by examining the structure and evaluation process for expressions, including the concepts of operator precedence and operator associativity. Then we will learn how to build oval diagrams: the main analytic tool that we will use to investigate/understand large expressions (along with our knowledge of prototypes). We should understand how to translate complicated formulas into their equivalent Java expressions and verify the translation is correct.

The EBNF rules for variable declaration appear below. Each declaration is a statement -a complete command to the computer- which the computer executes. We will cover many of Java's other statements in the next lecture.

    primitive-type  <= int | double | boolean | char
    reference-type <= String | ... (we will learn others soon)
    type                 <= primitive-type | reference-type

    expression <= literal | ... (we will generalize this rule later)

    variable-declarator  <= identifier [=expression]
    variable-declarators <= variable-declarator{,variable-declarator}

    local-variable-declaration-statement <= type variable-declarators ;

Declarations are simple statements, which means that they end with a semicolon (see the last rule above). Variables are always declared with a type (e.g., a primitive type like int or a reference type like String), one or more names (an identifier that the programmmer chooses) whic can be optionally initialized to store a specified value.

The simplest form of a declaration is int sum; which declares a variable named sum to be of the type int, meaning that sum stores only int values. Again, notice the semicolon ending this statement. When a variable is declared this way, the value that it initially stores is undefined. We will have more to say about what Java does with undefined variables later; it is not a mistake to declare certain variables without initializing them.

If we want to declare a variable and at the same time initialize it, we can write something like int gamesPlayed = 0; explicitly telling Java to store zero in this variable initially.

In fact, we can declare a few variables in the same declaration: e.g., double angle, magnitude; declares two variables, both of type double and both storing unknown values. In multi-variable declarations, all the variables are declared to be of the same type -the one type that starts the declaration.

If we want to declare and initialize multiple variables in a single declaration (using the repetition in the variable-declarators EBNF rule), we must explicity specify the initial value of each variable. For example, int n = 0, sum = 0; initializes each variable to zero. WARNING: int n,sum = 0; initializes sum to zero, but leaves n uninitialized; making this mistake is common for beginning programmers. In fact, Java always executes declarations with multiple variables as a sequence of declarations of single variables. So executing int n,sum = 0; is equivalent to executing int n; then int sum = 0;, which makes this problem obvious.

Java imposes a syntax constraint on initialized variables: the type of the variable must be compatible with the type of the expression. We will discuss compatibility more, when we discuss implicit conversions; for now, assume that the two type must be the same.

So in the declaration int n = true; although the syntax is correct, the Java compiler will detect and report a syntax constraint error because true (a boolean literal) is not an int value; likewise boolean atCapacity = 0; exhibits the same error.

To be truthful, Java will in fact automatically convert an int value into a double if necessary , so double x = 1; is legal, and is treated as equivalently to double x = 1.; More obscurely, Java will automatically convert a char value into an int value (and vice-versa) if necessary. We will learn more about implicit type conversion later in this lecture.

Programmers often use line-oriented comments (here called side-bar comments) in declarations to document some interesting facet of a variable that is not captured by even a well-chosen name. For example, in the declarations statements

    double  tankSize;        //Gallons
    double  mileage;         //Miles/Gallon

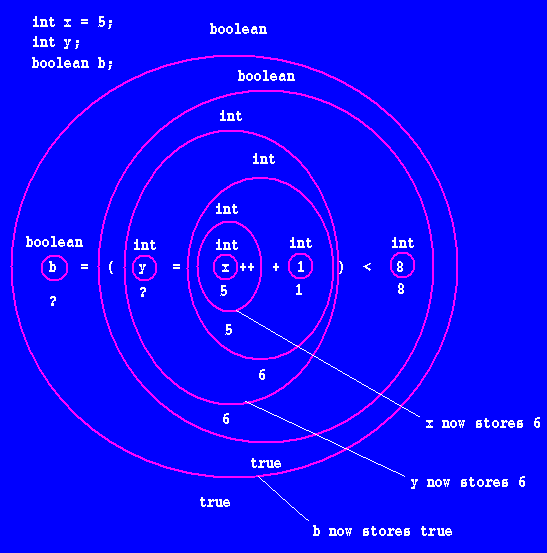
To illustrate the meaning of a declaration, we draw a box: we label the box on the top left with the variable's type and on the top right with the variable's name; we store the initial value (if any) inside the box; if the declarator specifies no initialization option, we write a question mark inside the box. So, we always write something in each box: a value of the right type or a question mark (not a char or String literal: just a question mark).

Ther are two major categories of types in Java: primitive and reference. All primitive types are fixed in the language, named by keywords; we will learn more about, and repeatedly use the primitive types int, double, boolean, and char. All reference types come from class libraries that are written by programmers Right now, the only reference type that we currently know is String, which is declared in the standard Java library. We will learn about other reference types soon, and how to declare our own new reference types a bit later. The String reference type is special, because it is the only one that also has literal values..

The only difference between primitive and reference types is what can appear inside the box in the picture of a variable. Variables declared of a primitive type store values; variables declared of a reference type store references. For a variable of a primitive type, we write in its box either a question mark or a literal of the declared type. For a variable of a reference type, we write in its box either a question mark, the literal value null (usable for all reference types: it means that the variable refers to nothing), or an arrow (called a reference) that leads to an object (an oval labelled by the same type) that stores a collection of data (for Strings, the collection of characters that comprise the String's value).

We will learn much much more about primitive and reference types later. For now, it is critical just that you understand, given a declaration, how to illustrate its meaning with a picture. The pictures below illustate the meaning of the following declarations.

    int     a;
    int     b = 0;
    boolean c = false;
    String  d;
    String  e = null;
    String  f = "Hello";
  

We will explore such illustrations further when we learn about state-change operators. We will extend such illustration when we learn about methods (which declare parameter variables) and objects (whose classes declare instance variables).

1. Describe their syntax via prototypes
   • what type of operand(s) they work on
   • what type of result they produce
   • whether they can throw any exceptions
2. Describe their semantics/meaning in English
   • how they compute the value of the result from the operand(s)
   • under what conditions they throw an exception

return-type              <= type
operand-types         <= type{,type}
exception-identifier <= ArithmeticException | ... (we will learn more more later)
exception-types       <= exception-identifier{,exception-identifier}

prototype <= return-type operator ([operand-types]) [throws exception-types]

So, prototypes start with the type of the result returned by the operator, followed by the operator itself, followed by a pair of parentheses (with the type(s) of the operand(s), if any, separated by commas, on the inside). For example, each of the following lines specifies an operator prototype:

      int     + (int,int)
      double  - (double)
      int     * (int,int)
      double  * (double,double)

Of course, we already know the semantics/meanings of addition, negation, and multiplication in mathematics, so we do not need to discuss them here. We will soon see prototypes for more interesting operators, such as

      boolean <  (int,int)
      boolean && (boolean,boolean)

As we learn these and more operators in Java, we will first present their syntax (with prototypes) and then their semantics (using English and other tools).

Finally, some operators specify that they throw exceptions. An operator throws an exception if it cannot correctly compute a result for its operand(s). For example, integer division (the / operator in Java) cannot compute a result if its denominator is zero. A prototype indicates this information by using the keyword throws followed by the identifier ArithmeticException (about which we will learn many more details later). So the prototype for integer division is fully written as

      int / (int,int) throws ArithmeticException

A signature is a subset of the information in a prototype; it includes just the information about the types of operands (not the return type and not the exceptions). We can specify the syntax of a signature formally (reusing some of the EBNF rules written above) as

signature <= operator ([operand-types])

• Number of Prototypes
  • An operator is overloaded if it has more than one prototype: e.g, the * operator above has one prototype for int operands and one for double operands, hence it is overloaded.
  • The term overloaded is not a "bad" term; in fact, most Java operators are overloaded.
  • Overloaded operators must have different signatures: i.e., either a different number of operands or the same number but with different types for some operands.
  • Given this restriction, Java can use the types of the operands to determine which prototype to use.
  • Note that we cannot have the following two prototypes for the /
        int        / (int,int)
        double / (int,int)
    because they both have the same signature: / (int,int)
• Number of Operands
  • Unary operators have one operand (e.g., the negate operator; think of a unicycle, with one wheel).
  • Binary operators have two operands (e.g., the multiply operator; think of a bicycle, with two wheels).
• Operator Location
  • Infix operators are written in-between their operands (e.g., 3*5; infix operators are binary).
  • Prefix operators are written before their operand (e.g., -5; prefix operators are unary).
  • Postfix operators are written after their operand (e.g., Count++; postfix perators are unary)

    Arithmetic          +  -  *  /  %
    Relational          ==  !=  <  >  <=  >=
    Logical             !  &&  ||
    State Change        ++  --  =  +=  -=  /=  %=  ...
    Textual             +

    int    + (int)
    double + (double)
    int    + (int,int)
    double + (double,double)

Prototype	Semantics	Examples
int + (int)	A unary prefix operator; its result is the same as its operand.	+7 evaluates to 7
double + (double)	A unary prefix operator; its result is the same as its operand.	+7.25 evaluates to 7.25
int + (int,int)	A binary infix operator; its result is the sum of its operands.	3+5 evaluates to 8
double + (double,double)	A binary infix operator; its result is the sum of its operands.	2.4+5.1 evaluates to 7.5

The + operator is also a textual operator (called catenate), with the following further prototypes (so it is highly overloaded). Notice that in each case at least one operand is a String and the final result is always a String too.

    String + (String,int)
    String + (String,double)
    String + (String,boolean)
    String + (String,char)
    String + (String,String)
    String + (int,String)
    String + (double,String)
    String + (boolean,String)
    String + (char,String)

Note that 1+1 results in 2 while "1"+1 and 1+"1" both result in "11".

Finally, note that true+" is a boolean" results in "true is a boolean" because the boolean value true is first automatically converted into the String value "true".

Using + for catenation is very common in Java, when outputing various types of information to the console. You will become very familiar with this operator soon.

    int    - (int)
    double - (double)
    int    - (int,int)
    double - (double,double)

Prototype	Semantics	Examples
int - (int)	A unary prefix operator; its result is the negated value of its operand.	-7 evaluates to negative 7
double - (double)	A unary prefix operator; its result is the negated value of its operand.	-7.25 evaluates to negative 7.25
int - (int,int)	A binary infix operator; its result is the difference between its first and second operands.	8-3 evaluates to 5
double - (double,double)	A binary infix operator; its result is the difference between it first and second operands.	7.5-2.4 evaluates to 5.1

Note that in Java, writing -6 means negate the literal 6. Recall that all literals are non-negative, so -6 technically is not a literal: it is an operator and a literal; still, we will write -6 and often pretend it is a value. Seem confusing? Don't worry about this detail too much: don't let this weird tree stop you from seeing the forest.

    int    * (int,int)
    double * (double,double)

Prototype	Semantics	Examples
int * (int,int)	A binary infix operator; its result is the product of its operands.	3*5 evaluates to 15
double * (double,double)	A binary infix operator; its result is the product of its operands.	4.2*5.8 evaluates to 24.36

Note that unlike mathematics, there is no "implicit" multiplication in Java. Assuming that we declare int A,B; then 3A and 3(A+B) are NOT LEGAL expressions: they would have to be written explicitly with the * operator as 3*A and 3*(A+B). We will study expressions (with arbitrarily complicated combinations of the operators that we are discussing here) later in this lecture.

    int    / (int,int)       throws ArithmeticException
    double / (double,double)

Prototype	Semantics	Examples
int / (int,int)	A binary infix operator; its result is (the integer part of) the first operand divided by the second (ignore the remainder). If the second operand is 0, this operator throws an exception.	13/5 evaluates to 2
double / (double,double)	A binary infix operator; its result is the first operand divided by the second. If the second operand is 0., this operator returns the result Infinity (if the first operand is positive), or -Infinity (if the first operand is negative), or NaN (Not a Number, if the first operand is also zero).	13./5. evaluates to 2.6

Here are the first "nonintuitive" semantics for a Java arithmetic operator. When Java divides two int values (13 by 5) the prototype tells us that the result must be an int. So, Java takes the "mathematical" answer (the one that is intuitive to us) and truncates it (throws away the non-integral part). Only when two double values are divided does Java keep the decimal part in the returned result. Students find this difference strange and nonintuitive; they often aren't careful, when using the / operator in their programs, to distinguish between int and double operands.

Finally, if the second operand to the / operator (with int operands) is zero, the operator does not compute a result, but instead throws an exception. Throwing an exception is like throwing up your hands and saying, "I cannot do the computation". At the end of our study of Java statements, we will learn how catch (handle) thrown exceptions, so throwing an exception doesn't mean that the program will stop.

The case for the result of the division of two double values is stranger. There is a long and tortured history of how computers should deal with this, and related, problems involving anomalous operations on double values, which was finally resolved in the IEEE 754 standard. We will ignore this issue now, and the problem shouldn't come up in simple programs; but remember that if you print a double and it appears as Infinity, -Infinity or NaN it means you divided by zero.

    int % (int,int) throws ArithmeticException
    double % (double,double)

Prototype	Semantics	Examples
int % (int,int)	A binary infix operator; its result is the remainder left when the first operand is divided by the second. Technically, the result's sign is the same sign of its first operand; the result's magnitude is the same as the remainder when the absolute values of its operands are divided. If the second operand is 0, this operator throws the ArithmeticException.	13%5 evaluates to 3, because 5 goes into 13 just 2 times (13/5 evaluates to 2) leaving a remainder of 3; -13%5 evaluates to -3 because the sign of its first operand is negative and its magnitude is the same as 13%5; 13%-5 evaluates to 3 because the sign of its first operand is positive and its magnitude is the same as 13%5; -13%-5 evaluates to -3 because the sign of its first operand is negative and its magnitude is the same as 13%5
double % (double,double)	This space intentionally left blank.	This space intentionally left blank.

Although most students have never seen this operator in mathematics (but have seen remainders in long division), it is sometimes useful in Java programming (and certainly not that hard to understand, at least in the case of non-negative integers). Therefore, you must know its prototype and semantics for non-negative integers.

Obviously the / and % operators (with int operands) are related: we can call / the quotient operator and % the remainder operator. Generally: x%y, when both are non-negative integers, returns the same value as x-(x/y)*y.

Two interesting facts are that if we declare x to be an int and store a non-negative value in it, x%10 is the last digit of that number and x/10 is every digit but the last one. For example, if we declare int x = 4125; then x%10 evaluates to 5 and x/10 evaluates to 412. You must be able to understand and use both "division" operators in your program.

Finally, as with the / operator, the % operator throws the ArithmeticException if its second operand is zero.

Note the == computes "is equal to" and != computes "is not equal to"; < computes "is less than"; <= computes "is less than or equal to"; > computes "is greather than"; >= computes "is greater than or equal to".

    boolean == (int,int)
    boolean == (double,double)
    boolean == (boolean,boolean)
    boolean == (char,char)

Semantically, these operators work as we would expect on numeric (int and double) values.

Again, one can compare boolean values with == and != but not the other four relational operators.

For the text type char, the values compare according to their ASCII values: each char value can convert to/from a small int according to the ASCII conversion table. You should certainly NOT memorize the ASCII table, but programmers should know that '0'<'1'<...<'9' < 'A'<'B'<...<'Z' < 'a'<'b'<...<'z' in ASCII.

These operators do NOT work in a straightforward way for variables/values of the type String, which you should recall is a class type and not a primitive type. We will discuss later various methods for comparing String values.

    boolean !  (boolean)
    boolean && (boolean, boolean)
    boolean || (boolean, boolean)

A	B	A && B	A || B	!B
false	false	false	false	true
false	true	false	true	false
true	false	false	true
true	true	true	true

Programmers must memorize these tables to be able to analyze expressions that use these operators. Here are some short-cuts. Note that the result of the && operator is true only when both of its operands are true. Note that the result of the || operator is false only when both of its operands are false. Note that the ! operator just has one operand, so it looks a bit different in the truth table.

Java could just rejectusing this combination of operator and operands. Instead, when Java sees a binary operator with one int operand and one double operand, it automatically converts the int value into a double and then uses the double-operands prototype of +(and its related circuit) to do the addition. This is called implicit conversion. Java does implicit conversion (always int to double) whenever a binary arithmetic operator has different numeric types for its operands.

Java performs one other implicit conversion when necessary: a char is implicitly converted to an int (according to its value in the ASCII table). So in 'A'+1, the char 'A' is first implicitly converted to the int 65 so that it can be added to the int 1 finally producing an int result of 66. In fact, in the expression 1.5+'A', 'A' is first implicitly converted to the int 65 and then implicitly converted to the double 65. finally producing an double 66.5 as a result.

Finally, the expression '5'-'0' implicitly converts both char values to int (53 and 48 respectively: see the ASCII table) and then performs subtraction: the result in this case is the int 5. In fact, if we declare char d = '8'; (or any other character that is a digit), then writing d-'0' results in an int equivalent to the digit (in this case 8). Note that the ASCII value of '8' is 56 and of '0' is 48.

Collectively, these implicit conversion are called promotion, which always works in just one way: char promoted to int promoted to double. No promotion loses information: every char can be represented as an equivalent int and every int can be represented as a equivalent double. Notice that the remaining primitive type, boolean, plays no part in promotion.

The most common state-change operator in Java is the = operator. The = operator (known as the assignment or stores operator) is overloaded for each of the primitive types that we know in Java, with the following prototypes.

   int     = (int    , int)
   double  = (double , double)
   boolean = (boolean, boolean)
   char    = (char   , char)  

Semantically, the value of the right operand (which can be any expression) is stored into the variable specified by the left operand (which is restricted to be a variable name), and this value is also the result of the expression. So, we can use state-change operators to change the state (value) stored in any variable.

For example, if we declare int x = 0; and then evaluate the expression x = x+1 Java first computes x+1 (we will soon learn that = has is lower precedence than +, so the + operator is evaluated first) whose result is 1, then Java uses the = operator, which changes the value stored in x to 1; the result (of the entire expression) is 1 also.

Unlike mathematics, writing x=y has a very different meaning than writing y=x. The first expression changes the variable x to store the current value in the variable y; the second changes the variable y to store the current value in the variable x. Again, only the value stored in the first operand (which must be a variable) changes.

If necessary, Java uses implicit conversion with this operator too, converting the type of the right operand before storing its value in the left operand. For example, if we have declared double x; then writing x = 5 stores into x the value 5. (recall that implicit conversion -aka promotion- from int to double is allowed). Note that the Java compiler will not allow int x; then writing x = 5.4 because it will not implicitly convert a double to an int (doing so implicitly would lose all the information after the decimal point).

Java includes a grab-bag of other (two character) state-change operator:
    +=   -=   *=   /=   %=
whose prototypes are all similar: the prototypes for += appears below.

    int    += (int,int)
    double += (double,double)
    char   += (char,char)

Semantically, the expression x+=e is a simpler way to write x = x+(e) (and similarly for the operators -=   *=   /=   and %= ). So x+=2 computes x+2 and then stores the result into x; this new result is also the resuklt of the entire expression: it is equivalent to x=x+2.

Finally, Java includes two very special operators ++ and -- (which increment and decrement variables by 1). Both operators can be used in a prefix or postfix form; they are overloaded for the following types ( and the are restricted to operate on variables names only (we cannot write 1++).

    int    ++ (int)               int    -- (int)
    double ++ (double)            double -- (double)
    char   ++ (char)              char   -- (char)

If the variable is of type char it is changed to store the character one higher (for ++) and one lower (for --).

So, if we declare int x=0, y; and then write y = x++ then x is incremented from 0 to 1, but its result produced by this operator is 0 (the old/original value stored in x), which is stored into y, and this value (0) is the result of the entire expression. If we instead write y = ++x then x is incremented from 0 to 1, and its result is 1 (the new/current value stored in x) which is stored into y, and this value (1) is the result of the entire expression.

While the prefix/postfix distinction for these operators may seem strange, they are both useful and we will see important uses of each soon.

To illustrate state change operators, we often use before/after pictures (the same kind of pictures used to illustrate variable declarations). For example, we can illustrate the meaning of x=y as follows.

As we have just learned, = is a state change operator: it changes the state of its left operand (which must be a variable) to store the value of its right operand (a value of the same type, or a value derived by implicit conversion); its result is also the value stored. Thus, a expression such as x = x+1 serves to increment the value stored in x by 1 (yes, there are other ways to do this as well).

On the other hand, == is not a state change operator: it compares the two values of its operands (which must be of the same type, but neither has to be a variable), and its result is always of type boolean; it changes neither operand. An expression such as x == x+1 is syntactically legal, but completely useless: it always computes the value false and has no other effect (it changes no states of any variables involved).

Confusing = and == is common. Be on the lookout for such mistakes, which can cause subtle bugs in your programs. In many cases the Java compiler will issue a warning if it suspects you have misused one of these operators (we will see examples in the next lecture)

    int    Math.abs    (int)
    double Math.abs    (double)
    int    Math.min    (int,int)
    double Math.min    (double,double)
    int    Math.max    (int,int)
    double Math.max    (double,double)
    double Math.pow    (double,double)
    double Math.sqrt   (double)
    double Math.log    (double)
    double Math.exp    (double)
    double Math.cos    (double)
    double Math.sin    (double)
    double Math.tan    (double)
    double Math.random ()

• abs returns the absolute value of its operand (overloaded for int and double).
• min returns the minimum of its two operands (overloaded for int and double).
• max returns the maximum of its two operands (overloaded for int and double).
• pow returns the first operand (which must be non-negative unless the second operand is integral: e.g., 3.) raised to the power of the second operand: pow(x,3.5) computes x^3.5 (otherwise returns NaN).
• sqrt returns the square root of its operand (which must be positive, otherwise returns NaN): sqrt(x) is better than pow(x,.5) (faster and more accurate) although both are legal.
• log returns the logarithm (base e) of it operand (which must be positive, otherwise returns NaN).
• exp returns the e raised to the power of its operand.
• cos returns the cosine of its operand (which is expressed in radians, not degrees)
• sin returns the sine of its operand (which is expressed in radians, not degrees)
• random returns a random number in the range [0.,1.); e.g., this semi-open interval specifies that it can return the value 0. but returns a value always strictly less than (never equal to) 1.

The random method is interesting because it is the first one that we have seen whose prototype specifies no operands. Yet, we still must call it with parentheses, as we must for all methods: Math.random(), which will effectively return a different, random, result each time that it is called.

Note that none of these methods are state-change methods; they produce values but do not change what is stored in any variables used as operands. So, given int a = 3, b = 4; then Math.max(a,b) also results in the int 4, and neither a nor b changed: they still store 3 and 4 respectively. In fact, the Java programming language prohibits writing methods that change the states of their operands: this is a bit too subtle to understand here, but we will examine this statement and its ramifications soo.

    void   System.out.print  (int)
    void   System.out.print  (double)
    void   System.out.print  (boolean)
    void   System.out.print  (char)
    void   System.out.print  (String)

    void   System.out.println()
    void   System.out.println(int)
    void   System.out.println(double)
    void   System.out.println(boolean)
    void   System.out.println(char)
    void   System.out.println(String)

Each of the print methods displays a value in the console window and stays on the same line (so any subsequent output will continue to be displayed on that same line). Each of the println methods displays a value in the console window and then goes to the beginning of the next line. In fact, writing just System.out.println() in a program (supplying no operands to the method call) will print nothing and go to the beginning of the next line. So

    System.out.print("A");
    System.out.println("B");
    System.out.println("C");
    System.out.print("D");
    System.out.print("E");

    AB
    C
    DE

We can also accomplish the equivalent by carefully using the newline escape characters: System.out.print("AB\nC\nDE");

We frequently use the catenation operator (which always produces a String) inside these methods: e.g., if we declare int gamesPlayed = 0; and then give the command

  System.out.println("Games Played so far: " + gamesPlayed);

The Prompt class contains a variety of methods for inputing information. The prototypes for the simplest of these methods (there are more) are

    int    Prompt.forInt    (String)
    int    Prompt.forInt    (String,int,int)
    double Prompt.forDouble (String)
    char   Prompt.forChar   (String,String)
    String Prompt.forString (String)

int  cashToBet = Prompt.forInt("Enter amount of Cash to Bet"); 
char action    = Prompt.forChar("Action: w=withdraw d=deposit","wd");

System.out.println('A'+'B');

It is important to get into the habit early of not being shy about running experiments on the computer, even if they are as simple as this one. In fact, thinking of the simplest experiment to perform to check some Java features requires a deep understanding of programming. As I've been learning Java, I've run hundreds of these small experiments (including many for some of the more technical points in this lecture).

• S1: A literal is a legal expression; its type is the type of the literal.
• S2: A variable is a legal expression; its type is the declared type of the variable.
• S3: An operator (or method) whose operands (each of which must be a legal expression) match any of its prototypes (possibly with the aid of automatic conversion) is a legal expression; its type is the result type specified in the prototype.

For each syntax rule there is a companion semantic rule for evaluating expressions.

• E1: A literal evaluates to itself (a trivial but noteworthy rule, for the sake of completeness).
• E2: A variable evaluates to the current value stored in it; remember evaluating expressions with state-change operators can change the values stored in variables.
• E3: An operator (or method)
  • Evaluates each of its operands (which are themselves legal expressions).
  • Performs any implicit conversions (needed to match its prototype).
  • Applies the operator (or method) to its operands to compute its result, which is based on the semantics of that operator/method.

For example, assume that we declare int x = 3; in a program and then want to determine whether the expression 3*x+1 is a legal expression (and what its resulting type and value is). The entier proof follows.

• We can prove that 3 is a legal expression of type int (by S1); its value is 3 (by E1)
• We can prove that x is a legal expression of type int (by S2); its value is 3 (by E2)
• We can prove that 3*x is a legal expression of type int (by S3: we just proved both 3 and x are legal expressions of type int, and one of the prototypes of * is int * (int,int)); its result type is int and its value is 9 (by E3 and applying the semantics of the multiply operator).
• We can prove that 1 is a legal expression of type int (by S1); its value is 1 (by E1).
• Finally, we can prove that 3*x+1 is a legal expression of type int (by S3: we just proved both 3*x and 1 are legal expressions of type int, and one of the prototypes of + is int + (int,int)) ); its rsult type is int and its values is 10 (by E3 again, and applying the semantics of the add operator).

To create an oval diagram, first circle (or draw an oval around) every literal and variable in the expression. These expressions are like atoms in chemistry: they contain no smaller constituents. Next, label their types on top and label their values (if you know them) on the bottom. Then, draw an oval around each operator (or method) and its operands; label the type with the result type of the matching prototype for that operator, and label the bottom with the result value (if you know how to compute it from its semantics).

Note that even if we do not know the values stored in variables, we can still produce an oval diagram that verified the legality of an expression; we just cannot determine what value it computed. The outermost oval is labelled by the type of the entire expression. Here is an example of an oval diagram for the previously discussed expression: 3*x+1

++ --

+ - ! ++ --

(type)expression

* / %

+ -

< <= > >=
instanceof

== !=

&&

||

= += -= *= /= %=

The rules for using these tables on expressions are

• O1: When an expression contains two consecutive operators, neither appearing in parentheses, Java applies the higher precedence operator first.
• O2: When an expression contains two consecutive operators, neither appearing in parentheses, and both have the same precedence, Java applies left associative operators left to right and it applies right associative operators right to left.
• O3: Java always evaluates expressions in parentheses before it uses them as operands in other expressions (so we can use parentheses to override precedence, forcing the operators inside the parentheses to be evaluated before the operators outside the parentheses).
• O4: Java always evaluates the operands of a method, in a left-to-right order, before it applies the method (computes the method's result).

In the expression below 3*(x+1) the subexpression x+1 appears in parentheses. Again, we start by circling all literals and variables. Then we see two consecutive operators, but this time the second one is in parentheses. By rule O3, we must handle all the operators inside the parentheses first (circling the + operator first) and then circling the * operator last, after its operand has been circled. This complete this oval diagram.

In fact, the parentheses themselves are suggestive of two sides of an oval; you can always draw ovals around parenthesized expressions: they can be used to represent the result computed by the last operator inside the parentheses.

Next, examine the following four expression that each attempt to compute the volume of a sphere with radius r. The only difference among these expressions are the types of the literals used (the ones without decimal points are int and the ones with decimal points are double). Assume that we have already declared double pi = 3.1416;

    4./3.*pi*Math.pow(r,3.)                 4./3*pi*Math.pow(r,3.)
    4 /3.*pi*Math.pow(r,3.)                 4 /3*pi*Math.pow(r,3.)

Thus, we can use oval diagrams not only to compute the type/value of an expression, we can use them to debug incorrectly formed expressions.

For example, it is sometimes the case that a program declares a few int counters, and then must compute ratios of these counters; to avoid the truncation that occurs with int division, we can explicitly convert an int value into a double. For example, suppose that we declared int attendance = 78, capacity = 100; Writing

  (double)attendance/(double)capacity

Note that (double)(attendance/capacity) does NOT do the job. It first performs integer division, so it is equivalent to (double)(0) whose result is 0.

Sometimes casts are necessary to satisfy syntax constraints. Suppose that we wanted to generate a random integer between 1 and 6 and store it in the variable named choice. We CANNOT write int choice = 1 + 6*Math.random(); In this expression Java would implicitly convert 6 to a double to perform the multiplication (returning a double result), and then Java would implicitly convert 1 to a double to perform the addition (returning a double result); finally, we cannot store a double value into an int variable.

Instead, we can write this expression correctly as int choice = 1 + (int)(6*Math.random()); In this case, the compiler will report no syntax constraint error because we have explicitly casted (6*Math.random()) to an int Thus, the value ultimately stored in choice is a integer from 1 to 6 inclusive. Casting does not change the values stored in any variables.

Write an oval diagram for the expression above, and compute the result stored into choice for different random numbers between 0 (which can be generated) and 1 (which cannot be generated); try a few values including 0 and something a tad less than 1. Use other oval diagrams to understand why 1 + 6*(int)Math.random() and 1 + (int)6*Math.random() do not always compute correct results. Does (int)(1 + 6*Math.random()) work; use an oval diagram to find out.

• Suggestive Spacing: use extra whitespace around lower-precedence operators to suggest that they are evaluated later. Recall that whitespace doesn't change the meaning of a program (all the tokens remain the same).
• Redundant Parentheses: use unneeded parentheses (they do not override the precedence of any operators) around higher-precedence operators to suggest that they are evaluated earlier.

Expression	Suggestive Spacing	Redundant ()
.5*A*T*T+V*T+D	.5*A*T*T + V*T + D	(.5*A*T*T)+(V*T)+D

Also, use literals of the correct type to avoid implicit conversion (which often leads to hard-to-find errors). If you want conversion to occur, use casting to make it explicit: doing so doesn't change how Java evaluates the expression (implicit conversion and casting both do the same thing) but for anyone reading the program, the expression will be easier to understand. You can check the expressions you write by analyzing them with oval diagrams, evaluating them for a few different values to ensure that they compute the right answers.

Don't cast literals; when I see students write (double)5 it pains me greatly: use 5. instead.

If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a CA, a Tutor, or any other student.

1. Show a few different ways to declare A and B as int variables initially storing 0 and 1 respectively. Do it with one declaration statement; with two declaration statments; write slightly different variants of these that still accomplish the job.

2. Both of the following are illegal declarations (according to EBNF)

     int x = 0, boolean isOK = false;
     int x = y = 0;

   Explain why. Write legal declarations that accomplish what these are trying to do.

3. Write prototypes for each of the following methods. Infer the information needed in the prototype from each function's description.
   • countPrimesBetween returns the number of primes occuring between two integers: e.g., countPrimesBetween(11,24) evaluates to 5, because 11, 13, 17, 19, and 23 are prime.
   • distance returns the euclidean distance between two points in the plane (each point is represented by two doubles).
   • inSameQuandrant returns whether or not two points lie in the same quadrant (each point is represented by two doubles).
   • shuffle returns the interleaved characters from its operands: shuffle("abcd","efgh") returns "aebfcgdh".

4. What are the results of each of the the following operators?

       7/10   7./10   7/10.   7./10.
       7/10   57/10   157/10   2157/10
       7%10   57%10   157%10   2157%10

5. Show the result produced by each of the following operators/methods (or indicate that some syntax error is present). If the state of some variable is changed, show that too (and indicate any implicit conversions). Assume int x = 0; String s = "ABC"; before each call

     false == false          'a' < 'Z'          'a'-'A'
     true  != true           true && false      true || false
     x++                     ++x                1 = x
     x = 1                   x == 1             x = 'A'
     Math.abs(-3.5)          Math.abs(3.5)      Math.max(3.5, 8)
     Math.sqrt(-1.)          Math.pow(-3.,2.)   Math.pow(-3.,.5)
   
     s = System.out.println("Hi");
   

6. Assume that we declare int a = 1; What would be stored in a after evaluating a = a++? What would be stored in a after evaluating a = ++a? What do you think the programmer is trying to accomplish? What is an easy way to accomplish it?

7. What is printed in each of the following method calls.

     System.out.println("" + 1 + 1 + 1);
     System.out.println(1 + 1 + 1 + "");
     System.out.println('1' + 1 + "");

8. Analyze each of the following expressions, assuming int a=1,b=2; and write an oval diagram for each.

         (a+b)/2       a+b/2
         100.*a/b      100.*(a/b)      a/b*100.

9. Assume that we declare double a,b; evaluate the expression (a+b - Math.abs(a-b))/2. when
   • a stores 3. and b stores 5.
   • a stores 5. and b stores 3.
   Try a few other example values for a and b. Describe in general terms what this expression evaluates to.

10. Assume that we declare int a,b; also assume that the method whose prototype is int Util.characteristic(boolean) returns 1 if its operand is true and 0 if its operand is false. Evaluate the expression
        Util.characteristic(a<b)*a+Util.characteristic(a>=b)*b
    when
    • a stores 3 and b stores 5.
    • a stores 5 and b stores 3.
    Try a few other example values for a and b. Describe in general terms what this expression evaluates to.

11. Translate each of the following mathematical formulas (7 on the top line, 3 on the middle and bottom lines) into Java expressions. Assume that all variables (some have subscripts) are declared to be of type double. Writing |x| means the absolute value of x. Analyze each expression by writing its oval diagram.
    

12. Suppose that we declare int attendance = 3000, capacity=10000; the number of fans attending an event at a stadium and the maximum number of fans possible at that stadium respectively. Which of the following Java expressions evaluates to 30, the percentage of fans in the stadium? What do the "incorrect" expressions evaluate to?

            attendance/capacity
            100*attendance/capacity
            100*(attendance/capacity)
            attendance/capacity*100        

13. The expression x < 10 && y does not compute whether x is less than both 10 and y. Show that the syntax of this expression is incorrect; how far can Java get before it discovers the error? Find a way to correctly test if x is less than 10 and x is less than y. Assume we declare int x = 50, y = 20; Draw an oval diagram that shows what value Java computes for your expression (it should evaluate to false, because x is not less than y: is that what it computes?).

14. Assume that we declare int x; Write an expression whose result is X rounded to the nearest 10: e.g., if x were 1432 the result would be 1430; if x were 1437 the result would be 1440; if x were 1435 round up so the result would be 1440 also. Use only the standard arithmetic operators and casting.

15. Assume that we declare double x; Write an expression whose result is the int value closest to x: e.g., if x were 3.2 the result would be 3; if x were 3.9 the result would be 4; if x were 3.5 round up so the result would be 4 also. Just casting doesn't work, because of truncation: 3.9 would be cast to 3.

16. Assume that we declare int year; Write an expression whose result is true whenever year stores a leap year and false otherwise. We define a leap year as any year that is a perfect multiple of of 4, but not if it is a perfect multiple of 100 (unless it is also a perfect multiple of 400). Note that one number is a perfect multiple of another if the remainder after division equals zero.

17. Assume that we declare int a = 2, b = 5; What are the values of a, b, and the entire expression, after evaluating the expression a+++b; the same question, but for the expression a+ ++b?

18. Assume that we declare int x,y,z; Write an expression that computes whether...
    • ...x is odd
    • ...x is a multiple of 20 (e.g., 20, 40, 60, ...)
    Assume that zero is a positive number. Write an expression that computes whether...
    • ...x and y are both positive
    • ...x and y have the same sign (both are positive or both are negative)
    • ...x and y have different signs (one is positive and one is negative)
    Write an expression that computes whether...
    • ...all three variables (x, y, and z) store the same value
    • ...all three variables (x, y, and z) store different values (none the same)
    • ...two variables store the same value, but the third one is different

19. Assume that we declare char c; Write an expression that evaluates to true when c stores...
    • ...a lower-case letter
    • ...a lower-case or upper-case letter
    • ...a character that is a digit
    • ...an upper-case vowel

20. Assume that we specify two points in the place with the declaration double x1,y1, x2,y2; Write an expression that computes...
    • ...the distance between these points
    • ...the slope of the line from the first point to the second
    • ...whether both points lie on the same line from the origin
    • ...whether the first point is above the second
    • ...what quadrant the first point lies in (1st, 2nd, 3rd, or 4th)
    • ...whether the two points lie in the same quadrant

21. Assume that we specify a circle with the declaration double centerX, centerY, radius; and a point by the declaration double x,y; Write an expression that computes whether or not the point lies inside the circle (including the boundary).

22. Assume that specify an interval by a pair of int values (the ones at the beginning and end of the interval in the place with the declaration): 5 and 8 would specify the interval containing the numbers 5, 6, 7, and 8 inclusive. We declare int b1,e1, b2,e2; to represent the beginning and end of two intervals, and int x; so represent some value. Note that we will guarantee that the intervals are "well formed": b1 <= e1 and b2 <= e2.
    • Write an expression that computes the number of values in an interval beginning with b1 and ending with e1.
    • Write an expression that computes whether...
      • ...x is inside the first interval
      • ...x is not inside the first interval
      • ...x is inside the first interval but not the second
      • ...x is inside either the first or second interval (or both)
      • ...x is inside either the first or second interval (but not both)
    • Write an expression that computes whether...
      • ...the first interval is the same as the second
      • ...the first interval ends before the second one begins
      • ...the first interval ends on the same value as the second one begins
      • ...the first interval is inside the second one
      • ...the first interval and the second interval overlap (at least one common value)
      • ...the first interval and the second interval do not overlap (no common values)
    Draw pictures to help you visualize the relationships; choose your relational and logical operators carefully, and try a few examples to convince yourself that your expressions are correct. For example, the following picture shows the first interval inside the second.
    

23. Assume that we declare int x,y,z; Write an expression that computes the minimum of these three values. You may use the Math.min method.

24. Assume that we declare char d; and guarantee that it stores a character corresponding to a digit: '0', '1', '2', ... '9'. Write an expression that computes the int equivalent to that value: 0 for '0', 1 for '1', etc. Note that (int)d converts the char to an int, but not the right one: e.g., by the ASCII table (int)'0' results in 48, (int)'1' results in 49, ... (which should give you a clue)

25. Assume that we declare char c; and guarantee that it stores a character corresponding to a lower-case letter: 'a', 'b', 'c', ... 'z'. Write an expression that computes the upper case equivalent to that value: 'A' for 'a', 'B' for 'b', etc. Eventually, you must use casting.

26. Assume that we declare int low, high, x; and that we guarantee that low <= high. Write an expression whose result is low if x is smaller than low, high if x is greater than high, and x if it is between these values. You may use the Math.min and the Math.max methods.