15-105 SPRING 2009 [CORTINA]
HOMEWORK 10 - due Wednesday, April 22
WRITTEN PROBLEMS (8 pts)
Hand these problems in on paper in class on the due date specified.
- (1.5 pts)
A parallel processor has three processors, each running a computation at
the same time that includes the following instructions which all
reference the same variable X. No other instruction changes the variable
X. (^ represents exponentiation: X^3 means X3.)
PROCESSOR 1 PROCESSOR 2 PROCESSOR 3
----------- ----------- -----------
: : :
: : :
X <-- X + 3 X <-- X * 3 X <-- X ^ 3
: : :
: : :
-
Assuming that each instruction is "atomic", how
many different outcomes can we have for the variable X after all
processors are finished? (Remember, each processor may not get to its
specified instruction at the same time.)
-
What is the final value of X for each of the possible outcomes from part
(a) assuming X starts out with the value 2 before the processors compute
in parallel?
-
What does it mean for an instruction to be "atomic"?
- (1 pt)
A computation on a single processor takes 8 minutes (480 seconds).
-
If this computation were performed on a parallel processor with 12
processors of the same speed as the original single processor,
what is the fastest this computation could be performed,
ignoring any overhead required to split the computation to run in
parallel? Explain your answer.
-
If 1/4 of this computation must be performed sequentially (i.e. not
in parallel), how long will this computation take according to
Amdahl's Law on a parallel processor with 12 processors of the same
speed as the original single processor?
Show your work.
- (1 pt)
At a furniture factory, a bookcase is manufactured using the following
four steps in sequence:
1. Cut the wood pieces (30 minutes)
2. Sand and stain the wood pieces (50 minutes)
3. Drill pilot holes for all screws (10 minutes)
4. Screw pieces together to assemble bookcase (20 minutes)
-
If one bookcase is made at a time, and the factory wants to make 600
bookcases, how many minutes would it take to complete this task?
-
If the factory utilized pipelining and had four work stations, one for
each step above, how many minutes would it take to complete this task?
Show your work.
- (1 pt)
In class, we saw how a pipeline can be used to perform matrix
multiplication. Suppose we want to compute the average for a class of 1000
students and the class consists of 10 graded items. Each multiply-add
operation is one multiplication and one addition.
-
How many muliply-add operations are required to compute the results
sequentially without pipelining?
-
If we use pipelining, how many multiply-add operations do we save?
Explain your answer.
- (1.5 pts)
A computational unit for a concurrent network is
shown below. Its top output is the sum of its inputs.
Its bottom output is the difference of its inputs. The
concurrent network also shown below is made up of 12 of these
computational units. (A network like this is used to
compute the Fast Fourier Transform, which is used
in applications such as digital signal processing for music.)
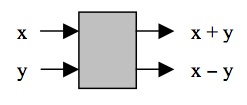
A single computational unit.
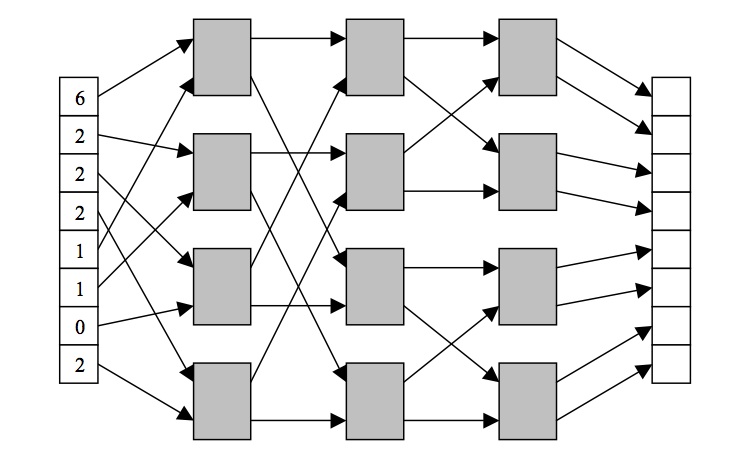
A network of computational units.
-
Using the data shown at the left, what is the data that will be stored at
the right? Show your work.
-
If each computational unit takes time t to compute its output, how long
does it take to compute the final output of this network concurrently?
Explain.
-
If we wanted to use this network for 10 sets of 8 data values, what is the
minimum amount of time that it will take to compute the final output for
all 10 sets of data based on your answer in part (b)? (HINT: Think
pipelining!)
- (2 pts)
In class, we discussed a situation called deadlock which can cause
a system to stop functioning.
-
Consider a main road (shown running left to right) with two side roads.
All roads have single lanes in each direction.
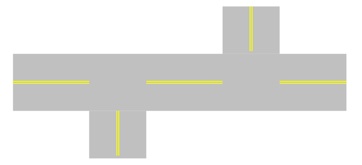
Explain how deadlock can occur on the main road. Draw a picture to help
illustrate your answer.
-
Consider two programs running simultaneously, each wanting access to
the same two databases. When a program
accesses one database, it locks it so another program cannot use it.
Once the program is done using the database, it unlocks the database.
If a program tries to access a database and it is locked, it waits
until it is unlocked.
Explain how deadlock can occur for these two programs.
COMPUTER PROBLEM (2 pts)
Hand this in electronically using the
Electronic Handin System by 11:59PM on the due
date indicated.
Last week, you started work on the
Line 'Em Up game which consists of a 3 X 6 grid of circles of 6
colors, 3 of each. The
goal is to rotate the lights horizontally and vertically until every
column has a light of a
single color. A sample game board is shown below. Note that there is an
extra row and column in the game window.

In this problem, you will complete the Python program so it plays the
game correctly. Start with the following Python program
(right-click HERE for a copy on your computer):
# lineemup.py
# Program that plays a Line 'Em Up game
from graphics import *
def main():
filename = raw_input("Input name of data file: ")
window = GraphWin("Line 'Em Up", 350, 200)
colorarray = initialize_array(filename)
draw_lines(window)
display_circles(window,colorarray)
game_over = False
while game_over == False:
p = window.getMouse()
column = p.getX()/50 # compute column where player clicked
row = p.getY()/50 # compute row where player clicked
update_array(colorarray, row, column)
display_circles(window,colorarray)
game_over = check_for_winner(colorarray)
print "GAME OVER"
raw_input("Press <ENTER> to quit.")
window.close()
def initialize_array(filename):
infile = open(filename, "r")
colorarray = []
for i in range(3):
colorarray.append([])
for row in range(3):
for column in range(6):
colorvalue = eval(infile.readline())
colorarray[row].append(colorvalue)
return colorarray
def draw_lines(window):
for i in range(6):
line = Line(Point(50*(i+1),0),Point(50*(i+1),200))
line.draw(window)
for j in range(3):
line = Line(Point(0,50*(j+1)),Point(350,50*(j+1)))
line.draw(window)
def display_circles(window,colorarray):
colors = ["blue","green","cyan","red","magenta","yellow"]
for row in range(3):
for column in range(6):
center = Point(column*50+25,row*50+25)
circ = Circle(center,20)
circ.setFill(colors[colorarray[row][column]])
circ.draw(window)
def update_array(colorarray,row,column):
# to be completed by you
return # remove this line when you complete this function
def check_for_winner(colorarray):
# to be completed by you
return False # remove this line when you complete this function
main()
When the player clicks in one of the first six empty boxes along the
bottom, you will rotate that column of the board one position
UP
(moving the first color into the last position of that column). When the
player clicks in one of the first three empty boxes along the right, you
will rotate that row of the board one position to the
LEFT (moving the
first color into the last position of that row). Nothing happens if
a player clicks the empty box in the bottom right or on any box with a
circle.
You will need to complete the two functions: update_array
and check_for_winner.
The update_array function follows the following algorithm (read
carefully):
1. If row = 3 and column ≠ 6 do the following:
a. Set temp equal to colorarray[0][column].
b. For i in the range 0 to 1, do the following:
i. Copy colorarray[i+1][column] into colorarray[i][column].
c. Set colorarray[2][column] equal to temp.
2. If column = 6 and row ≠ 3 do the following:
a. Set temp equal to colorarray[row][0].
b. For i in the range 0 to 4, do the following:
i. Copy colorarray[row][i+1] into colorarray[row][i].
c. Set colorarray[row][5] equal to temp.
The check_for_winner function should return True if each column
contains only one color. Use this algorithm:
1. Set column = 0.
2. While column < 6, do the following:
a. If colorarray[0][column] ≠ colorarray[1][column], return False immediately.
b. If colorarray[1][column] ≠ colorarray[2][column], return False immediately.
c. Add 1 to column.
3. Return True.
NOTE: When you use the return instruction in a function in
Python, it returns immediately to the calling function without completing
the rest of the current function.
Use the data file from homework 9 to test your game.



