15-121 SPRING 2010 [CORTINA]

HOMEWORK 5 - due Tuesday, February 23

WRITTEN PROBLEMS (10 points)

(1 pt) Recall in class that the SinglyLinkedList class consists of a reference to the head of the list only. If the list has n nodes, adding or removing from the end of the list takes O(n) time since you have to traverse the entire list to find the last node. Suppose we store references to the head and tail of the list instead of just the head of the list. What is the worst case runtime complexity for adding to the end of the list and removing from the end of the list as a function of n? Explain.
(1.5 pts) Let the DoublyLinkedList<E> class represent a doubly linked list with a reference to the head node and a reference to the tail node, both of type Node<E>. Each node has a data field of type E and two Node<E> references named prev and next. The Node<E> class is defined as an inner class of DoublyLinkedList<E>. Write a method for this class named remove that takes an index of a node of the list and removes the node from the list and returns a reference to its data. A valid index is between 0 and the size of the list minus 1. If the index is invalid, throw an exception instead.
(1.5 pts) Consider a variant of the singly linked list that contains a "dummy node" at the beginning of the list with no data (i.e. the data field is always null). An empty list consists of a dummy node only. A list with n elements has n+1 nodes, the first node being the dummy node. The dummy node makes it easier to implement add and remove operations since the list can never be truly empty.
1. Rewrite the constructor for SinglyLinkedList so it creates an "empty" list consisting of one dummy node.
2. Rewrite the methods add and remove assuming the singly linked list always contains a dummy node.
(1.5 pts) Write a Java method that prints out the contents of a singly-linked list in reverse order using O(1) additional storage. You may assume that this method is part of the SinglyLinkedList class. When we say "using O(1) additional storage", we mean that the amount of extra memory used is not dependent on the size of the list. Explain why your method only uses a constant amount of extra storage space. What is the runtime complexity of your algorithm using big-O notation in terms of n? Justify your answer.
Special note to those who know about recursion: This method should not be recursive because recursion requires the use of the system stack which will grow proportionally to the size of the linked list.
(1 pt) See the description of a sparse matrix in the programming assignment below. Assume that each int takes 4 bytes and each object reference takes 8 bytes. You want to store an 200 × 200 matrix using either a two-dimensional array or a sparse matrix as defined below. A two-dimensional array stores its values in sequential memory locations row by row with no additional memory required. What is the maximum number of nonzero values that can be stored in the matrix so that the sparse matrix uses less memory than the two-dimensional array? Show your work.
(1 pt) Smithers decides to implement his own stack, called SmithersStack<E>. The contents of the stack are stored in a field called data of type ArrayList<E>, where INDEX 0 represents the TOP of the stack.
```
public class SmithersStack<E>
{
        private ArrayList<E> data;  //top element at index 0

        //constructors and other methods not shown
}
```
1. Complete the pop method for the SmithersStack class and determine the worst-case runtime complexity of pop assuming that the stack contains n elements. If the stack is empty, return null in this case.
2. Complete the push method for the SmithersStack class and determine the worst-case runtime complexity of push assuming that the stack contains n elements.
(1 pt) Complete the method below, which should return a new stack containing the playing cards in the given stack in the same order, with all aces removed.
```
public static LIFOStack<PlayingCard> removeAces(LIFOStack<PlayingCard> s)
{

}
```
(1.5 pts)
1. The infix-to-postfix converter discussed in class translates an infix expression to the equivalent postfix expression using a stack. Convert the following infix expression to a postfix expression and show the contents of the stack (from top to bottom) and the resulting postfix string after each operator is processed.
```
4 + 3 + ( 7 - 4 / 2 ) * 5 - ( ( 2 + 1 ) * 6 ) * 9 - 8
```
2. The postfix evaluator discussed in class computes the value of any valid postfix expression using a stack. What is the value of the following postfix expression? Show the contents of the stack (from top to bottom) after each operator is processed.
```
8 6 3 4 + * 2 / 5 3 * - +
```
3. If the postfix evaluator is given an expression that is not a valid postfix expression, the algorithm will fail to give a correct answer. Give an example of each case where the algorithm might fail and explain why it fails.

PROGRAMMING PROJECT (10 points)

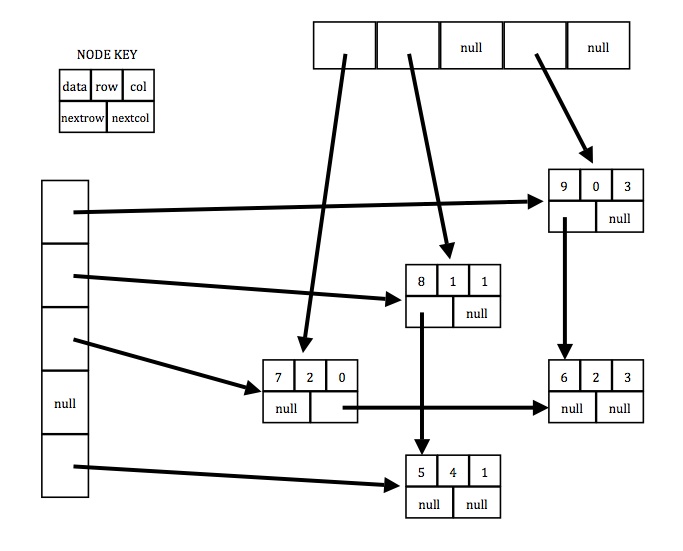
A sparse matrix is a 2-dimensional array where a large portion of the array stores no data. For example, this 5 × 5 integer matrix could be considered sparse assuming we only store positive integers in the matrix:

Instead of storing a sparse matrix using a two-dimensional array, we can store this using linked lists where we only store nodes for the locations that have non-zero values. The sparse matrix above would be stored as shown in the picture below:

Assignment

Download the project file SparseMatrix.zip. In this project, you should complete the class SparseMatrix that implements a sparse matrix of integers using linked lists. Each positive value of the matrix is stored using a node that has a field for the data value, fields to store the location of the value in the matrix (row and column), and fields for references to the next node in the same row and same column. Remember that only non-zero values are stored in nodes in the data structure. All "missing" nodes represent locations in the matrix where the data value is 0.

The sparse matrix contains two arrays of references to the heads of the lists of nodes for rows and columns. (See the picture above.)

Programming Requirements

Implement the SparseMatrix class based on the javadoc file SparseMatrix.html and the information below. DO NOT CHANGE ANY CODE ALREADY GIVEN TO YOU.

Your class should contain an inner class to represent a node for this sparse matrix. You will need two constructors: one which contains parameters for the data value, row and column numbers, and another that has no parameters (default).
The constructor should create two arrays to hold the references to heads of the row lists and column lists. If the supplied number of rows or columns is invalid, assume the matrix is 5 × 5 by default. It is assumed that the initial sparse matrix stores only zeroes.
CAUTION: When you create your arrays to hold the references to the head of each row and column, do NOT create an array of LinkedList of generic type Node. What this does is create separate linked lists for the rows and columns, where each node of the linked list stores a Node object. Instead, your array should hold references to Node objects directly. Do NOT use the LinkedList class in the Java API.
The set method should add a node (if necessary) to the list structure if the supplied value is positive or remove a node (if necessary) from the list structure if the supplied value is zero. If the supplied value is negative, do not change the matrix. If the given row or column is invalid, do not change the matrix. You will want to write helper methods, as this is not a trivial method! Think about this method carefully before you start coding.
The getByRow method gets the value in the matrix at the given row and column by traversing the matrix along the list corresponding to the given row. (Of course, if the required node is not in the list, then the value must be 0.)
The getByColumn method gets the value in the matrix at the given row and column by traversing the matrix along the list corresponding to the given column.
The getNumElementsInRow method returns the number of nodes in the list corresponding to the given row in the matrix. This should correspond to the number of non-zero elements in that row. You must traverse the list and count all of the nodes in the given list. You cannot just keep track of this value in a variable/array and return it. This method is checking to see if your list is set up correctly.
The getNumElementsInColumn method returns the number of nodes in the list corresponding to the given column in the matrix. This should correspond to the number of non-zero elements in that column. You must traverse the list and count all of the nodes in the given list. You cannot just keep track of this value in a variable/array and return it. This method is checking to see if your list is set up correctly.
The transpose method creates and returns a new sparse matrix that is the transpose of the current matrix. The transpose of an m × n matrix A is an n × m matrix B such that B[i, j] = A[j, i] for 0 ≤ i ≤ n-1 and 0 ≤ j ≤ m-1. For example, the transpose of the matrix
```
1 2 3 4
5 6 7 8
```
is the matrix
```
1 5
2 6
3 7
4 8
```
Your transpose method should create the new matrix by scanning across each row list in your current matrix and using your set method to add each nonzero value to a new matrix in its correct position.
The methods getNumRows and getNumColumns are self-explanatory.

Helpful Programming Advice

It is much easier to write a little code and debug, repeating many times, than it is to write many lines of code and then debug. If you have partially complete but working program, you will receive more credit, than a complete program that is not working. Therefore, we suggest the following strategy for this assignment:

Start by only considering row links only. Write set to handle non- zero values, getNumRows, getNumColumns, getByRow, and getNumElementsInRows. Write stubs for remaining methods. Develop test cases and test.
Now update set to consider the column links for non-zero elements. Complete getByCol and getNumElementsInColumn. Test.
Update set to handle zero values. Add test cases and test.
Write and test transpose.

As you complete each step, save your work elsewhere. This way, if you really get stuck and run out of time, you can restore a previous version that partially works to maximize your partial credit.

Debugging/Testing

Supplied in your project file is SparseMatrixTester.java which contains a simple program to test the functionality of your data structure. Add comments to the tester to explain what each part is doing. Explain why the try/catch blocks are needed. (Don't say: "because an exception could be thrown". Explain what can go wrong specifically to cause the exception to occur.)

When you run the program, it will ask you to enter a data value, row and column. It will then try to set that row and column in the sparse matrix to the given value. It will then display the matrix by scanning each row first, then again by scanning each column to see if all of your links are correctly maintained. Additionally, it will display a number in square brackets at the end of each row and bottom of each column to tell you how many nodes you have in each list. These numbers should correspond to the number of nonzero values in each list. For example, here is the output after storing the value 2 in row 1 column 0 in a 4 × 3 matrix originally containing only zeroes (user input in italics):

SPARSE MATRIX TESTER
At each prompt, input a triple: data row column
For example, to set row 2 column 1 to the value 43,
you would input 43 2 1
Input -1 -1 -1 to exit input loop.
Once you exit input loop, the transpose will be displayed.
Input number of rows for sparse matrix: 4
Number of rows: 4
Input number of columns for sparse matrix: 3
Number of columns: 3
Sparse Matrix by Rows:
0	0	0	[0]
0	0	0	[0]
0	0	0	[0]
0	0	0	[0]
[0]	[0]	[0]	
Sparse Matrix by Columns:
0	0	0	[0]
0	0	0	[0]
0	0	0	[0]
0	0	0	[0]
[0]	[0]	[0]	

Input: 2 1 0
Storing 2 in row 1 column 0
Sparse Matrix by Rows:
0	0	0	[0]
2	0	0	[1]
0	0	0	[0]
0	0	0	[0]
[1]	[0]	[0]	
Sparse Matrix by Columns:
0	0	0	[0]
2	0	0	[1]
0	0	0	[0]
0	0	0	[0]
[1]	[0]	[0]	

Input: -1 -1 -1

The TRANSPOSE of your matrix is: 
Sparse Matrix by Rows:
0	2	0	0	[1]
0	0	0	0	[0]
0	0	0	0	[0]
[0]	[1]	[0]	[0]	
Sparse Matrix by Columns:
0	2	0	0	[1]
0	0	0	0	[0]
0	0	0	0	[0]
[0]	[1]	[0]	[0]

The two matrix outputs should always match, but each is generated using different methods of your SparseMatrix class.

TESTING USING THE COMMAND LINE: A way to speed up your testing is to run your program from the command line rather than through Eclipse. (You can still use Eclipse to edit the file.) On the LINUX terminal, open the Terminal application and go to the directory that contains your source code. For example, if your workspace is on your desktop, then you would type:

cd Desktop/MyWorkspace/SparseMatrix/src

If you then type ls, you can list your files in that directory (folder) and you should see the java files. To compile your program, type

javac *.java

If you see compiler errors, then go back and edit your Java file. If you get the OS command prompt back without errors, you should be able to run your program. To run it, type

java SparseMatrixTester

Now, to speed things up, instead of entering each set of data values from the keyboard each time you run the program, you can store all of the inputs in a text file in the same order as you would type them in at the keyboard. For example, for the example above, your data file should look like this:

Then, when you run the program, you can redirect the data in the file into your program as keyboard input as follows:

java SparseMatrixTester < datafile.txt

This should make debugging faster since you can just examine your output for correctness. If you take 15-211, you will learn a more sophisticated way to test your code using unit testing with JUnit.

You can also cut and paste your data file into the Console area in Eclipse when you run the program.

Documentation & Style

You should add javadoc-style comments to your SparseMatrix class to match the comments given to you in the supplied html file. Make sure you document your code carefully, especially the set method, to explain what you are doing. Use accepted Java programming style throughout your code.

Hand-In Instructions & Late Submissions

Your submitted zip file should include the complete Java program (all Java files). Double-check your zip file before you submit to make sure all of your code is there.

See the course website for instructions on how to hand in your program and the policy for late submissions.