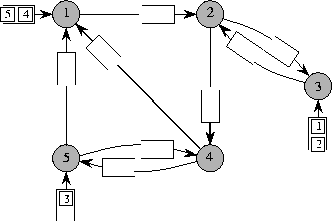
Figure 1: A graph model for packet routing.
Packet routing plays a central role in the design of large-scale parallel computers. Simply stated, packet routing consists of moving packets of data from one location to another in a network. The goal is to move all of the packets to their desired locations as quickly as possible, and with as little queuing as possible. The packet routing problem has been extensively studied, and we refer the reader to [5] for a broader coverage of the topic.
The method of packet routing considered in this paper is known as store-and-forward routing. In a store-and-forward routing algorithm, packets are viewed as atomic objects. At each step, a packet can either wait in a queue or jump from one queue to another.
Figure 1 shows a graph model for store-and-forward routing. The shaded nodes labeled 1 through 5 in the figure represent processors or switches, and the edges between the nodes represent wires. A packet is depicted by a square box containing the label of its destination. The goal is to route the packets from their origins to their destinations via a series of synchronized time steps, where at each step at most one packet can traverse each edge.
Packets wait in three different kinds of queues. Before the routing begins, packets are stored at their origins in special initial queues. For example, packets 4 and 5 are stored in the initial queue at node 1. When a packet traverses an edge, it enters the edge queue at the end of that edge. A packet can traverse an edge only if at the beginning of the step the edge queue at the end of that edge is not full. In the example of Figure 1 the edge queues can hold two packets. Upon traversing the last edge on its path, a packet is removed from the edge queue and placed in a special final queue at its destination. For simplicity, the final queues are not shown in Figure 1. Independent of the routing algorithm used, the size of the initial and final queues are determined by the particular packet routing problem to be solved. Thus, any bound on the maximum queue size required by a routing algorithm refers only to the edge queues.

Figure 1: A graph model for packet
routing.
This paper focuses on the problem of timing the movements of the packets along their paths. A schedule for a set of packets specifies which move and which wait at each time step. Given any underlying network, and any selection of paths for the packets, our goal is to produce a schedule for the packets that minimizes the total time and the maximum queue size needed to route all the packets to their destinations.
Of course, there is a strong correlation between the time required to route the packets and the selection of the paths. In particular, the maximum distance, d, traveled by any packet is always a lower bound on the time. We call this distance the dilation of the paths. Similarly, the largest number of packets that must traverse a single edge during the entire course of the routing is a lower bound. We call this number the congestion, c, of the paths. For example, see Figure 2.
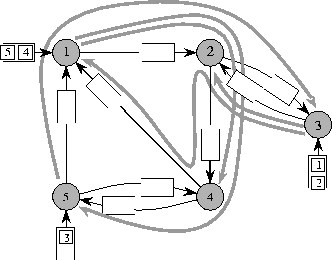
Figure 2: A set of paths for the
packets with dilation d=3 and congestion c=3.
Given any set of paths with congestion c and dilation d in any network, it is straightforward to route all of the packets to their destinations in cd steps using queues of size c at each edge. Each packet can be delayed at most c-1 steps at each of at most d edges on the way to its destination (since the queues are big enough so that packets can never be delayed by a full queue in front.)
In this paper, we show that there are much better schedules. We begin
in Section 2 with a randomized on-line algorithm that
produces a schedule of length ![]() using queues of size
using queues of size
![]() , where N is the total number of packets. This
algorithm is close to optimal when c is large. Our main
result appears in Section 3. It establishes the
existence of a schedule using
, where N is the total number of packets. This
algorithm is close to optimal when c is large. Our main
result appears in Section 3. It establishes the
existence of a schedule using ![]() steps and constant-size queues at
every edge, thereby achieving the naive lower bounds for any routing
problem.
steps and constant-size queues at
every edge, thereby achieving the naive lower bounds for any routing
problem.
The proof of the main result is nonconstructive. However, the result
still has several applications, as described below. In addition, the
result is highly robust in the sense that it works for any set of
edge-simple paths and any underlying network. (A priori, it would
be easy to imagine that there might be some set of paths on some
network that required more than ![]() steps or nonconstant
queues to route all the packets.) Furthermore, the main result can be
made constructive using the recently discovered algorithmic version of
the Lovász Local Lemma [1, 2]. A
manuscript describing the algorithm is in preparation [7].
steps or nonconstant
queues to route all the packets.) Furthermore, the main result can be
made constructive using the recently discovered algorithmic version of
the Lovász Local Lemma [1, 2]. A
manuscript describing the algorithm is in preparation [7].
If a particular routing problem is to be performed many times over,
then the time required to compute the optimal schedule once becomes
less important. This situation arises in network emulation problems.
Typically, a guest network G is emulated by a host network H by
embedding G into H. (For a more complete discussion of emulations
and embeddings, see [3].) An embedding maps
nodes of G to nodes of H, and edges of G to paths in H. There
are three important measures of an embedding: the load, congestion,
and dilation. The load of an embedding is the maximum number
of nodes of G that are mapped to any one node of H. The
congestion is the maximum number of paths corresponding to edges of
G that use any one edge of H. The dilation is the length
of the longest path. Let l, c, and d denote the load,
congestion, and dilation of the embedding. Once G has been embedded
in H, H can emulate G in a step-by-step fashion. Each node of
H first emulates the local computations performed by the l (or
fewer) nodes mapped to it. This takes ![]() time. Then for each
packet sent along an edge of G, H sends a packet along the
corresponding path in the embedding. Using the main result of this
paper, routing the packets to their destinations takes
time. Then for each
packet sent along an edge of G, H sends a packet along the
corresponding path in the embedding. Using the main result of this
paper, routing the packets to their destinations takes ![]() steps.
Thus, H can emulate each step of G in
steps.
Thus, H can emulate each step of G in ![]() steps.
steps.
In a related paper, Leighton, Maggs, Ranade, and Rao
[6] show how to route packets in ![]() steps using a simple randomized algorithm provided that the underlying
network is leveled and has depth L. As a consequence, optimal
routing algorithms can be derived for most of the networks that are
commonly used for parallel computation. Unfortunately, it seems to be
difficult to extend this result to hold for all networks. In fact, we
have considered many simple on-line algorithms (including the
algorithm presented in [6]), and found routing
problems for each algorithm that result in schedules that use
asymptotically more than
steps using a simple randomized algorithm provided that the underlying
network is leveled and has depth L. As a consequence, optimal
routing algorithms can be derived for most of the networks that are
commonly used for parallel computation. Unfortunately, it seems to be
difficult to extend this result to hold for all networks. In fact, we
have considered many simple on-line algorithms (including the
algorithm presented in [6]), and found routing
problems for each algorithm that result in schedules that use
asymptotically more than ![]() steps. Several of these
examples are included in Section 4.
steps. Several of these
examples are included in Section 4.
The results of this paper also have applications to job-shop
scheduling. In particular, consider a scheduling problem with jobs
![]() , and machines
, and machines ![]() , for which each
job must be performed on a specified sequence of machines. In our
application, we assume that each job occupies each machine that works
on it for a unit of time, and that no machine has to work on any job
more than once. Of course, the jobs correspond to packets, and the
machines correspond to edges in the packet routing problem. Hence, we
can define the dilation of the scheduling problem to be the
maximum number of machines that must work on any job, and the
congestion to be the maximum number of jobs that have to be run on
any machine. As a consequence of our packet routing result, we show
that any scheduling problem can be solved in
, for which each
job must be performed on a specified sequence of machines. In our
application, we assume that each job occupies each machine that works
on it for a unit of time, and that no machine has to work on any job
more than once. Of course, the jobs correspond to packets, and the
machines correspond to edges in the packet routing problem. Hence, we
can define the dilation of the scheduling problem to be the
maximum number of machines that must work on any job, and the
congestion to be the maximum number of jobs that have to be run on
any machine. As a consequence of our packet routing result, we show
that any scheduling problem can be solved in ![]() steps. In
addition, we will prove that there is a schedule for which each job
waits at most
steps. In
addition, we will prove that there is a schedule for which each job
waits at most ![]() steps before it starts running, and that each
job waits at most a constant number of steps in between consecutive
machines. The queue of jobs waiting for any machine will also always
be at most a constant. These results are optimal, and are substantially
better than previously known bounds for this problem
[4, 10].
steps before it starts running, and that each
job waits at most a constant number of steps in between consecutive
machines. The queue of jobs waiting for any machine will also always
be at most a constant. These results are optimal, and are substantially
better than previously known bounds for this problem
[4, 10].
Recently some results were proved in [11] for the more
general problem of job-shop scheduling where jobs are not assumed to
be unit length and a machine may have to work on the same job more
than once. They give randomized and deterministic algorithms that
produce schedules that are within a polylogarithmic factor of the
optimal length for the more general job-shop problem. However, it is
not known whether there exist schedules of length ![]() for this
problem.
for this
problem.
This paper also leaves open the question of whether or not there is an
on-line algorithm that can schedule any set of paths in ![]() steps
using constant-size queues. We suspect that finding such an algorithm
(if one exists) will be a challenging task. Our negative suspicions
are derived from the fact that we can construct counterexamples to
most of the simplest on-line algorithms. In other words, for several
natural on-line algorithms we can find paths for N packets for which
the algorithm will construct a schedule using asymptotically more than
steps
using constant-size queues. We suspect that finding such an algorithm
(if one exists) will be a challenging task. Our negative suspicions
are derived from the fact that we can construct counterexamples to
most of the simplest on-line algorithms. In other words, for several
natural on-line algorithms we can find paths for N packets for which
the algorithm will construct a schedule using asymptotically more than
![]() steps. Several of the counterexamples are
included in Section 4.
steps. Several of the counterexamples are
included in Section 4.