3.2 The main result

Proving that there is a schedule of length using constant-size queues is more difficult. Removing the factor in the length of the schedule seems to require delving into second-order terms in the probability calculations, and reducing the queue size to a constant mandates greater care in spreading delays out over the schedule.

Proof: To make the proof more modular, we bound the frame size and relative congestion after each step of the construction in lemmas. These lemmas and their proofs are included within the proof of the theorem. We assume without loss of generality that c=d, so that the bound on the length of the schedule is .

As before, the strategy is to make a succession of refinements to the greedy schedule, . The first refinement is special. It transforms into a schedule in which the relative congestion in each frame of size or more is at most 1. Thereafter, each refinement transforms a schedule with relative congestion at most in any frame of size or greater into a schedule with relative congestion at most in any frame of size or greater, where and , as shown in Figure 4. As well shall see, after j refinements, where , we obtain a schedule with constant relative congestion in every frame of size or greater, where is some constant. From it is straightforward to construct a schedule of length in which at most one packet traverses each edge of the network at each step, and at most a constant number of packets wait in each queue at each step.

  
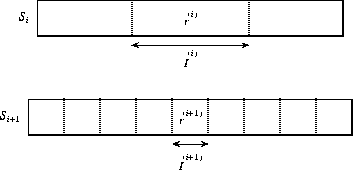
Figure 4: A refinement step. Each refinement transforms a schedule into a slightly longer schedule . The frame size is greatly reduced in , yet the relative congestion within a frame remains about the same, i.e., and .

At the start, the relative congestion in a d-frame of is at most 1. We begin by using Lemma 3.2 to produce a schedule of length in which the relative congestion is at most in any frame of size or greater.

Next, we repeatedly refine the schedule to reduce the frame size. As we shall see, the relative congestion and frame size for schedule are given by the recurrences

and

which have solutions and for some j, where .

We have not explicitly defined the values of and for which the recursion terminates. However, in several places in the proof that follows we implicitly use the fact that is sufficiently large that some inequality holds. The recursion terminates when the first of these inequalities fails to hold. When this happens, is bounded from above by some constant. Furthermore, independent of the depth of the recursion, is bounded from above by a constant.

Throughout the following lemmas we make references to quantities such as rI packets or time steps, when in fact rI and may not be integral. Rounding these quantities to integer values when necessary does not affect the correctness of the proof. For ease of exposition, we shall henceforth cease to consider the issue.

An important invariant that we maintain throughout the construction is that in schedule every packet waits at most once every steps. As a consequence, there is a constant such that a packet waits at most once every steps in , which implies both that the queues in cannot grow larger than a constant and that the total length of is . Schedule almost satisfies the requirement that at most one packet traverses each edge in each step. By simulating each step of in a constant number of steps we can meet this requirement with only a factor of 2 increase in the queue size and a constant factor increase in the running time.

The rest of the proof describes the refinement step in detail. For ease of notation, we use I and r in place of and .

The first step in the ith refinement is to break schedule into blocks of consecutive time steps. Each block is rescheduled independently.

For each block, each packet is assigned a delay chosen from 1 to I. We will use the Lovász Local Lemma to show that if the delays are chosen randomly, uniformly, and independently, then with non-zero probability the resulting schedule will have the properties that we want.

A packet that is assigned a delay of x must wait for x steps at the beginning of the block. In order maintain the invariant that in schedule every packet waits at most once every steps, the packet is not delayed for x consecutive steps at the beginning of the block, but instead a delay is inserted every I steps in the first xI steps of the block. A packet that is delayed x steps reaches its destination at the end of the block by step .

In order to independently reschedule the next block, the packets must reside in exactly the same queues at the end of the rescheduled block that they did at the end of the block of . Since some packets arrive early, they must be slowed down. Thus, if a packet is assigned delay x, then I-x delays are inserted in the last steps of the block, one every I steps. Since every packet experiences a total delay of I, the rescheduled block must have length .

Before the delays for schedule have been inserted, a packet is delayed at most once in each block of , provided that , which holds as long as I is larger than some constant. Prior to inserting each new delay into a block, we check if it is within I steps of the single old delay. If the new delay would be too close to the old delay, then it is simply not inserted. The loss of a single delay in a block has a negligible effect on the probability calculations in the lemmas that follow.

The following two lemmas are used several times in the proof of the theorem. Lemma 3.5 shows that if we can bound the relative congestion in frames of size T to 2T-1, then we can bound the relative congestion in all frames of size T or greater. Lemma 3.6 bounds the probability that too many packets use any particular edge g in any small frame in the center of a block after every packet has been delayed for a random number of steps at the beginning of the block.

 

Proof: Consider a frame of size , where . The first steps of the frame can be broken into T-frames. In each of these frames, at most RT packets use g. The remainder of the -frame consists of a single y-frame, where , in which at most Ry packets use g.

to .667emto .667em

 

Proof: We begin by computing an upper bound on the probability, , that more than packets use an edge g in a particular -frame. Since a packet may be delayed up to steps before the frame, any packet that used g in the -frame spanning the same steps in the block before the delays were inserted or in the steps before that frame may use g after the delays are inserted. Thus, there are at most packets that can use g in the frame. For each of these, the probability that the packet uses g in the frame after being delayed is at most , provided that the packet's path uses g at most once. Thus, the probability that more than packets use g in the frame is bounded by

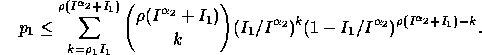
Let . We bound the series as follows. The expected number of packets that use g in the frame is . For and , is larger than the expectation, so the first term in the series is the largest, and there are at most terms. Applying the inequalities , for , and for 0 < b < a to this term, we have

For and , we can ensure that , for any constant by making constant large enough.

Next we need to bound the probability that more than packets use g in any -frame of the block. There are at most -frames. Thus . By making the constant large enough, we can ensure that , for any constant .

To bound the relative congestion in frames of size greater than , we appeal to Lemma 3.5. The calculations for frames of size through are similar to those for frames of size . There are at most frames of any one size, and frame sizes between and . By adjusting the constants as before, we can guarantee that the probability p that more than packets use g in any T-frame for T between and is at most for any constant .

to .667emto .667em

Lemma 3.7 shows that by inserting delays at the beginning and end of the block we can reduce the frame size in the center of the block while only slightly increasing the relative congestion. The bounds proved in Lemma 3.7 are shown in Figure 5.

 

Proof: The proof uses the Lovász Local Lemma. With each edge we associate a bad event. For edge g, a bad event occurs when more than packets use g in any T-frame for . To show that no bad event occurs, we need to bound both the dependence of the bad events and the probability that an individual bad event occurs.

We first bound the dependence, b. At most packets use an edge in the block. Each of these packets travels through at most other edges in the block. Furthermore, . Thus, a bad event depends on other bad events.

For any constant , we can bound the probability that a bad event occurs by by applying Lemma 3.6 with , , , , , and .

Since a bad event depends on only other bad events, we can make 4pb < 1 by making large enough. By the Lovász Local Lemma, there is some way of choosing the packet delays so that no bad event occurs.

to .667emto .667em

  
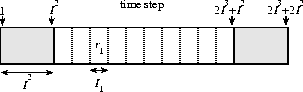
Figure 5: Bounds on frame size and relative congestion after inserting delays into . Here and .

Inserting delays into the schedule may increase the relative congestion in I-frames (or smaller frames) in the steps at the beginning and end of each block. In order to bound the relative congestion in small frames in these regions, we first move the block boundaries to the centers of the blocks, as shown in Figure 6. Now each block of size has a ``fuzzy'' region of size in its center. Lemma 3.8 shows that after moving the block boundaries, the relative congestion in any frame of size or larger in the block is at most . We will later insert more delays into the schedule and uses Lemmas 3.6 and 3.8 to help bound the relative congestion in small frames in the fuzzy region.

 

Proof: There are two cases to consider. First, consider a T-frame that lies entirely in the first half of a block, or entirely in the second half of a block. After the delays are inserted, a packet can use an edge in the T-frame only if it used the edge in some -frame in . Thus, at most packets can use an edge in the T-frame. For , the relative congestion is at most . Second, consider a T-frame that spans the center of the block. Suppose that the frame consists of steps before the center and after, so that . Then a packet can use an edge in the steps before the center only if it used the edge in one of the last steps before the end of a block in . Since may be less than I, we can't bound the relative congestion in the last steps at the end of a block. But we know that at most packets used the edge in the last steps, and hence in the last steps. Similarly, a packet can use an edge in the steps after the center only if it used an edge in one of the first steps of a block in . Hence, at most packets use the edge in the steps after the center. Since a total of at most packets use the edge, for the relative congestion is at most .

to .667emto .667em

To reduce the frame size in the fuzzy region, we assign a delay from 1 to to each packet. As before, we will use the Lovász Local Lemma to show that if the delays are chosen randomly, independently, and uniformly then with non-zero probability the resulting schedule has the properties we want. A packet with delay x waits once every steps in the steps before the fuzzy region. In addition, a packet with delay x waits once every steps in the last steps of the rescheduled block. Thus, every packet waits for a total of steps (except we do not insert a delay if it is within I steps of an old delay), and the rescheduled block now has size . Note that in the rescheduled block the width of the fuzzy region grows by time steps; it spans steps through .

  
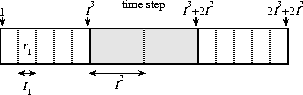
Figure 6: A block after recentering. The ``fuzzy region'' in the center of the block is shaded. The line bisecting the shaded region denotes the block boundary before recentering.

We now show that there is some way of inserting delays into the schedule before the fuzzy region that both reduces the frame size in the fuzzy region and does not increase either the frame size or the relative congestion before or after the fuzzy region by much.

Proof: The proof uses the Lovász Local Lemma as before. With each edge we associate a bad event. For edge g, a bad event occurs

1. if more than packets use g in any T-frame between steps and (i.e., in the fuzzy region), for any , or

2. if more than packets use g in any T-frame between steps and , for any , or

3. if more than packets use g in any T-frame between steps and , for any .

The calculation for the dependence b is the same as in Lemma 3.7. At most packets pass through each edge g, and each of these packets passes through at most other edges. Hence, .

To bound the probability that a bad event occurs, we consider the three cases separately, and sum their individual probabilities of occurrence.

Since no delays are inserted into the fuzzy region, we can use Lemma 3.6 to prove that for any constant , there is an such that the probability that more than packets use g in any T-frame between steps and , for any , is at most . We apply Lemma 3.6 with , , , , , , and .

Before the fuzzy region, the situation is more complex. By the kth step, , a packet with delay x has waited times. Thus, the delay of a packet at the kth step varies essentially uniformly from 0 to . For , or equivalently, , we can show that the relative congestion in any frame of size or greater has not increased much.

The probability that more than packets use an edge g in a particular -frame is given by

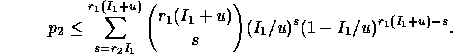
Using the same inequalities as in the proof of Lemma 3.6, we have

The calculations for frame of size through are similar. Thus for any constant , for , , and , the probability that more than packets use g in any T-frame between steps and , for any , is at most .

By symmetry, the probability that more than packets use g between steps and , for any , is also at most .

Thus, the probability that a bad event occurs for edge g is at most . Since the dependence is at most , by adjusting the constants and we can apply the Lovász Local Lemma.

to .667emto .667em

For steps 0 to , we use the following lemma to bound the frame size and relative congestion.

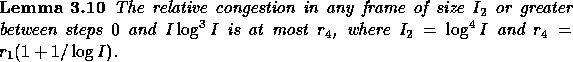
Proof: The proof is similar to that of Lemma 3.8.

to .667emto .667em

We have now completed our transformation of schedule into schedule . Let us review the relative congestion and frame sizes in the different parts of a block. Between steps 0 and , the relative congestion in any frame of size or greater is at most . Between this region and the fuzzy region, the relative congestion in any frame of size or greater is at most . In the fuzzy region, the relative congestion in any frame of size or greater is at most . After the fuzzy region, the relative congestion in any frame of size or greater is again , until step , where the relative congestion in any frame of size or greater is . These bounds are shown in Figure 7. Finally we must bound the relative congestion in frames that span the different parts of a block (or two different blocks). Since we have bound the relative congestion in blocks of size or greater, it is safe to say that in the the entire schedule the relative congestion in any frame of size or greater is at most .

to .667emto .667em

  
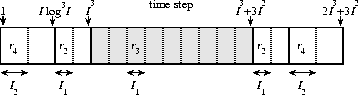
Figure 7: Final bounds on frame size and relative congestion. To reduce the frame size in the fuzzy regions, delays are inserted only outside the shaded region. Here , , , , and .