For simplicity, we have heretofore ignored the possibility of combining multiple packets with the same destination. In many routing applications, there is a simple rule that allows two packets with the same destination to be combined to form a single packet, should they meet at a node. For example, one of the packets may be discarded, or the data carried by the two packets may be added together. Combining is used in the emulation of concurrent-read concurrent-write parallel random-access machines [29] and distributed random-access machines [23].
If the congestion is to remain a lower bound when combining is allowed, then its definition must be modified slightly. The new congestion of an edge is the number of different destinations for which at least one packet's path uses the edge. Thus, several packets with the same destination contribute at most one to the congestion of an edge.
In order to efficiently combine packets, we will use a random hash function to give all of the packets with the same destination the same rank. Since ties in rank are broken according to destination, a node will not send a packet in one of its queues unless it is sure that no other packet for the same destination will arrive later in another queue. Thus, at most one packet for each destination traverses an edge.
We assign ranks using the universal hash function [7]
which maps a destination 
to a rank in
with k-wise independence. Here P is a prime number
greater than the total number of destinations, and the coefficients
are chosen at random. We show below that it suffices to
choose 
. The random coefficients use 
random bits. In most applications, only 
-wise
independence is needed and the number of possible
different destinations is at most polynomial in N, so the hash
function requires only 
bits of randomness.
In the proof of Theorem 2.9, the ranks of the w packets in a delay sequence were chosen independently, i.e., with w-wise independence. In order to use a hash function with m-wise independence, where m may be much smaller than w, we need the following lemma, which shows that in any delay sequence there are smaller subsequences of many different sizes.
Proof:
Suppose that an 
-delay sequence occurs.
Divide the packet sequence 
into 
contiguous
subsequences such that each subsequence has at least 
packets. This also partitions the delay path into
subpaths. Let 
denote the length of the ith subpath and let
denote the range of ranks for the ith subsequence, i.e., 
is the difference between the largest rank in subsequence i and the
largest rank in subsequence i-1. We know that there must be fewer
than 
segments with 
, since 
.
Furthermore there must be fewer than 
segments satisfying
, since 
. Thus there must exist some
segment for which 
and 
.
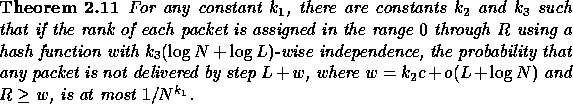
Proof:
The proof is similar to that of Theorem 2.9.
If some packet is not delivered by step L+w then by
Lemma 2.5 an 
-delay sequence
occurs. By Lemma 2.10, for any 
a
-delay sequence also occurs.
The hash function will be 
-wise independent.
We will show that for the right choices of w and 
, it is
unlikely that any such sequence occurs.
The number of different 
-delay
sequences is bounded as follows. A delay path starts at node on some
packet's path. Thus, there at most 
starting points for the
path. At each node on the path, there are at most 
choices
for the next node on the path. Thus, the total number of ways to
choose the path is at most 
. The
number of ways of choosing 
switches on the path is at most
. The number of
ways of choosing 
packets that pass through those switches
is at most 
. The number of ways of choosing
the ranks for the packets is at most 
since there are R choices for the rank of the
first packet, and the ranks of the other 
differ from
the first by at most 
.
If the ranks of the packets are chosen using a 
-wise
independent hash function, then the probability that any particular
delay sequence occurs is at most 
. Thus, the
probability that any delay sequence occurs is at most
Using the inequality 
to bound
, and 
to
bound 
by 
, and 
, 
,
and 
to bound
by
, our upper bound becomes
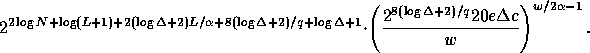
Removing constants so that we can better understand the expression, we have
If 
, then for any constant 
there are
constants 
and 
such that for 
and 
, the probability is at most 
.
If 
then for any 
there is a 
such that
and 
and for 
, and 
, the
probability is at most 
.
