In this section we apply the scheduling algorithm from
Section 2 to route N packets in 
steps on an N-node butterfly using constant size queues. We
essentially duplicate the result of Ranade [29], but the
proof is simpler.
In a butterfly network, each node has a distinct label 
, where l is its level and r is its row. In an
n-input butterfly, l is an integer between 0 and 
, and
r is a 
-bit binary number. The nodes on level 0 and 
are called the inputs and outputs, respectively. Thus, an
n-input butterfly has 
nodes. For 
, a
node labeled 
is connected to nodes 
and 
, where 
denotes r with the lth bit complemented. An 8-input butterfly
network is illustrated in Figure 3. Sometimes the
input and output nodes in each row are identified as the same node.
In this case the number of nodes is 
. The butterfly has
several natural recursive decompositions. For example, removing the
nodes on level 0 (or 
and their incident edges leaves two
-input subbutterflies.
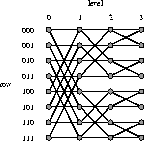
Figure 3: An 8-input butterfly
network. Each node has a level number between 0 and 3, and a
3-bit row number. A node on level l in row r is connected to
the nodes on level l+1 in rows r and 
, where where
denotes r with the lth bit complemented.
Proof:
Routing is performed on a logical network consisting of 
levels. The first 
levels of the logical network are linear
arrays. The packets originate in these arrays, one to a node. Levels
through 
form a butterfly network. Levels 
through 
consist of a butterfly with its levels reversed.
The last 
levels are again linear arrays. Each packet has its
destination in one of the arrays spanning levels 
to 
. Packets with the same destination are combined. The butterfly
simulates each step of this logical network in a constant number of
steps. Paths for the packets are selected using Valiant's paradigm;
each packet travels to a random intermediate destination on level
before moving on to its final destination. This strategy
ensures that with high probability, say at least 
, where
is a constant, the congestion is 
. Since the paths
are chosen independently of the ranks for the packets, the scheduling
algorithm can treat the paths as if they were fixed. Assuming that
the paths have congestion 
, by Theorem 2.9
the scheduling algorithm delivers all of the packets in 
steps, with high probability, say at least 
. Thus, the
probability that either the congestion is too large or that the
scheduling algorithm takes too long to deliver the packets is at most
.
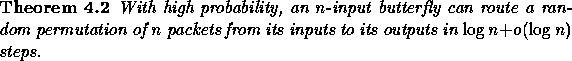
Proof:
If each input sends a single packet, the congestion will be
, with high probability. Given paths with
congestion 
, by Theorem 2.9
the delay is 
, with high probability.