In this section we construct a class of networks that are
area-universal in the sense that a network in the class with N
nodes has area 
and can, with high probability, simulate in
steps each step of any network of area 
.
The networks are based on the fat-trees of Greenberg and Leiserson
[10] and the simulation uses the packet routing
algorithm from Section 2.
Leiserson was the first to display a class of networks that could
efficiently simulate any other network of the same area or volume. In
[21] he showed that a fat-tree of area 
can
simulate in 
bit-steps each bit-step of any network of
area 
. (In the bit model an edge can transmit a single
bit in each time step. All of the algorithms in this paper are
described in terms of the packet model, in which an edge can transmit
a packet of at least 
bits in one step.) Leiserson's
simulation used an off-line routing algorithm for fat-trees. On-line
routing algorithms were later developed by Greenberg and Leiserson
[10].
A fat-tree network is shown in Figure 5. Its underlying
structure is a complete 4-ary tree. Each edge in the 4-ary tree
corresponds to a pair of oppositely directed groups of edges called
channels. The channel directed from the leaves to the root is
called an up channel; the other is called a down channel. The
capacity of a channel C, 
, is the number of edges
In the channel. We call the tree ``fat'' because the capacities of
the channels grow by a factor of 2 at every level. A fat-tree of
height m has 
nodes at the root and
leaves.
It will prove useful to label the nodes at the top and bottom of
each channel. Let the level of a node be its distance from the
leaves. Suppose a channel C connects 
nodes at level l with 
nodes at level
l+1. Give the nodes at level l labels 0 through 
and
the nodes at level l+1 labels 0 through 
. Then
node k at level l is connected to nodes k and 
at
level l+1. The following lemma relates the labels of the nodes
on a packet's path from a leaf to the root.
The simplest way to route packets in a leveled fashion on a fat-tree
is to route every packet all of the way up to the root before routing
it down to its destination. The problem with this strategy is that it
may cause unnecessary congestion at the root. For example, suppose
that every leaf wants to send a single packet to its sibling. If
these packets are sent to the root, then 
packets will pass
through each channel at the root. On the other hand, if each packet
goes up just one level before turning around, then at most one packet
will pass through any channel in the entire network. Thus, we will
route every packet from its origin to its destination along a path
that passes through as few channels as possible.
For a set Q of packets to be delivered between the leaves of the
fat-tree, we define the load of Q on a channel C,
, to be the number of different destinations of packets in
Q for which at least one packet must pass through C. (A packet
must pass through C only if every path from the packet's origin to
its destination passes through the C.) Note that even if many
packets with the same destination must pass through a channel, that
destination contributes at most one to the load of the channel. The
routing algorithm will combine all packets with the same destination
that attempt to pass through the channel. We define the load
factor of Q on C, 
, to be the ratio of the load
of Q on C to the capacity of C, 
The load factor 
on the entire
network is simply the maximum load factor on any channel 
The load factor is a lower bound on the the
number of steps required to deliver Q. We shall sometimes write
to denote 
when the set of packets to be
delivered is clear from the context.
In a leveled fat-tree a node at the top of an up channel at
level l is connected to itself at the top of the corresponding down
channel by a linear chain of nodes of length 
. A packet
may only make a transition from an up channel to a down channel by
traversing a chain. Thus all shortest paths between leaves in a
leveled fat-tree have length 2m. Note that the load of a set of
packets on a channel of the leveled fat-tree is identical to the load
on the corresponding channel in the fat-tree.
The path that a packet for destination x takes through a leveled fat-tree is determined by the m-universal hash function [7]
where P is a prime number larger than the number of possible
different destinations, and the 
are chosen at
random off-line. A packet with destination x follows up channels
along the unique shortest path to the node labeled 
at the
root until it can reach x without using any more up channels. It
then crosses over to a down channel via a chain, and follows down
channels to x. Note that a packet only passes through a channel if
all paths from its origin to its destination pass through that
channel. Also, all packets with destination x that pass through
channel C pass through node 
at the top of C and through node 
at the bottom of C.
The following lemma shows that we can use the scheduling algorithm from Section 2 to route packets in a fat-tree.
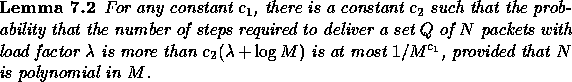
Proof:
The paths of the packets are first randomized using
the universal hash function 
. With high probability, the
resulting congestion is 
. Each packet
travels a distance of 
. The packets are then
scheduled using the algorithm from
Section 2.
Let us now consider the VLSI area requirements [34] of
fat-trees. A fat-tree with root capacity M and 
nodes has a layout with area 
that is obtained
by embedding the fat-tree in the tree of meshes [15].
The nodes of the tree of meshes in this layout are separated by a
distance of 
in both the horizontal and vertical directions.
Thus, the 
space for the chain associated with each
node in the leveled fat-tree can be allocated without increasing
the asymptotic area of the layout. (In fact, it is possible to attach
a chain of size 
to each fat-tree node without increasing
the area by more than a constant factor.) The leaves of the fat-tree
are separated in the layout from each other by a distance of 
in each direction. We can improve the density of nodes without
increasing the asymptotic area of the layout by connecting a 
mesh of nodes to each leaf. The resulting network
has 
nodes and area 
.
The N-node network in this class has root capacity
, 
leaves, and area
.
The following theorem shows that this class of networks is area-universal.
Proof:
The nodes of network B are mapped to the
nodes of the area-universal network U off-line using a recursive
decomposition technique as in [21]. In each step, an
edge of B is simulated by routing packets between the nodes that it
connects. At each level of the recursion at most 
edges connect the nodes mapped below a channel C with
the rest of the network. This property of the mapping ensures that
the load factor of each set of packets used in the simulation of B
is at most 
. At the bottom of the decomposition tree, a
region of the layout of B is mapped to
each leaf of the fat-tree. The 
mesh
connected to the leaf in U simulates this region of B with 
slowdown using a mesh routing algorithm such as the one in
Section 3.
The study of fat-tree routing algorithms that perform combining was
motivated in part by an abstraction of the volume and area-universal
networks called the distributed random-access machine (DRAM). A host
of conservative algorithms for tree and graph problems for the
exclusive-read exclusive-write (EREW) DRAM are presented in
[22]. Recently we discovered conservative
concurrent-read concurrent-write (CRCW) algorithms that require fewer
steps for some of these problems [23]. Until now, however,
no efficient fat-tree routing algorithms that perform combining were
known. The 
step routing algorithm presented
here fills the void.
Only slight modifications to the area-universal fat-tree are necessary
to make it volume universal [10]. The underlying
structure of the volume-universal fat-tree is a complete 8-ary tree.
Instead of doubling at each level, the channel capacities increase by
a factor of 4. The tree has m levels, root capacity 
,
and 
leaves. The nodes at the top of a channel
at level l are labeled 0 through 
. Node k at level l
is connected to nodes k, 
, 
, and
at level l+1. A layout with volume 
for the fat-tree can be obtained by embedding it
in the three-dimensional tree of meshes. As before, a chain
of size 
can be attached to each node of the fat-tree
without increasing the asymptotic layout area and the density of
nodes can be improved by connecting a 
mesh to each leaf.
The simulation scheme in this section can also be used to simulate
shared-bus networks. In a shared-bus network, an edge is allowed to
connect more than two nodes. If several nodes attempt to send
packets on the same edge in the same step, then the packets are
combined using some simple rule to form a single packet. Combining
is assumed to require a single step, regardless of the number of
packets combined or the rule used. Because the fat-tree routing
algorithm is capable of combining, it is no more difficult for the
fat-tree to simulate shared-bus networks than to simulate
point-to-point networks (i.e., networks in which each edge connects a
pair of nodes). The simulation is optimal because a
point-to-point network may require 
steps to simulate
one step of a shared-bus network. Previously, no fat-tree routing
algorithms were capable of combining packets to the same destination.
As a consequence, no scheme for simulating shared-bus networks was
known. A network that can simulate in 
steps each step of any
shared-bus network area of equal area was presented in
[24]. However, the connections in that network are
not fixed, but instead nodes communicate via reconfigurable
buses.
